Моделирование процедуры вычисления спектральных характеристик методом фильтрации с использованием гетеродина;

Белорусский Государственный Университет

Факультет Радиофизики и Компьютерных технологий

Лабораторная работа № 3

Изучение измерительных информационных систем для анализа стохастических процессов (на примере анализатора СК4-72)

Вариант 5

Выполнил

5 курс 5 группа

Минск 2013

Задачи:

1.  Смоделировать процедуру вычисления спектральных характеристик методом фильтрации с использованием гетеродина;

2.  Изучить функциональную схему и органы управления анализатора с временной компрессией СК4-72.

.

Важные параметры в моделировании процессов следующие:

f_s = 2250 Гц;                          частота сигнала(случай кратной t сигнала)

F_d = 22500 Гц;                     частота дискретизации  

N = 10000-1 , 1000-1;                                  число отсчетов сигнала

Δt = 1/F_d =4.4 * 10^-5 с;     интервал дискретизации

T = N * Δt =0.0044 с;           длительность реализации  

Δf = F_d / N =227 Гц;             разрешение по частоте;

F_d /2 =11250 Гц;                   полоса анализа сигнала.

1.Метод периодограмм

Использование различных окон для оценки амплитуды гармонической составляющей

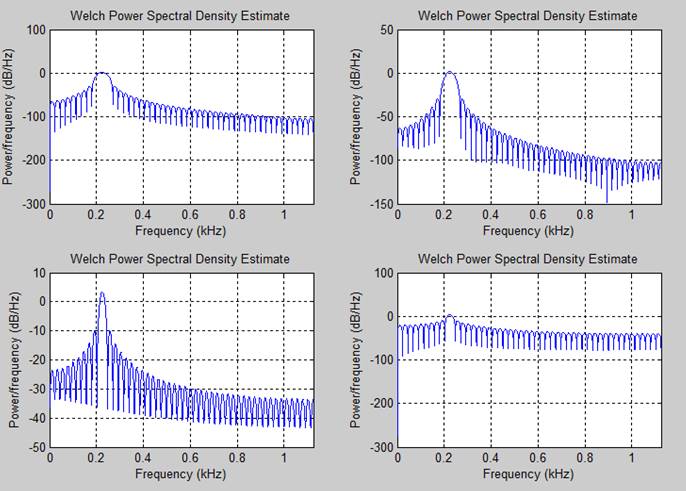
Использовались окна Хэмминга и прямоугольное окно различных длин.  (1 строка – Хемминг, 1 столбец - количество отсчетов дающее разрешение попадающее на fs

2. Моделирование методов оценки спектра

Стационарный сигнал:

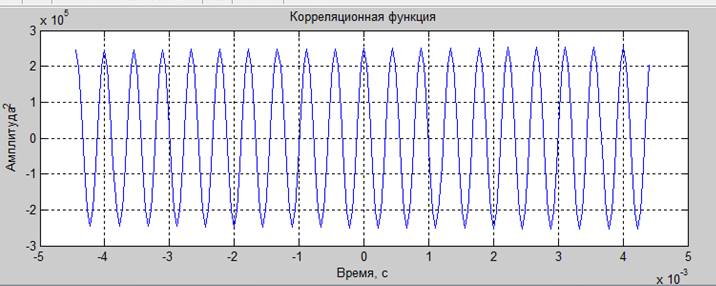
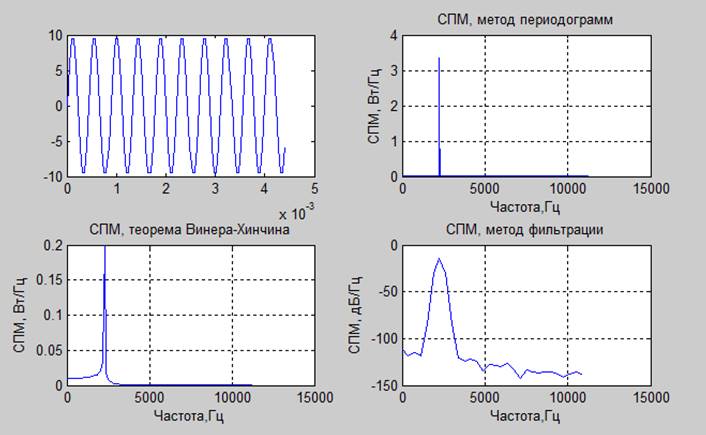
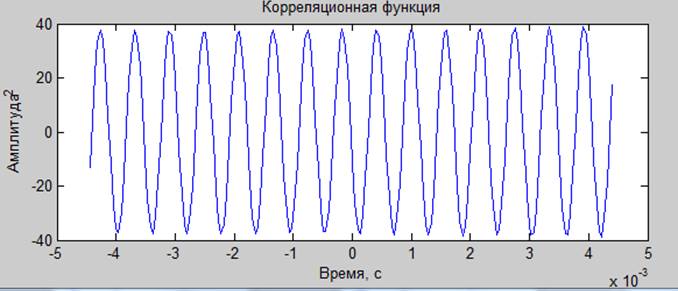
Гармонический сигнал:

мощность:                                                                      50.01000;

мощность из оценки методом периодограмм:           49.9756344; мощность из оценки по теореме Винера-Хинчина     58.17419; методом фильтрации:                                                     128.2672

Свип сигнал:

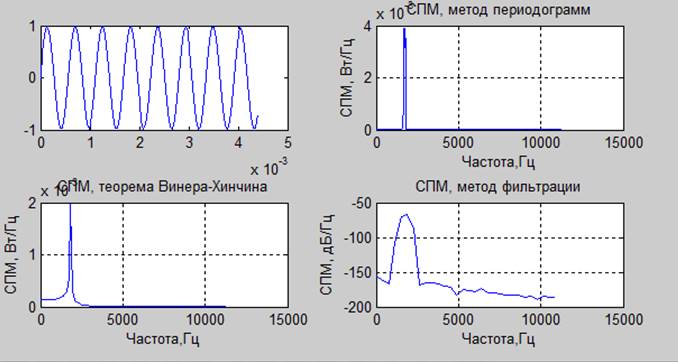
Вывод: Наиболее узкие пики дает метод периодограмм и метод основанный на теореме Винера-Хинчина, хотя при этом он дает ошибку в суммарной мощности из-за сложности получения точной спектральной оценки. Наиболее точные данные по суммарной мощности дает метод периодограмм. Наихудшие оценки мощности получились у метода фильтрации так как получился широкий пик спектра.

Код программы

Файл lab3.m

clc;

%  Commom lab paramaters

fs = 2250;       % частота сигнала (гармоническая составляющая);

fd = 22500;      % частота дискретизации   = 1/ ?t; (из варианта )

N = 10000 -1;        % число отсчетов сигнала;    (кратно периоду)

dt = 1/fd;       % – интервал дискретизации

tBeg = 0;

tEnd = N * dt;   % – длина реализации   = N * ?t, (интервал наблюдения);

df = fd/N;       % разрешение по частоте   = Fd / N;

fd/2;            % - полоса анализа сигнала

averageCoefficient = 30;

t = (tBeg : dt : tEnd);  % формирование времени отсчетов

format long

signalAmplitude = 10; 

signalNoize = 20; % в децибеллах

noizeAmplitude = signalAmplitude / 10^(signalNoize/20);

% Гармонический сигнал

harmonySignal = signalAmplitude * sin (2 * pi * fs * t);

T=10;

%непериодический - свип

K=-fs*5/T*2;% за время Т частота пройдет через 0 и опять востановится

swipSignal=sin(fs*5*t+K/2*(t.^2));

partToDraw = N;

if(partToDraw > N )  

partToDraw = N;

end;

n1 = 99;

n2 = 100;

% windowHanning1 = hanning(n1);  % количество отсчетов для окна дающее разрешение попадающее на fs

% subplot(2,2,1)

% pwelch(harmonySignal, windowHanning1, 0, partToDraw, fs);

%

% windowHanning2 = hanning(n2);  % количество отсчетов для окна когда fs попадет между отсчетами

% subplot(2,2,2)

% pwelch(harmonySignal, windowHanning2, 0, partToDraw, fs);

%

%

% windowOnes1 = rectwin(n1);  % количество отсчетов для окна дающее разрешение попадающее на fs

% subplot(2,2,3)

% pwelch(harmonySignal, windowOnes1, 0, partToDraw, fs);

%

% windowOnes2 = rectwin(n2);  % количество отсчетов для окна когда fs попадет между отсчетами

% subplot(2,2,4)

% pwelch(harmonySignal, windowOnes2, 0, partToDraw, fs);

% lab3Process(harmonySignal, fs ,fd, N, dt, tBeg, tEnd, df, t,% 'гармонический сигнал')

lab3Process(swipSignal, fs ,fd, N, dt, tBeg, tEnd, df, t, 'свип сигнал')

файл lab3Process

function [  ] = lab3Process( signal, fs ,fd, N, dt, tBeg, tEnd, df, t, signalName)

n1 = 99;

n2 = 100;

corr=xcorr(signal);

%Расчет  корреляционных характеристик

step = -tEnd/100 : 1 / fd : tEnd/100;

plot(step(1,:),corr(1,4900:5099));

title('Корреляционная функция');

xlabel('Время, с');

ylabel(' Амплитуда^2');

figure;

subplot(2,2,1)

plot(t(1:100), signal(1:100))

% Оценка методом периодограмм

[powspec freq]=pwelch(signal,[],[],[],fd);

subplot(2,2,2)

plot(freq,powspec);

title('СПМ, метод периодограмм');

xlabel('Частота,Гц');

ylabel('СПМ, Вт/Гц');

grid on;

% Оценка по теореме Винера-Хинчина

[corr lags]=xcorr(signal(1:n2),'unbiased');

powercor=fft(corr)/(2*n2-1)/fd*length(corr);

subplot(2,2,3);

plot(0:1/2/0.0044:fd/2,abs(real(powercor(1:n2))));

title('СПМ, теорема Винера-Хинчина');

xlabel('Частота,Гц');

ylabel('СПМ, Вт/Гц');

grid on;

% оценка методом фильтрации

nchunks=30;

chunksize=int32(N/nchunks);

frequencyBand=fd/2/nchunks;

powerFilter=zeros(1,nchunks);

for j=1:nchunks

chunk=signal((1:chunksize)+(j-1)*chunksize);

heterodin=cos(2*pi*(j-1)*frequencyBand*t(1:chunksize));

signalTmp=chunk.*heterodin;

power=pwelch(signalTmp,[],[],[],fd);

freqbandsize=floor(length(power)/nchunks);

powerFilter(j)=sum(power(1:freqbandsize));

end;

subplot(2,2,4);

plot(0:frequencyBand:fd/2-frequencyBand,10*log(powerFilter));

title('СПМ, метод фильтрации');

xlabel('Частота,Гц');

ylabel('СПМ, дБ/Гц');

grid on;

signalFFT = fft(signal, [], 2)/N;

signalFFT = signalFFT(:, 1:floor(N)/2 + 1);

partTime = N / fd;

partFrequency = 1 / partTime;

transform = signalFFT .* conj(signalFFT) / partFrequency;

frequency=(0 : floor(tEnd * fd) / 2) * partFrequency;

spectrumPower = sum(2 * transform,2)*(1/tEnd)           %Мощность сигналов по спектральным характеристикам

periodogramm = sum(powspec)*fd/2/length(powspec)                 % периодограммы

vinerHinch = sum(abs(real(powercor(1:n2))))*fd/2/n2    %винера -хинча

filtration = sum(powerFilter)*frequencyBand                          %фильтрации

end