Исследование стохастических процессов. Смесь гармонического сигнала и шума. Математическое ожидание сгенерированного процесса

                   Белорусский государственный университет

Факультет радиофизики и компьютерных технологий

Лабораторная работа № 2

Исследование стохастических процессов

Выполнили:

Студенты 5 курса

(3гр)

(4гр)

Вариант 6

2013

Цель работы: изучить стационарные и нестационарные случайные процессы. При исследовании необходимо решить следующее задачи:

· синтезировать модели АМ, ЧМ- и ФМ-сигналов со случайными параметрами модуляции. Вычислить спектральные характеристики.

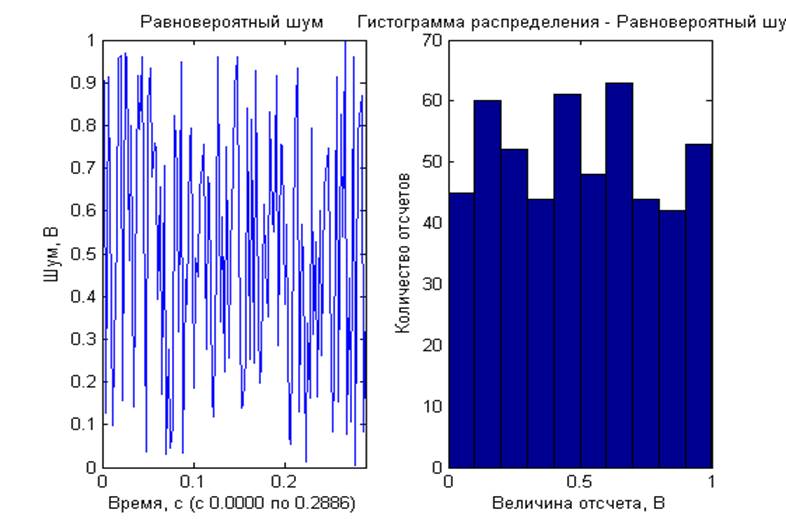
· синтезировать равновероятный шум. Построить гистограмму распределения.

Вычислить спектральные характеристики.

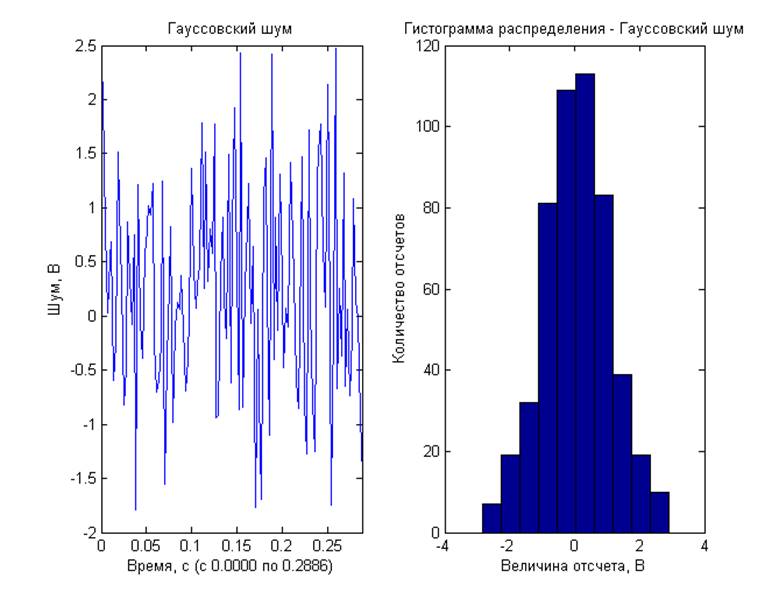
· синтезировать ≪белый≫ гауссовский шум. Построить гистограмму распределения.

Вычислить спектральные характеристики.

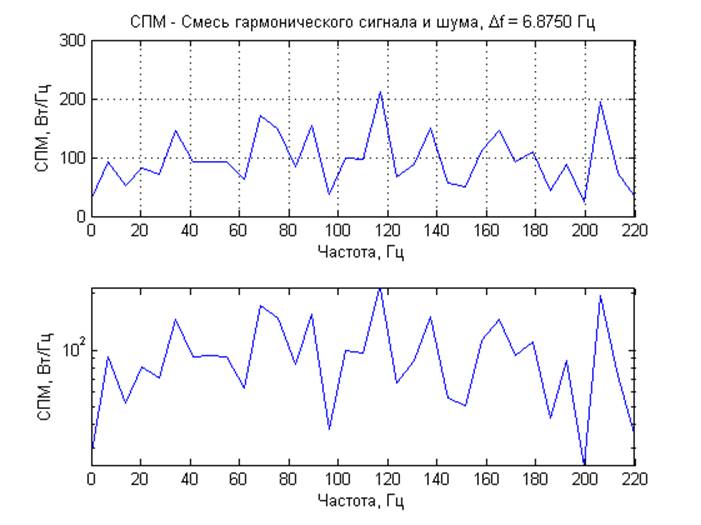
· Синтезировать смесь гармонического сигнала и шума. Задать отношение сигнал/шум [-40,-20,0,+20 dB]. Построить гистограмму распределения. Вычислить спектральные характеристики в линейном и логарифмическом масштабах.

Ход выполнения:

Частота дискретизации Fd = 440 Гц, количество отсчетов N = 512, в качестве сигнала используется напряжение на сопротивлении 1 Ом.

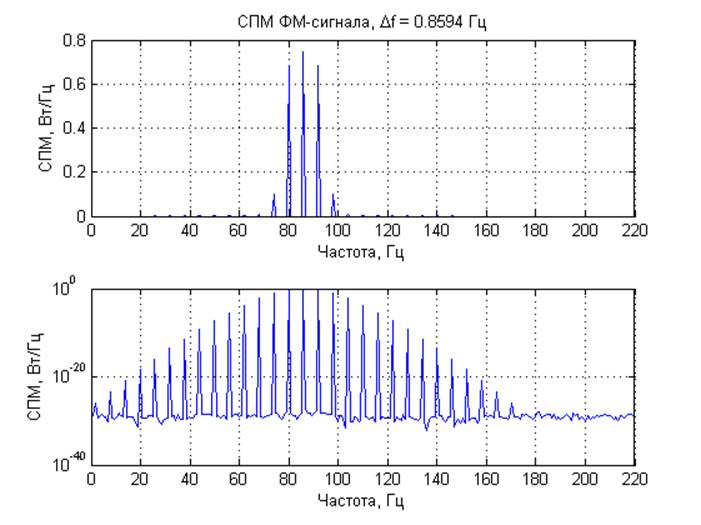
1) Модели АМ, ЧМ- и ФМ-сигналов, частота модулируемого сигнала Fs = 85.9375Гц;  частота модулирующего сигнала для АМ Fam = 2.5781 Гц, для ФМ и ЧМ – Fm = 6.015 Гц; индекс амплитудной модуляции m = 0.4; индекс фазовой модуляции Θ = 1.4; девиация частоты ΔΩ = 12; амплитуда модулируемого сигнала A = 2, модулирующего – Am = 1.

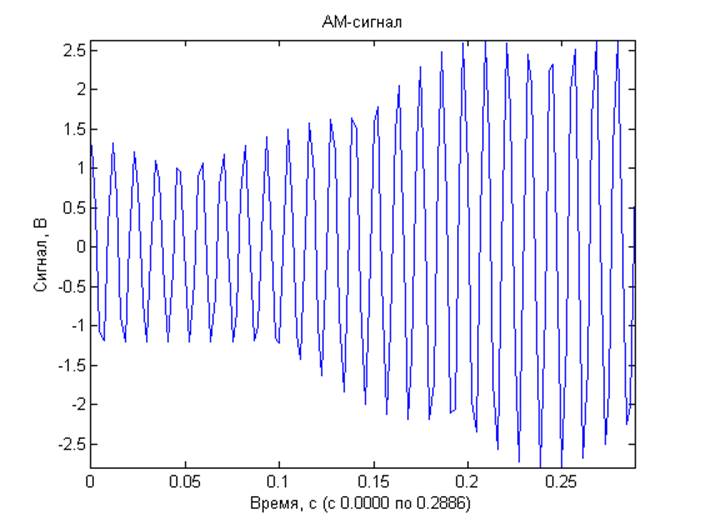
Математическое ожидание сгенерированного процесса: - 0.0000 В.

Дисперсия сгенерированного процесса: 2.1642 В2.

Суммарная мощность (по постоянной и переменной составляющим)

сгенерированного процесса: 2.1642 Вт.

Средняя мощность, вычисленная по СПМ: 2.1600 Вт.

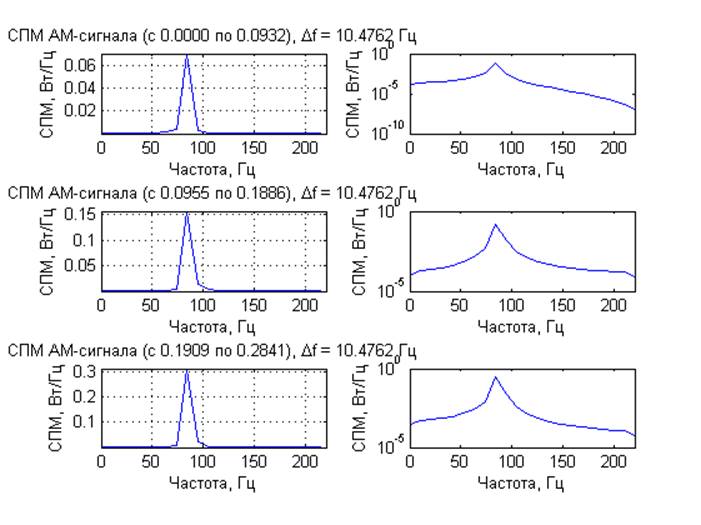
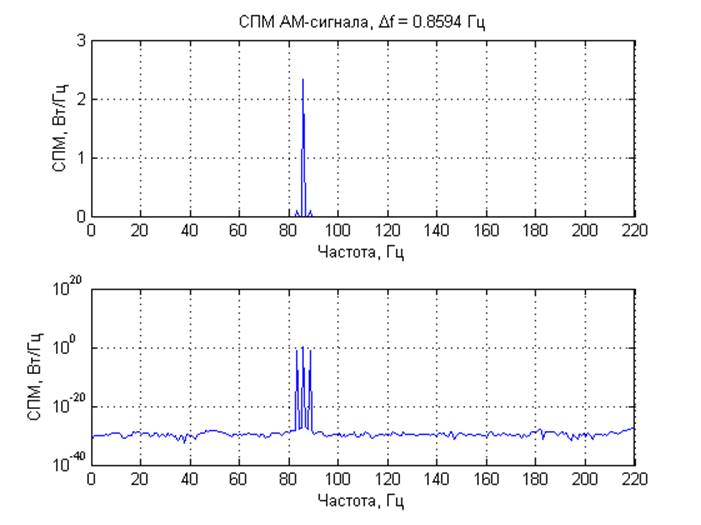
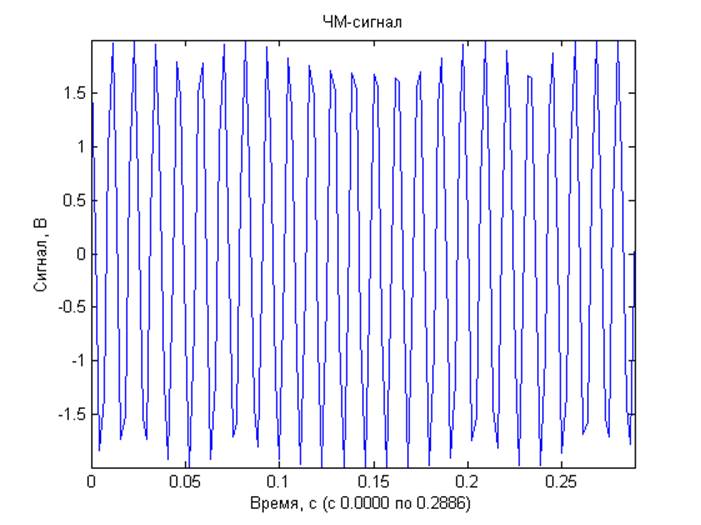
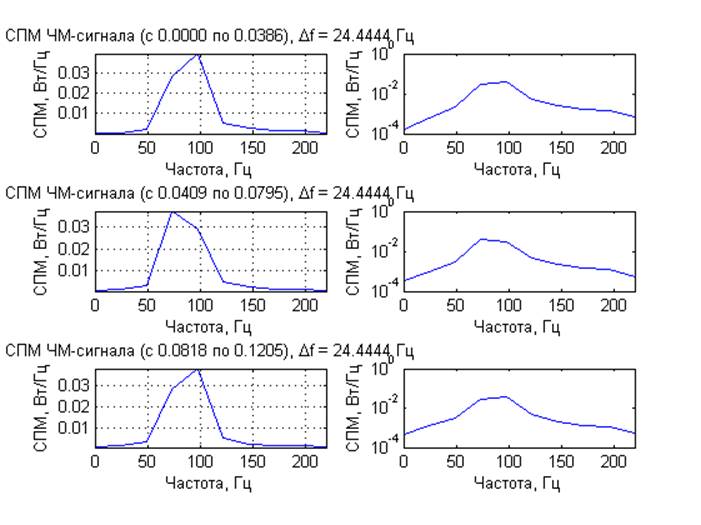
Математическое ожидание сгенерированного процесса: -0.0000 В.

Дисперсия сгенерированного процесса: 2.0039 В2.

Суммарная мощность (по постоянной и переменной составляющим)

сгенерированного процесса: 2.0039 Вт.

Средняя мощность, вычисленная по СПМ: 2.0000 Вт.

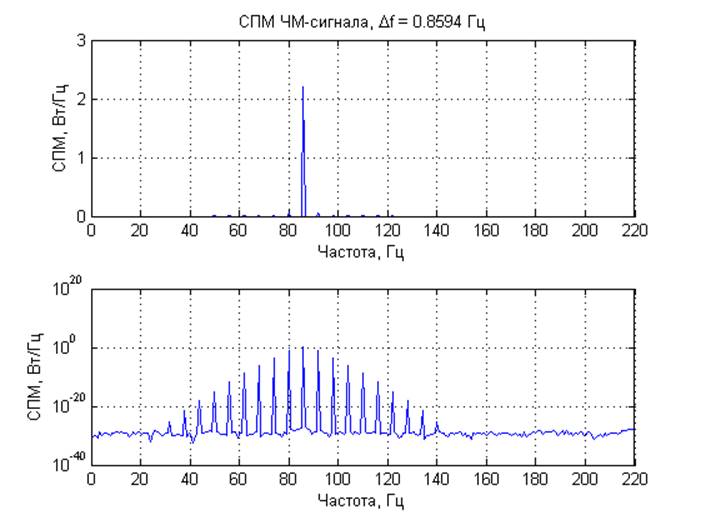
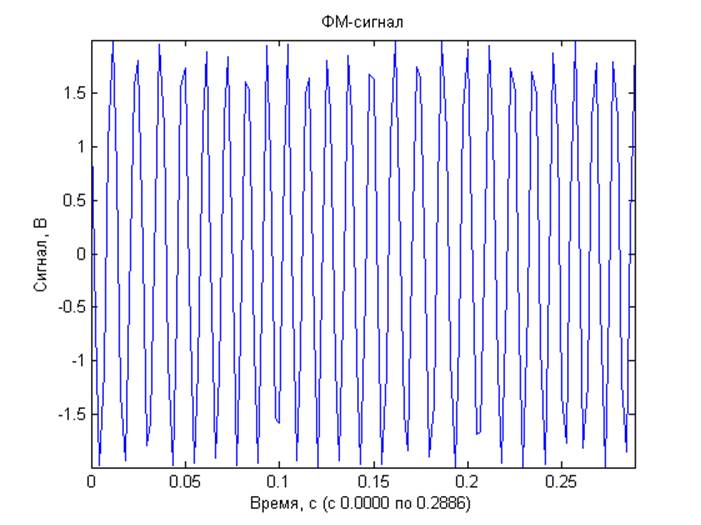
Математическое ожидание сгенерированного процесса: -0.0000 В.

Дисперсия сгенерированного процесса: 2.0039 В2.

Суммарная мощность (по постоянной и переменной составляющим)

сгенерированного процесса: 2.0039 Вт.

Средняя мощность, вычисленная по СПМ: 2.0000 Вт.

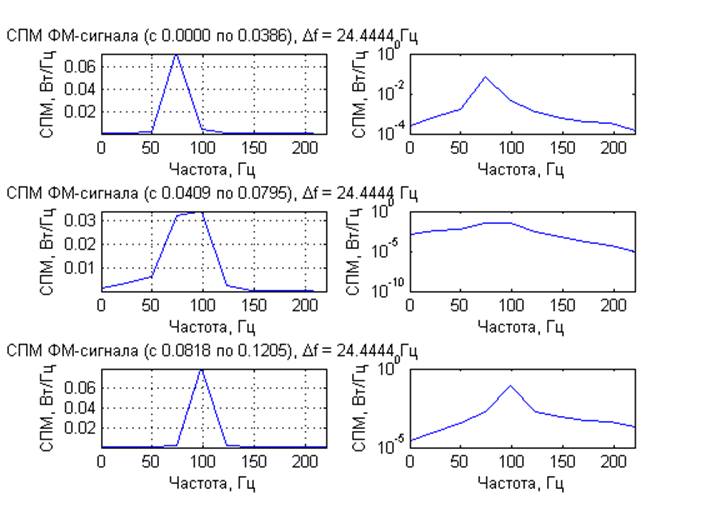
2) Равновероятный шум

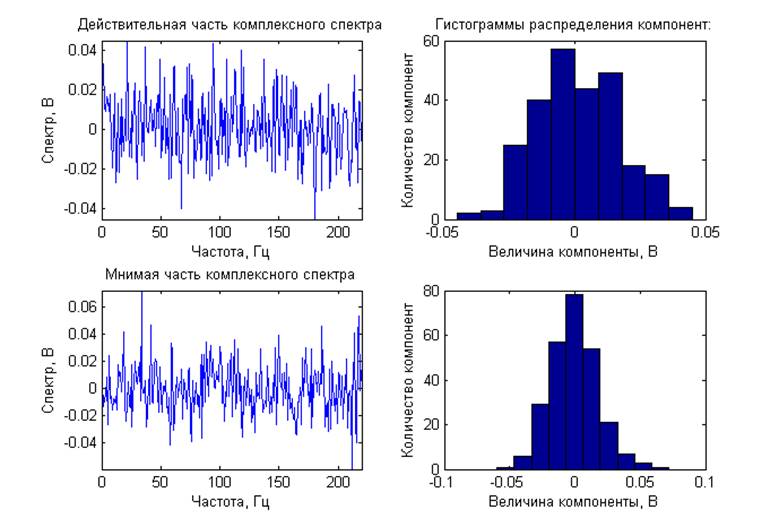
Спектральные характеристики (по отдельной реализации без усреднения, центрированный сигнал):

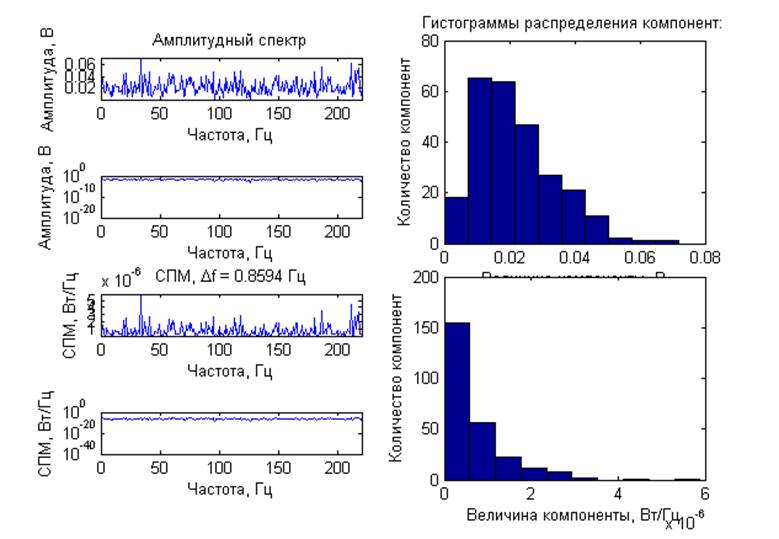
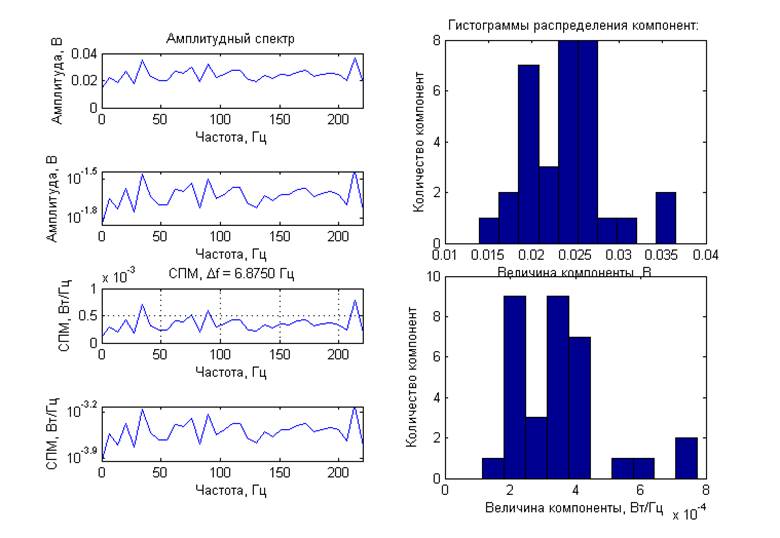
Спектральные характеристики (с усреднением, центрированный сигнал):

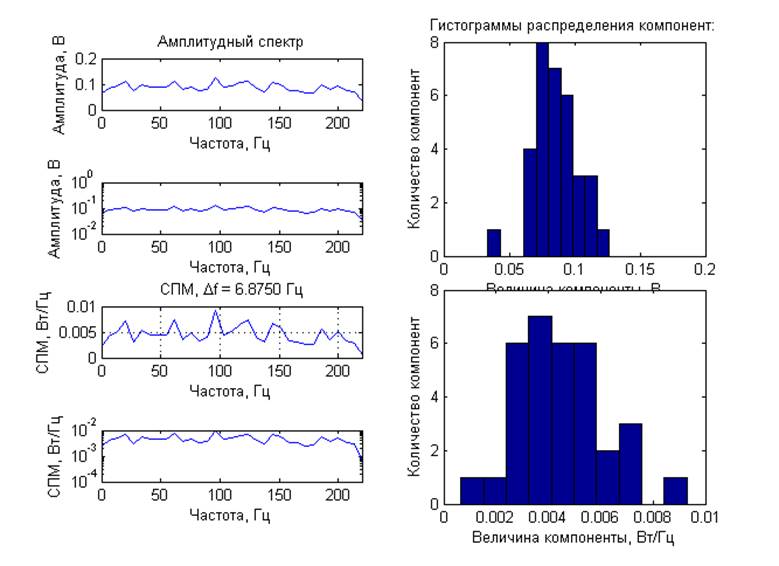
3) «Белый» гауссовский шум

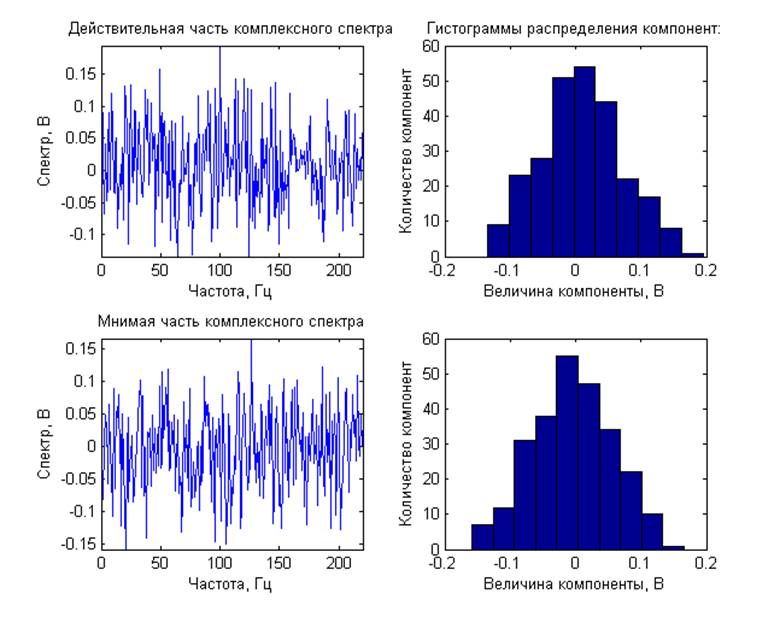
Спектральные характеристики (по отдельной реализации без усреднения, центрированный сигнал):

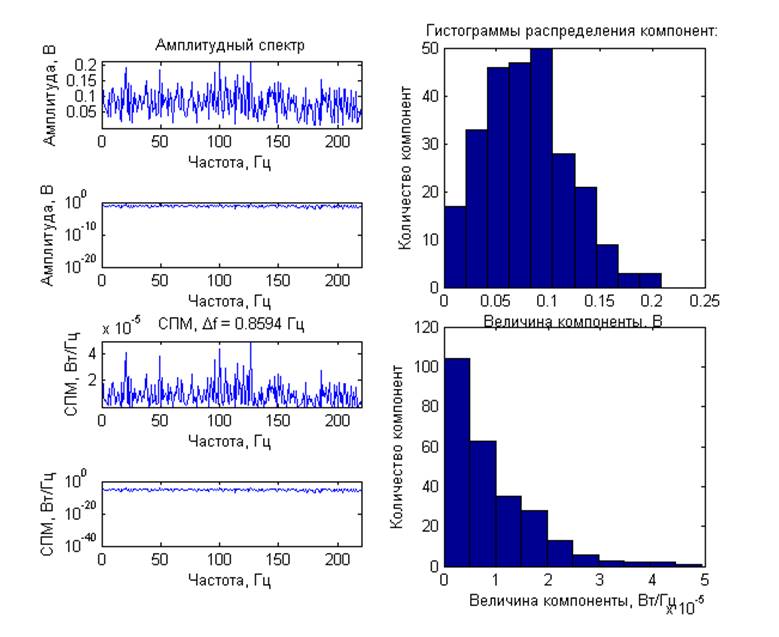
Спектральные характеристики (с усреднением, центрированный сигнал):

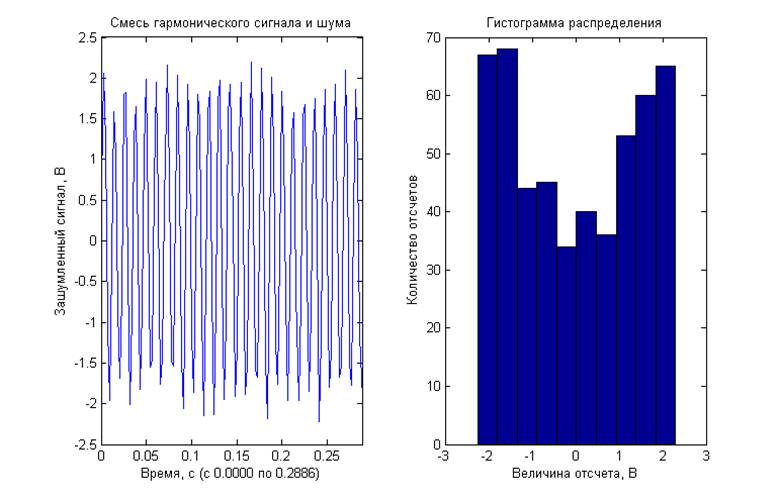
4) Смесь гармонического сигнала и шума (амплитуда гармонического сигнала 2 В)

Отношение сигнал/шум 20 дБ

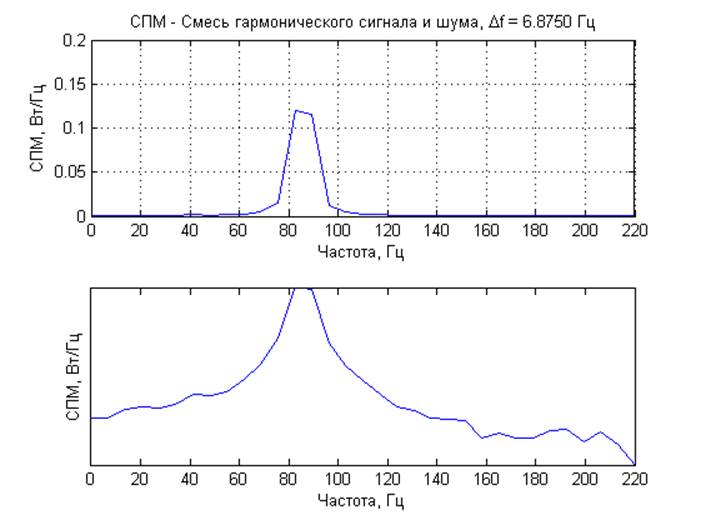
Отношение сигнал/шум 0 дБ

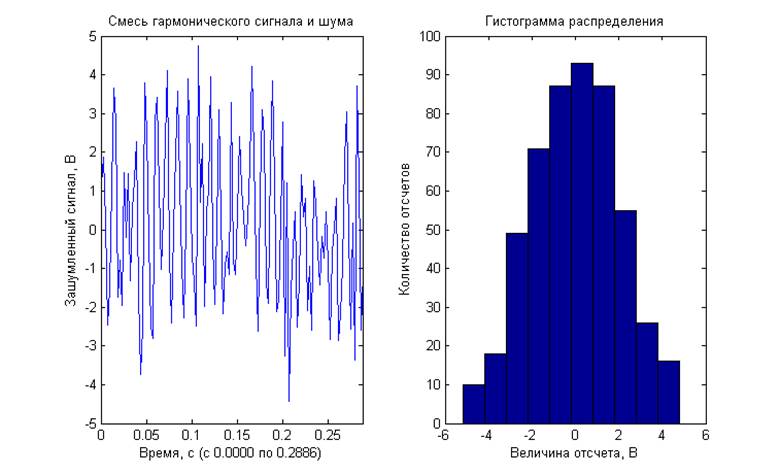
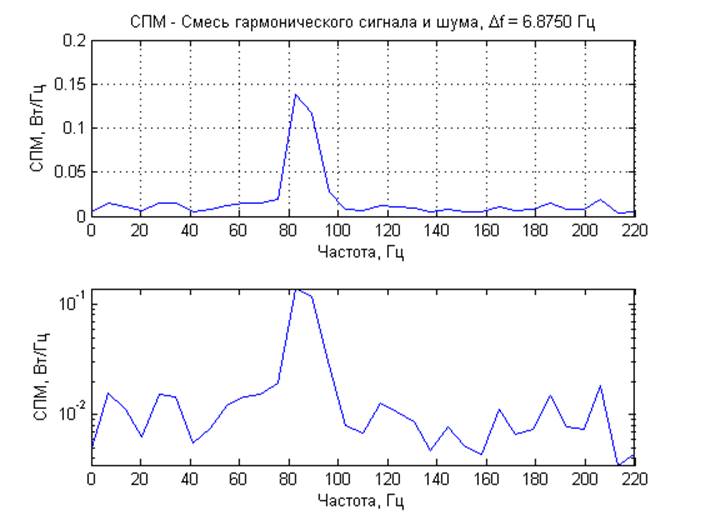
Отношение сигнал/шум -20 дБ

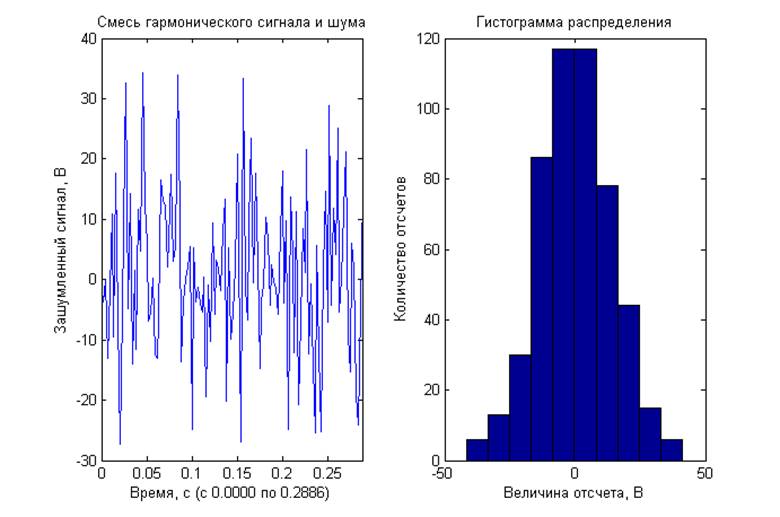
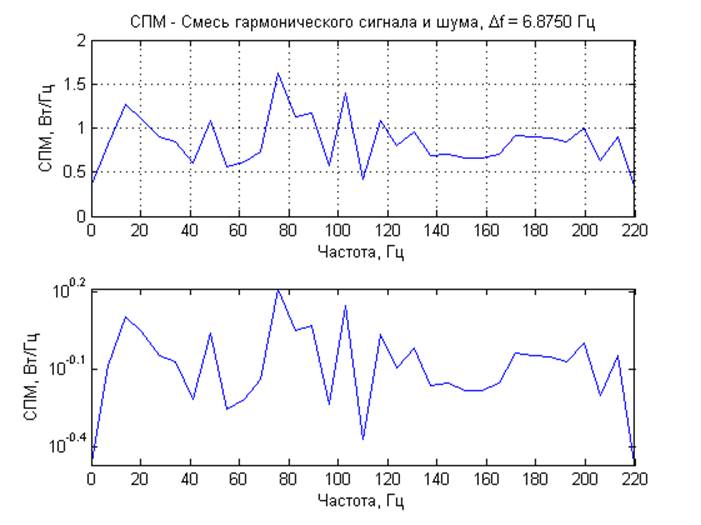
Отношение сигнал/шум -40 дБ

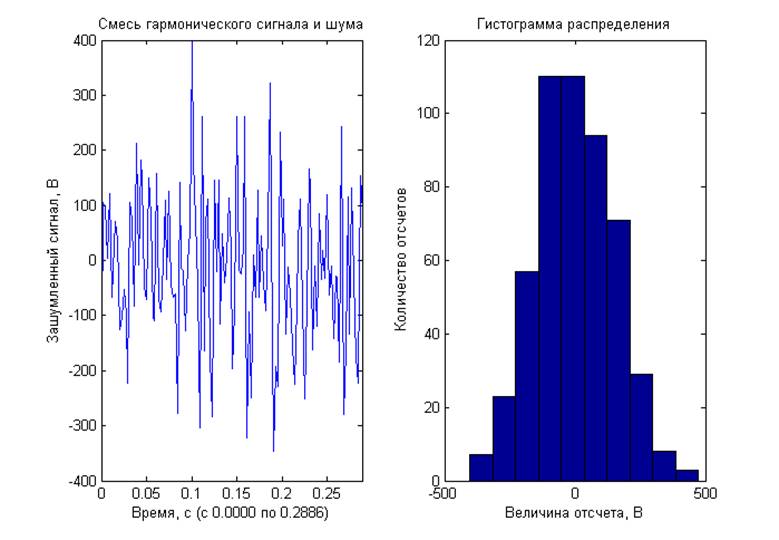
Выводы: Для модулированных процессов получены кратковременные спектры с несколькими задержками по времени от начала реализации исходного процесса, длительность временного окна 1/4 периода модулирующего сигнала Они демонстрируют нестационарную природу модулированных процессов. ЧМ и ФМ-сигналы имеют схожие спектральные характеристики. Для шумовых процессов получены спектральные характеристики. При вычислении ДПФ из-за суммирования помноженных на комплексные экспоненты отсчетов шума, представляющих собой случайную величину, по центральной предельной теореме получаем нормальное распределение компонент комплексного спектра. Для амплитудного спектра – распределение Рэлея, для СПМ –

хи-квадрат с 2 степенями свободы. Так же получены амплитудный спектр и СПМ со статистическим усреднением. Для смеси гармонического сигнала и шума при отношение сигнал/шум 0 и 20 дБ на графике спектральных характеристик отчетливо виден пик на частоте гармонического сигнала. При -20 и -40 дБ определить частоту гармонического сигнала на фоне шума не возможно.

Код MatLab

Файл Main

clc;

clear all;

%Флаги выводимой информации

flagAM = 0;

flagFM = 0;

flagPhM = 0;

flagUniformNoise = 0;

flagGaussNoise = 0;

flagNoisySig = 1;

%Входные данные

fd = 440; %частота дискретизации

N = 2^9; %число отсчетов

SNR = -40; %отношение сигнал/шум

deltaf = fd/N; %разрешение по частоте

fs = deltaf*60; %частота сигнала

fam = deltaf*3; %частота модулирующего сигнала для АМ

fm = deltaf*7; %частота модулирующего сигнала для УМ

m = 0.4; %индекс амплитудной модуляции

teta = 1.4; %индекс фазовой модуляции

deltaOmega = 12; %девиация частоты

A = 2; %амплитуда сигнала

t = (0:N - 1)/fd; %вектор времени

%АМ-сигнал

if flagAM == 1

name = 'АМ-сигнал';

sigAM = A*(1 + m*cos(2*pi*fam*t + 3/4*pi)).*cos(2*pi*fs*t);

analysisSigMod(sigAM, fam, fd, name);

end;

%ЧМ-сигнал

if flagFM == 1

sigFM = A*cos(2*pi*fs*t + deltaOmega/(2*pi*fm)*sin(2*pi*fm*t + 5/16*pi));

name = 'ЧМ-сигнал';

analysisSigMod(sigFM, fm, fd, name);

end;

%ФМ-сигнал

if flagPhM == 1

sigPhM = A*cos(2*pi*fs*t + teta*cos(2*pi*fm*t + 5/16*pi));

name = 'ФМ-сигнал';

analysisSigMod(sigPhM, fm, fd, name);

end;

%Равновероятный шум

if flagUniformNoise == 1

name = 'Равновероятный шум';

noise = rand(1, N);

analysisNoise(noise, fd, name);

end;

%Гауссовский шум

if flagGaussNoise == 1

name = 'Гауссовский шум';

noise = randn(1, N);

analysisNoise(noise, fd, name);

end;

%Смесь гармонического сигнала и шума

if flagNoisySig == 1

name = 'Смесь гармонического сигнала и шума';

noisySig = A*sin(2*pi*fs*t) + sqrt((A^2/2)/10^(SNR/10))*randn(1, N);

noisySig = noisySig - mean(noisySig);

%Вывод зашумленного сигнала

figure('Name', name);

subplot(1, 2, 1);

plot(t, noisySig);

title(name);

xlabel(sprintf('Время, с (c %2.4f по %2.4f)', t(1), t(floor(end/4))));

ylabel('Зашумленный сигнал, В');

xlim([t(1) t(floor(end/4))])

subplot(1, 2, 2);

hist(noisySig);

title('Гистограмма распределения');

xlabel('Величина отсчета, В');

ylabel('Количество отсчетов');