Исследование стохастических процессов. Важные параметры в моделировании процессов

Белорусский Государственный Университет

Факультет Радиофизики и Компьютерных технологий

Лабораторная работа № 2

Исследование стохастических процессов

Вариант 5

Выполнил

5 курс 5 группа

Минск 2012

Цель работы:

. изучить стационарные и нестационарные случайные процессы. При исследовании необходимо решить следующее задачи:

1.  синтезировать модели АМ, ЧМ- и ФМ-сигналов со случайными параметрами модуляции. Вычислить спектральные характеристики.

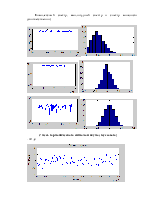
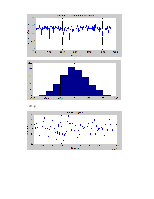
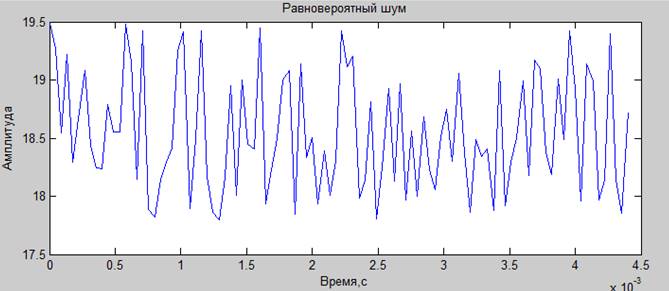
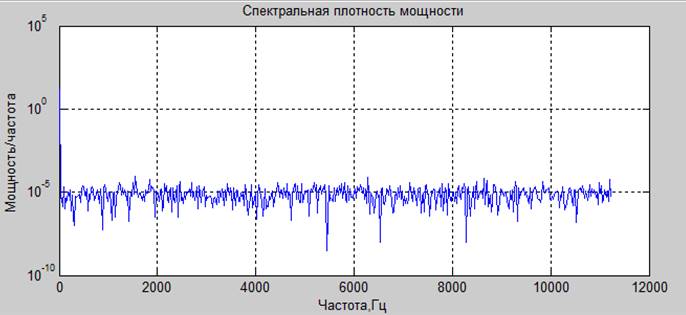
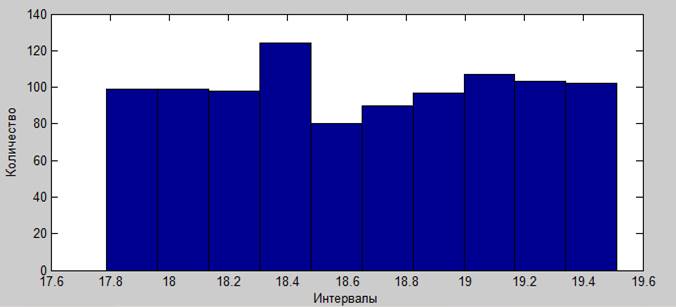
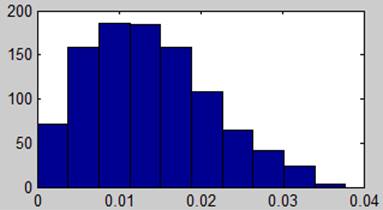
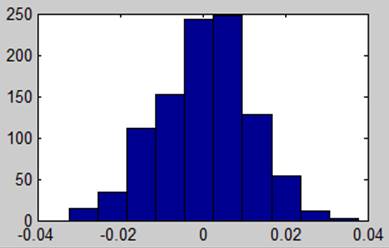
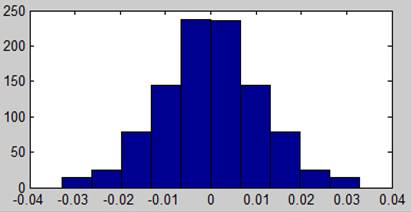
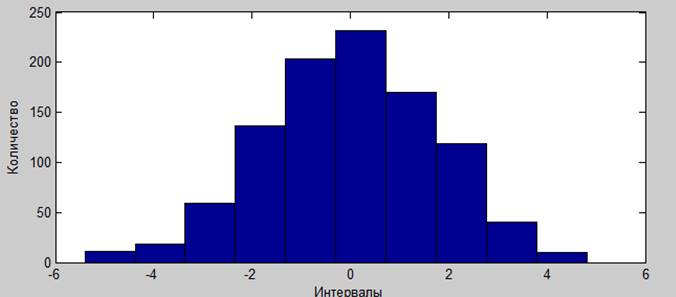
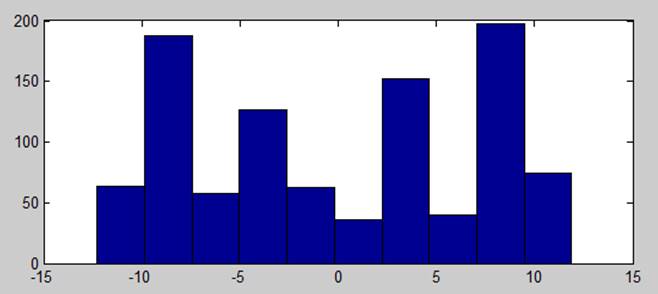
2.  синтезировать равновероятный шум. Построить гистограмму распределения. Вычислить спектральные характеристики.

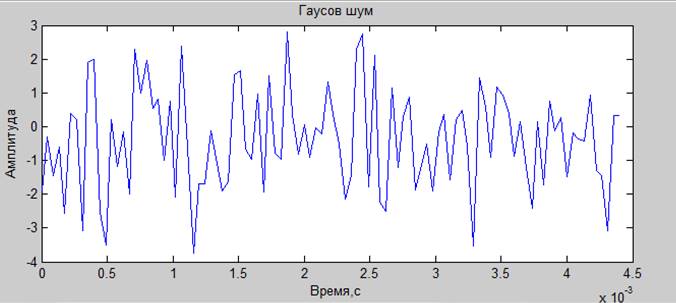
3.  синтезировать «белый» гауссовский шум. Построить гистограмму распределения. Вычислить спектральные характеристики.

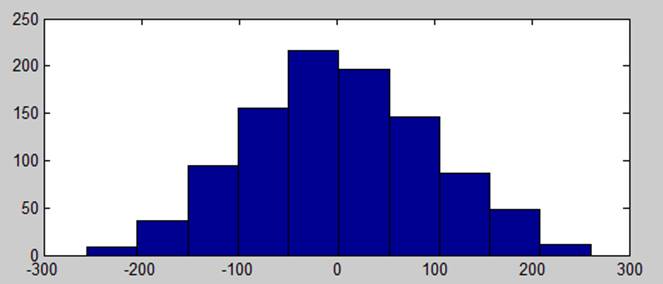
4.  Синтезировать смесь гармонического сигнала и шума. Задать отношение сигнал/шум [-40,-20,0,+20 dB]. Построить гистограмму распределения. Вычислить спектральные характеристики в линейном и логарифмическом масштабах.

.

Важные параметры в моделировании процессов следующие:

fs = 2250;        частота несущего сигнала (гармоническая составляющая);

fi = 1125;         частота информационного сигнала

F_d = 22500 Гц;                     частота дискретизации  

N = 1000-1;                                     число отсчетов сигнала

Δt = 1/F_d =4.4 * 10^-5 с;     интервал дискретизации

T = N * Δt =0.0044 с;           длительность реализации  

Δf = F_d / N ;                разрешение по частоте;

F_d /2 =11250 Гц;                   полоса анализа сигнала.

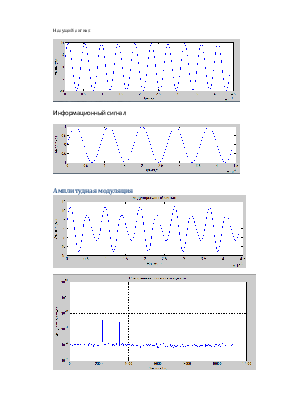
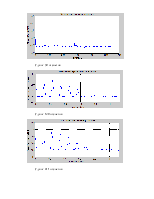
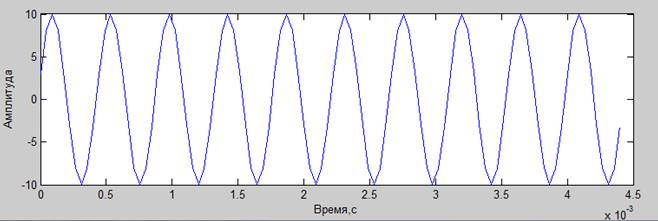
Несущий сигнал

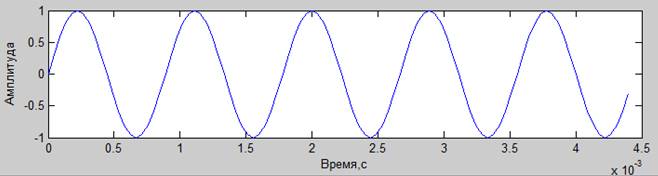
Информационный сигнал

Амплитудная модуляция

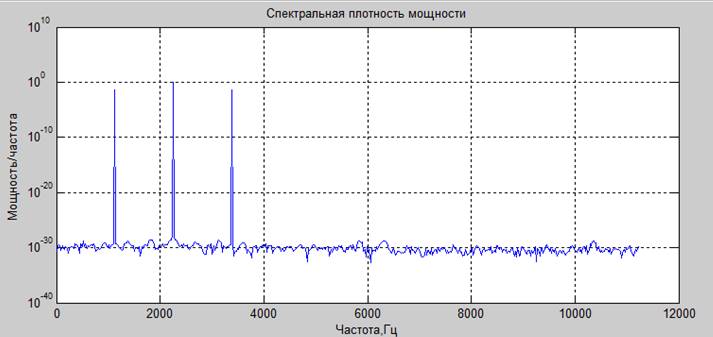
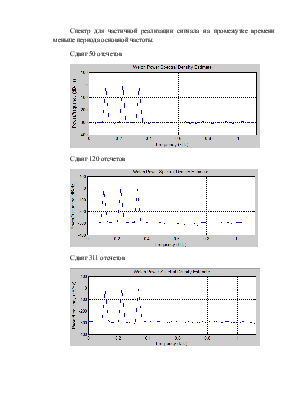
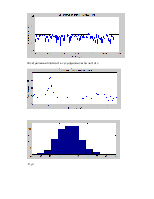
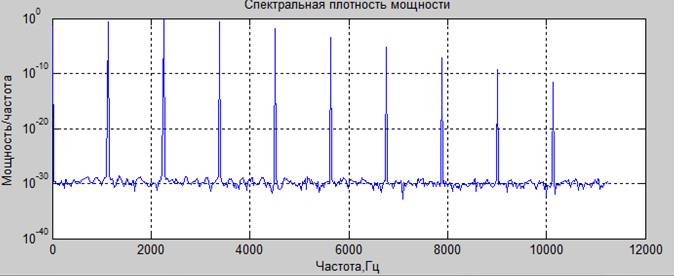
Спектр для частичной реализации сигнала на промежутке времени меньше периода основной частоты.

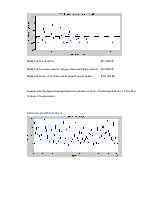
Сдвиг 50 отсчетов

Сдвиг 120 отсчетов

Сдвиг 311 отсчетов

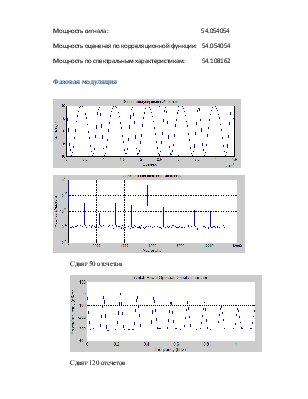
Мощность сигнала:                                                              54.054054

Мощность оцененая по корреляционной функции:   54.054054

Мощность по спектральным характеристикам:           54.108162

Фазовая модуляция

Сдвиг 50 отсчетов

Сдвиг 120 отсчетов

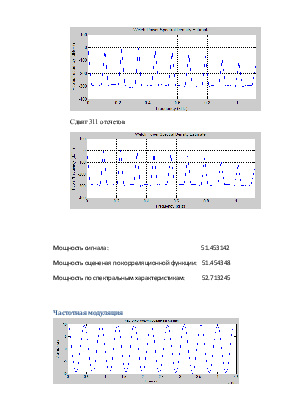
Сдвиг 311 отсчетов

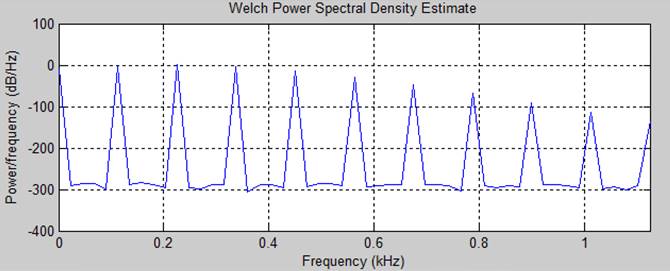
Мощность сигнала:                                                              51.453142

Мощность оцененая по корреляционной функции:   51.454348

Мощность по спектральным характеристикам:           52.713245

Частотная модуляция

Сдвиг 50 отсчетов

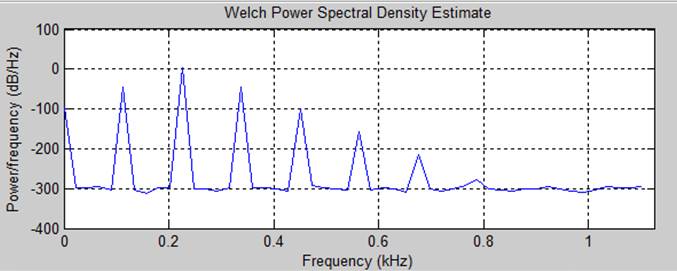
Сдвиг 120 отсчетов

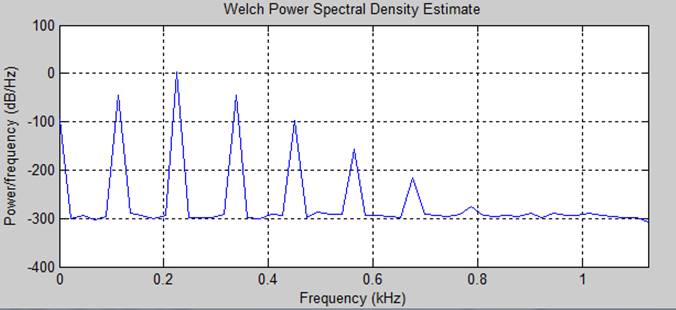
Сдвиг 311 отсчетов

Мощность сигнала:                                                              50.05005

Мощность оцененая по корреляционной функции:   50.05005

Мощность по спектральным характеристикам:           50.100150

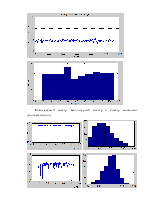
Вывод. Амплитудная модуляция гармонического сигнала добавляет в спектр только 2 гармоники.

Равновероятный шум.

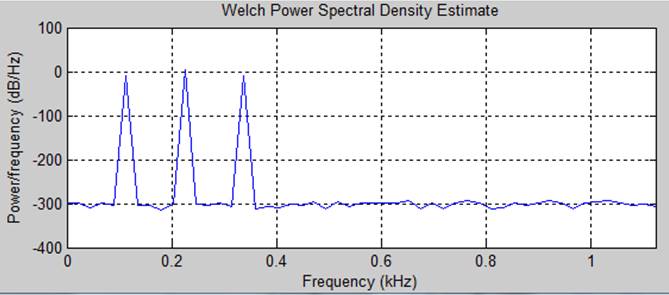
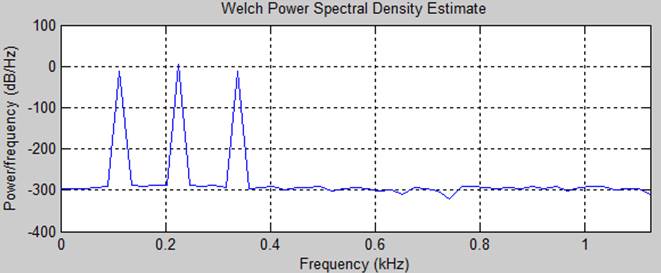
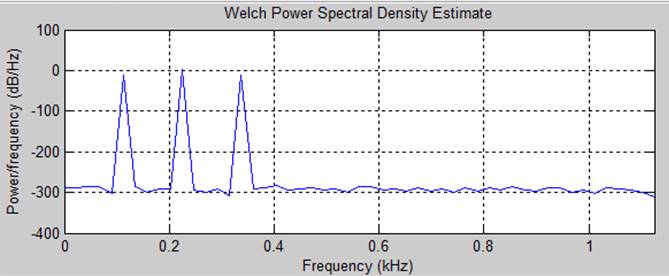
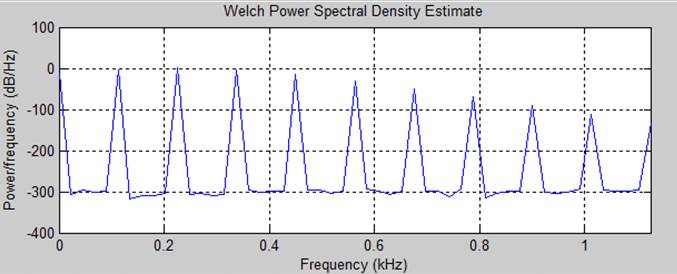
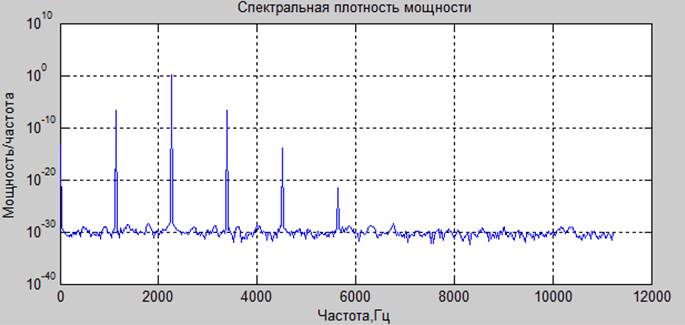
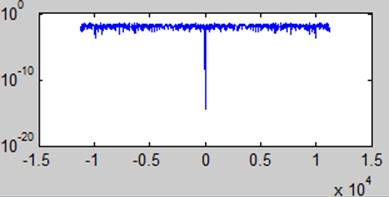
Комплексный спектр, амплитудный спектр и спектр мощности (соответственно)

Гауссов шум

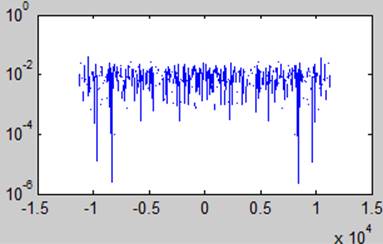
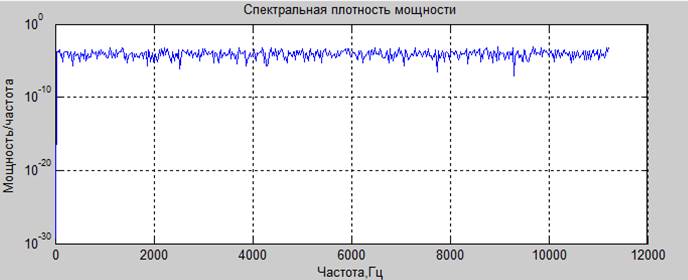
Комплексный спектр, амплитудный спектр и спектр мощности (соответственно)

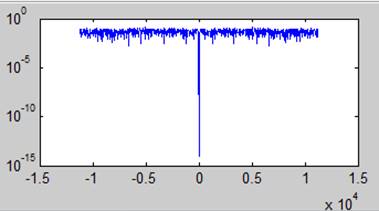
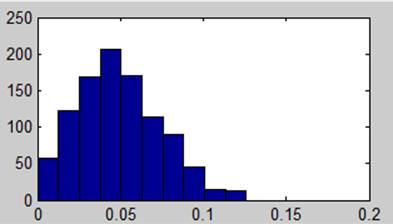
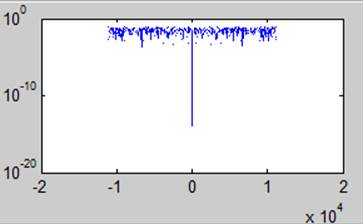
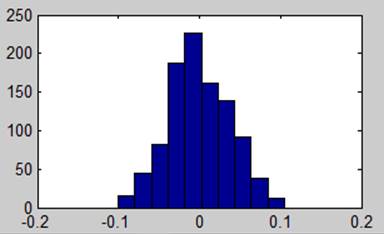
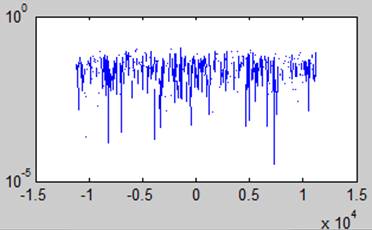
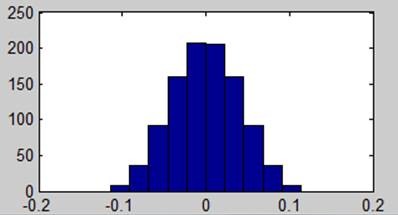
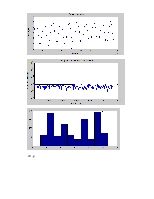
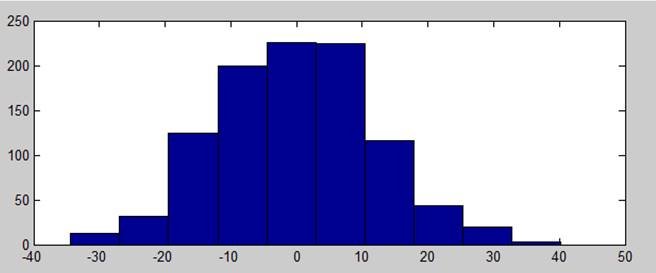
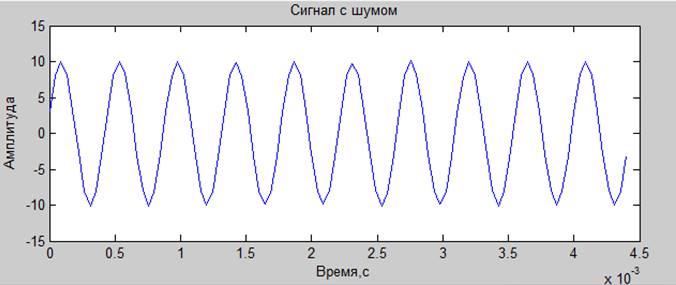
Смесь гармонического сигнала и шума (гауссового)

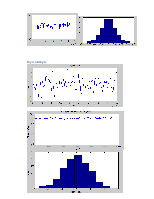
.-40 дб

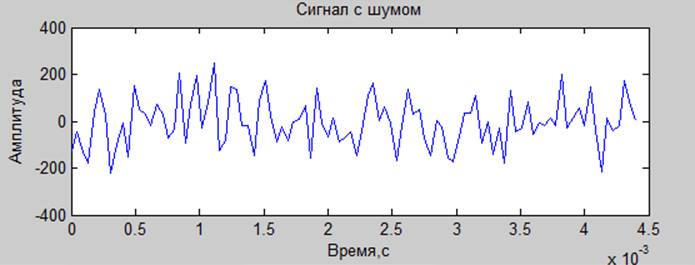
.-20 дб

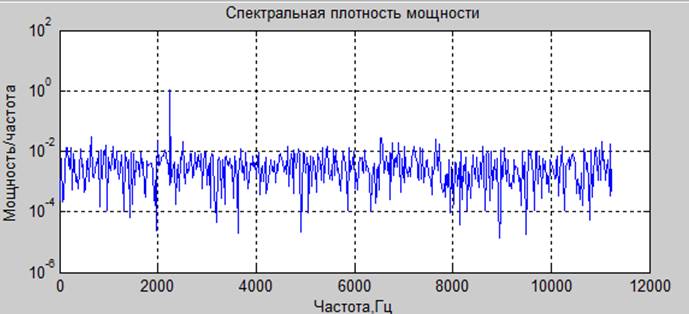
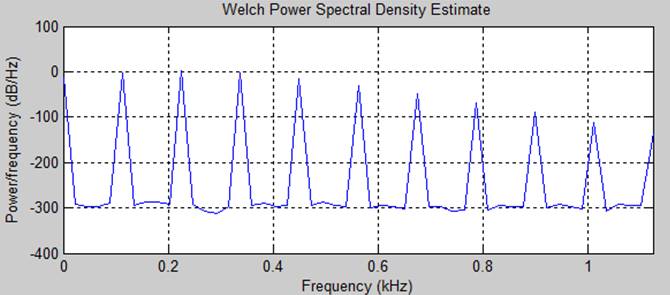
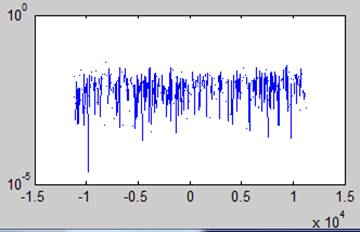
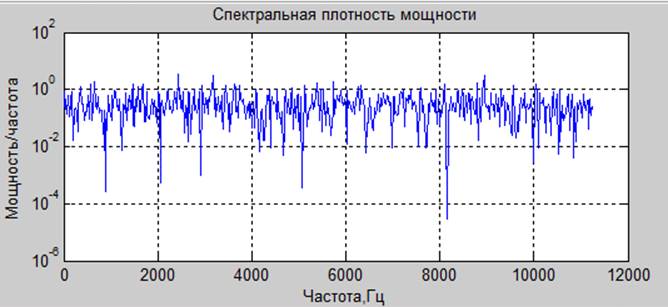
Спектральная плотность с усреднением по частоте

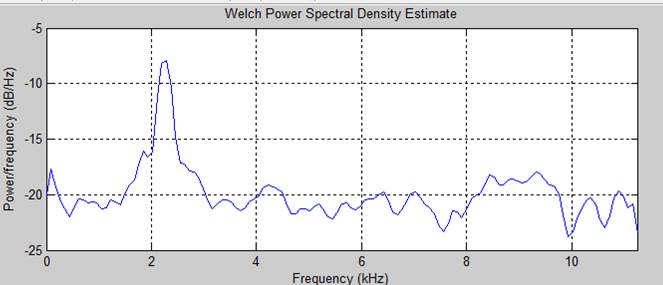
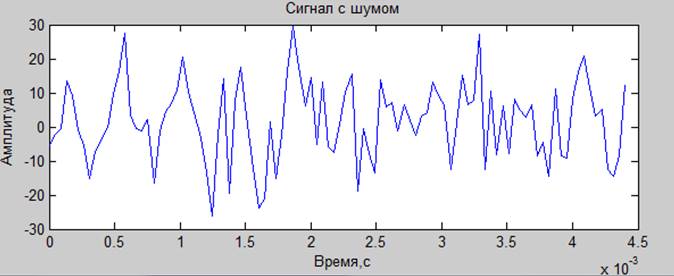
.0 дб

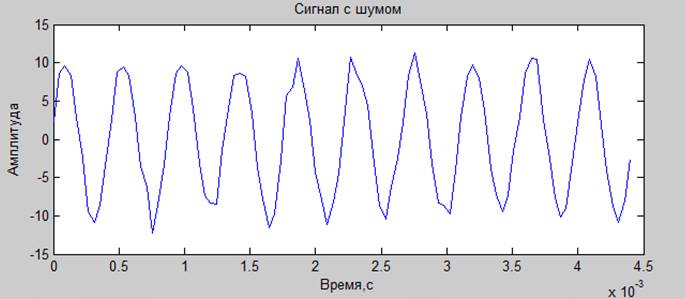
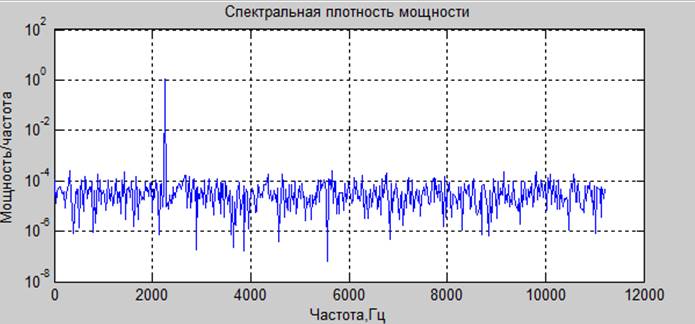
.20 дб

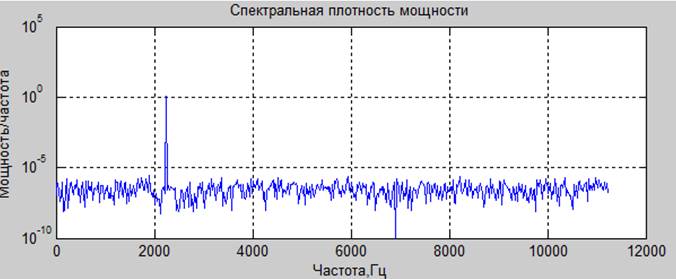
Вывод. При соотношении сигнал/ шум = -20 дб возможно обнаружить гармонический сигнал. Усреднение по частоте помогает ослабить гаусов шум путем загрубления разрешения по частоте в спектре.

Файл lab4.m

clc;

%  Commom lab paramaters

fs = 2250;       % частота несущего сигнала (гармоническая составляющая);

fi = 1125;       %  частота информационного сигнала

fd = 22500;      % частота дискретизации   = 1/ ?t; (из варианта )

N = 1000 -1;        % число отсчетов сигнала;    (кратно периоду)

dt = 1/fd;       % – интервал дискретизации

tBeg = 0;

tEnd = N * dt;   % – длина реализации   = N * ?t, (интервал наблюдения);

df = fd/N;       % разрешение по частоте   = Fd / N;

fd/2;            % - полоса анализа сигнала

f0 = 0.3;        %  начальная фаза

modulationDeep = 0.4;   % глубина модуляции

t = (tBeg : dt : tEnd);  % формирование времени отсчетов

format long

signalAmplitude = 10;   % амплитуда несущего сигнала

informationAmplitude = 9; % амплитуда информационного сигнала

signalNoize = -5;         % в децибеллах

noizeAmplitude = signalAmplitude / 10^(signalNoize/20);

% Гармонический несущий сигнал

harmonySignal = signalAmplitude * sin (2 * pi * fs * t + f0);

% Гармонический информационный сигнал

informationSignal = informationAmplitude * sin (2 * pi * fi * t);

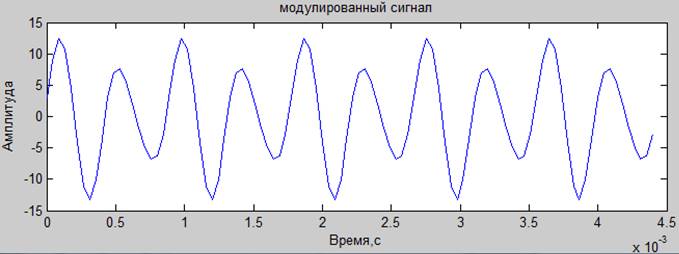
modulatedAmplitudeSignal = harmonySignal .* (1 + modulationDeep * informationSignal); %модулированный амплитудно сигнал

% processSignal(modulatedAmplitudeSignal, fs ,fd, N, dt, tBeg, tEnd, df, t, 'модулированный амплитудно сигнал');

% partialProcess(modulatedAmplitudeSignal, fs ,fd, N, dt, tBeg, tEnd, df, t, 'модулированный амплитудно сигнал');

modulationParam = 1;

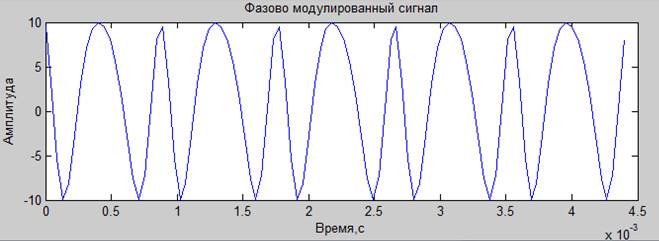
modulatedPhaseSignal = signalAmplitude * cos(2* pi * fs * t + modulationParam * informationSignal + f0); %Фазово модулированный сигнал

% processSignal(modulatedPhaseSignal, fs ,fd, N, dt, tBeg, tEnd, df, t, 'Фазово модулированный сигнал');

% partialProcess(modulatedPhaseSignal, fs ,fd, N, dt, tBeg, tEnd, df, t, 'Фазово модулированный сигнал');

modulationParam = 1;

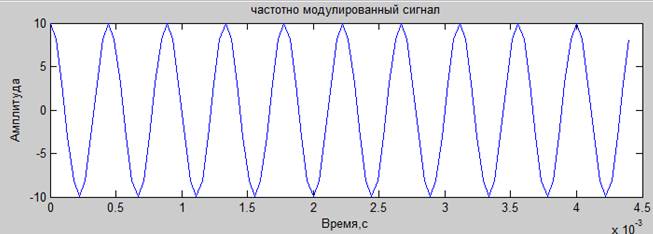
modulatedFrequencySignal = signalAmplitude * fmmod(informationSignal, fs, fd, modulationParam); %частотно модулированный сигнал