









Часть 2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ СИСТЕМ
ОСНОВНЫЕ СИСТЕМНО-ТЕОРЕТИЧЕСКИЕ ЗАДАЧИ
В предыдущем разделе мы рассмотрели некоторые основные способы описания систем и их взаимодействия с человеком и окружающей средой. Вообще говоря, математическое описание позволяет выделить важные свойства рассматриваемой системы и формально определить взаимосвязи между ее различными компонентами. Поскольку использование тех или иных математических абстракций, которыми оперирует теория систем, зависит от поставленной задачи, то мы рассмотрим различные вопросы, такие как глобальные свойства систем, идентификация, оптимизация систем, стохастические процессы, управляемые динамические системы (процессы) и т.д. Их изучение дает важные системно-теоретические результаты и на них в определенной степени, базируется изложение многих основных проблем теории больших систем.
Глобальные свойства системы. В настоящее время существенно увеличилось число проблем, решение которых не может быть получено редукционистскими методами, что, в свою очередь, возродило интерес к изучению и развитию холистских (или глобальных) подходов.
Для иллюстрации фундаментального различия между локальным и глобальным описанием системы рассмотрим простой пример – математический маятник.
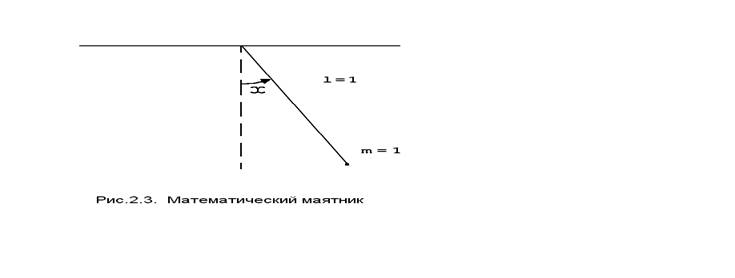
Если отклонение маятника от вертикали обозначим через x(t) , то в локальной окрестности любого такого положения можно записать динамические уравнения движения
d2x/dt2 + sin x = 0, x(0) = x0 , x(0) = 0,
в безразмерных единицах. Это уравнение описывает локальное поведение маятника в (бесконечно малой) окрестности положения x(t). Редукционист попытался бы "склеить" подобные локальные описания для последовательных точек в надежде достичь понимания глобального поведения. Иногда такой подход оказывается успешным, однако, непредвиденные проблемы, возникающие при его использовании, существенно снижают его эффективность.
Холист, приступая к решению этой же задачи, прежде всего заметил бы, что должны соблюдаться определенные глобальные свойства системы, и поэтому любое локальное поведение должно удовлетворять ограничениям, налагаемым глобальными свойствами. Если к тому же эти ограничения достаточно жестки, то можно ожидать, что любые локальные движения ими определяются однозначно.
В случае движения маятника эти глобальные ограничения определяются принципом Гамильтона-Якоби, согласно которому, глобальное движение системы соответствует минимуму полной энергии системы. Вводя гамильтониан
Н = Кинетическая энергия + Потенциальная энергия
видим, что движение системы должно быть таким, что гамильтониан
H(x, dx/dt) = (0,5)×(dx/dt)2 + 1 - cos x
достигает минимума. Это уравнение, очевидно, может быть сведено к уравнению движения маятника, приведенному выше. Другими словами, локальные уравнения движения могут быть получены как следствие глобального принципа, а не выведены на основе рассуждений локального характера и использования второго закона Ньютона. С концептуальной точки зрения такое различие является фундаментальным.
В качестве еще одного примера использования глобального подхода для решения системных задач рассмотрим ситуацию с заторами на транспортной магистрали. Учитывая наличие множества факторов, влияющих на дорожную ситуацию, можно попытаться склеить локальные ситуации, полученные методом Монте-Карло или методами теории очередей и т.д. Такой подход позволяет выявить множество деталей, однако в большинстве случаев остается неясным, как можно использовать полученные результаты для анализа других дорожных ситуаций. Холистский подход в этом случае предполагает использование методов статистической физики. Можно описать подобную ситуацию одним уравнением, пренебрегая дистанцией между машинами, причинами заторов и т.д. Главным для него было бы значение параметра q – плотности потока машин (число машин в час на километр пути). Время TА (минуты), необходимые для преодоления 1 км дороги, можно представить как сумму двух слагаемых
TА = TАО + k×nА ,
где TАО – время, необходимое для преодоления участка дороги длиной А =1 без учета помех со стороны других машин (q = 0, ТАО = 0,5 мин/км соответствует скорости свободного движения 120 км/час);
k×nА – дополнительное время, необходимое для преодоления участка А = 1 км, пропорциональное числу машин nА, находящихся на участке А в течение времени TА (т.е. задержка в условиях заторов является линейной функцией числа торможений и ускорений, или числа nА машин, участвующих в движении). Число nА – является произведением плотности потока машин (транспорта) q и длительности периода времени TА:
nА = q×TА / 60 .
Учитывая предыдущие соотношения, получаем
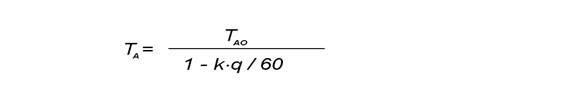
Функция TА = f(q) является выпуклой: каждая дополнительная машина, приводящая к росту плотности потока q , не только задерживается на участке А, но и является причиной задержки других машин. При значениях TА = 0,5 и k = 0,0266 имеется хорошее согласие между
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.