Лекция 7.
СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ СЛУЧАЙНОГО ПРОЦЕССА
Подразумевая под случайным процессом множество (ансамбль) реализаций, необходимо иметь в виду, что реализациям, обладающим различной формой, соответствуют различные спектральные характеристики. Усреднение комплексной спектральной плотности по всем реализациям приводит к нулевому спектру процесса (при среднем = 0) из-за случайности и независимости фаз спектральных составляющих в различных реализациях. Можно, однако, ввести понятие спектральной плотности среднего квадрата случайной величины, поскольку величина среднего квадрата не зависит от соотношения фаз суммируемых гармоник. Если под случайной функцией x(t) подразумевается электрическое напряжение или ток, то средний квадрат этой функции можно рассматривать как среднюю мощность, выделяемую в сопротивлении 1 Ом. Эта мощность распределена по частотам в некоторой полосе, зависящей от механизма образования случайного процесса. Спектральная плотность средней мощности представляет собой среднюю мощность, приходящуюся на 1 Гц при заданной частоте ω. Введенную таким образом спектральную плотность S(ω) в дальнейшем будем называть энергетическим спектром функции x(t). Смысл такого названия определяется размерностью функции S(ω), являющейся отношением мощности к полосе частот:
[S(ω)] = [ мощность/ полоса частот ] = [мощность×время] = [энергия],
Энергетический спектр можно найти, если известен механизм образования случайного процесса. Здесь же мы ограничимся некоторыми определениями общего характера.
Методы вычисления СПМ
Функции спектральной плотности можно определять тремя различными эквивалентными способами, которые мы рассмотрим ниже:
- с помощью ковариационных функций;
- с помощью финитного преобразования Фурье;
- с помощью фильтрации, возведения в квадрат и усреднения.
Определение спектров с помощью корреляционных функций.
Исторически первый способ определения
спектральной плотности появился в математике. Он состоит во взятии
преобразования Фурье от предварительно вычисленной корреляционной функции.
После вычитания средних значений такие (бесконечные) преобразования Фурье
обычно существуют, даже если (бесконечное) преобразование Фурье исходного
процесса не существует. Этот подход дает
двустороннюю спектральную плотность, определенную для частот f от -![]() до
+
до
+![]() и обозначаемую S(f).
и обозначаемую S(f).
Пусть существуют корреляционные и взаимная корреляционная функции Rx(t),Ry(t) и Rxy(t). Предположим также, что конечны интегралы от их абсолютных величин
![]() R(
R(![]() d
d![]()
На практике эти условия всегда выполняются для реализаций конечной длины. Тогда ПФ функций R(t) существуют и определяются формулами
Sx(f)=![]()
![]()
Sy(f)=![]()
![]() (1)
(1)
Sxy(f)=![]()
![]()
Такие
интегралы по конечным реализациям существуют всегда. Функции Sx(f) и Sy(f) называют функциями
спектральной плотности процессов x(t) и y(t)
соответственно или просто спектральными плотностями, а функцию ![]() называют взаимной спектральной плотностью двух процессов
x(t) и y(t) .
называют взаимной спектральной плотностью двух процессов
x(t) и y(t) .
Обратные ПФ от формул (1) дают
Rx(τ) =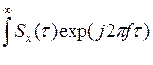
![]()
Ry(τ) =![]()
![]() (2)
(2)
Rxy(τ)
=![]() df.
df.
Соотношения (1) и (2) называют формулами Винера-Хинчина, которые в 30-е годы независимо установили связь между корреляционными функциями и спектральной плотностью через ПФ. При решении практических задач приходится допускать в R(t) и S(f) наличие дельта-функций.
Из свойств симметрии стационарных ковариационных функций следует
Sx(-f) = Sx(f) a Sxy(-f) = Syx(f)
Следовательно, спектральная плотность Sx(f) – действительная четная функция, a Sxy(f) – комплексная функция от f.
Тогда спектральные соотношения из (1) можно преобразовать к виду
Sx(f)=
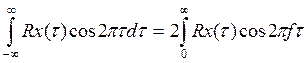 d
d![]() (3)
(3)
Односторонние спектральные плотности Gx(f), где f
изменяется только в пределах интервала (0,![]() ),
определяются формулами
),
определяются формулами
|
||||
Gx(f)=
Рисунок 1 иллюстрирует связь между этими функциями.
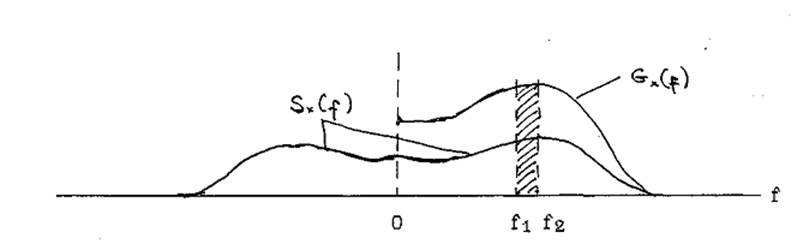
Рис.1. Односторонняя и двусторонняя спектральные плотности.
Именно эти величины измеряются на практике с помощью прямой фильтрации
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.