Исследование детерминированных процессов. Гармонические, периодические, квазипериодические и непериодические процессы

Отчет по лабораторной работе № 1

Исследование детерминированных процессов

Вариант 6

Выполнил

5 курс 1 группа

Цель работы: изучить гармонические, периодические, квазипериодические и непериодические процессы. При исследовании необходимо решить следующее задачи:

- синтезировать процессы во временной области;

- вычислить корреляционные характеристики;

- вычислить спектральные характеристики.

Частота основного тона гармонических и периодических процессов должна быть кратна и не кратна разрешению по частоте (длительность реализации кратна и не кратна периоду основного тона). В качестве периодических рассмотреть «меандр», «равнобокую» и «кособокую» пилу –    |_|ˉˉ|_|ˉˉ|_|ˉˉ|_|ˉˉ|_     /|/|/|/|/|/|     |\|\|\|\|\|\     /\/\/\/\/\/\/.

Важные параметры в моделировании процессов следующие:

f_s = 95;             % частота сигнала (гармоническая составляющая);

F_d =360;           % частота дискретизации   = 1/ Δt;

N=50;               %число отсчетов сигнала;

T = N * Δt =0,2;         %длина реализации   (интервал наблюдения);

Δt = 1/F_d = 0,004;       %интервал дискретизации;

Δf = F_d / N = 5;          %разрешение по частоте;

F_d /2 =1100;               %полоса анализа сигнала.

1.  Синтезированные процессы (F_d=2200, f_s=600). Для наглядности приведены только первые 0.2 с процесса.

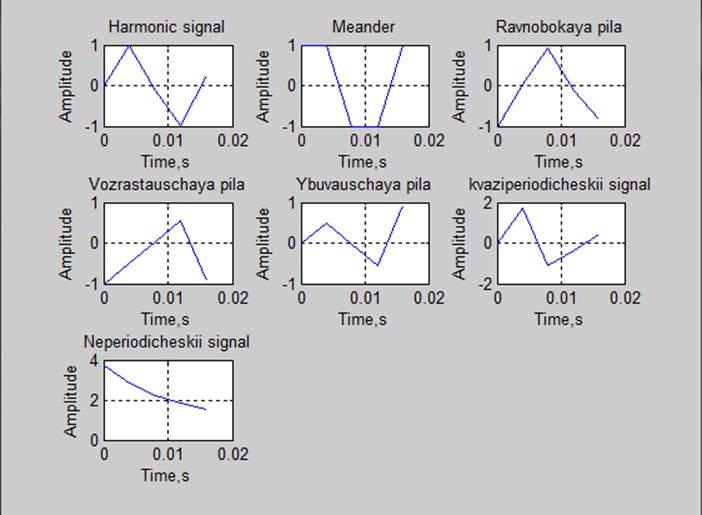
Ввиду малого отношения частоты дискретизации к частоте сигналов, они оказались искажены.

2. Мощностипроцессов

                                      |multiple to T |aliquant to T

Harmonic signal               |    0.50000|    0.50000

Meander                            |    1.01999|    1.01332

Ravnobokaya pila            |    0.35439|    0.34773

Vozrastauschaya pila       |    0.35357|    0.34026

Ybuvauschaya pila           |    0.31360|    0.31360

kvaziperiodicheskii signal|    0.96318|    1.00695

Neperiodicheskii signal    |    1.59118|    1.39573

Вывод: полученные оценки мощности для различных длительностей реализаций практически совпадают.

3. Корреляционные характеристики

 

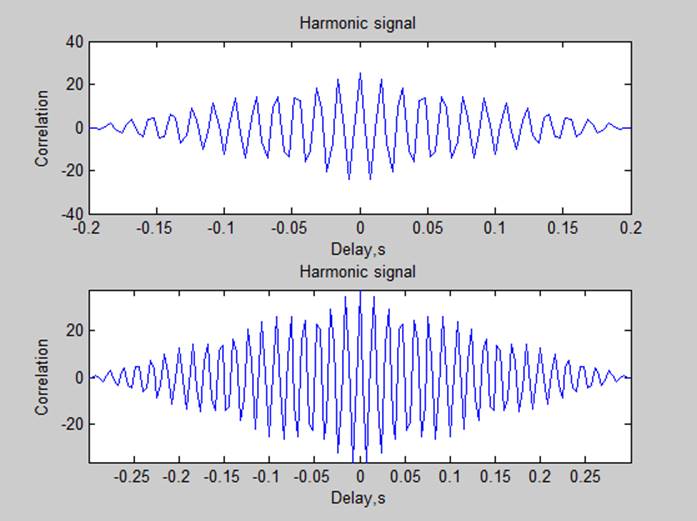
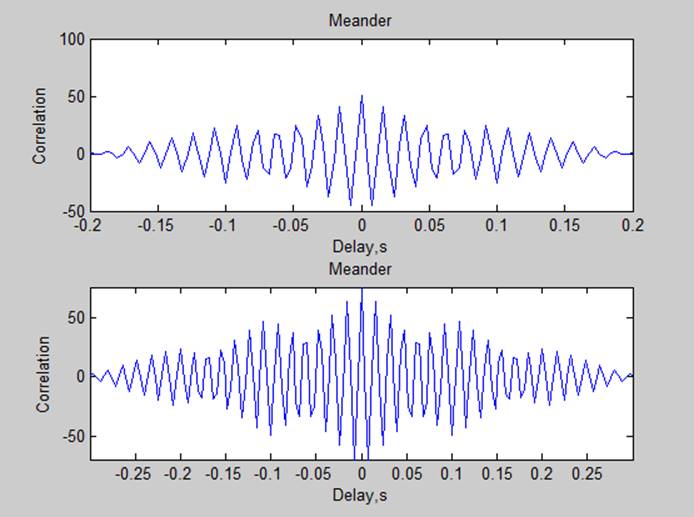
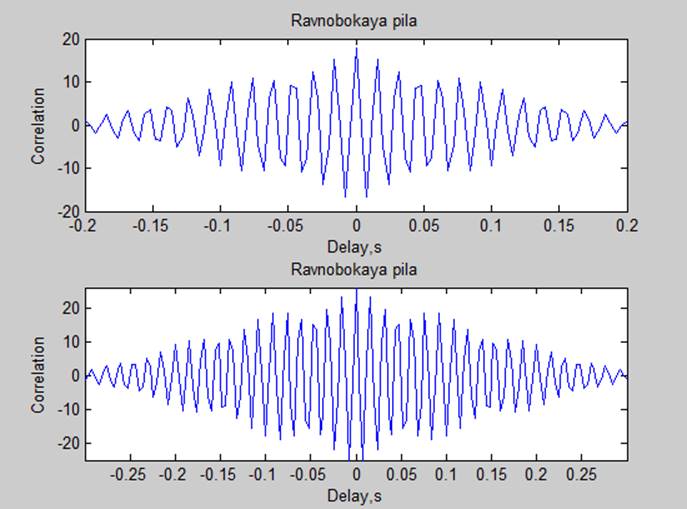
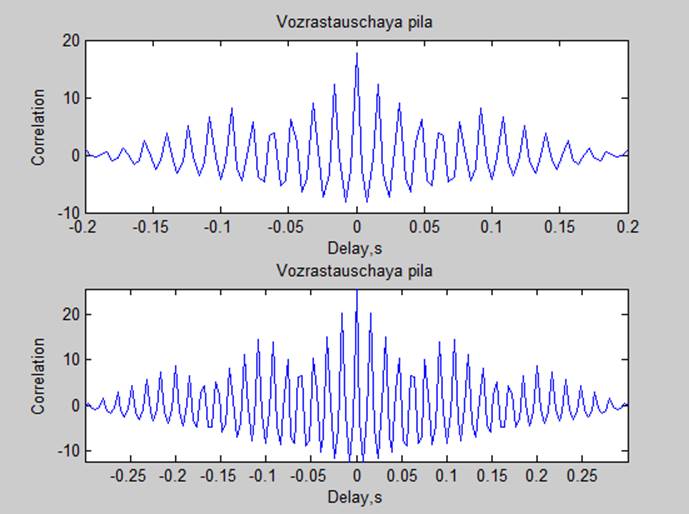
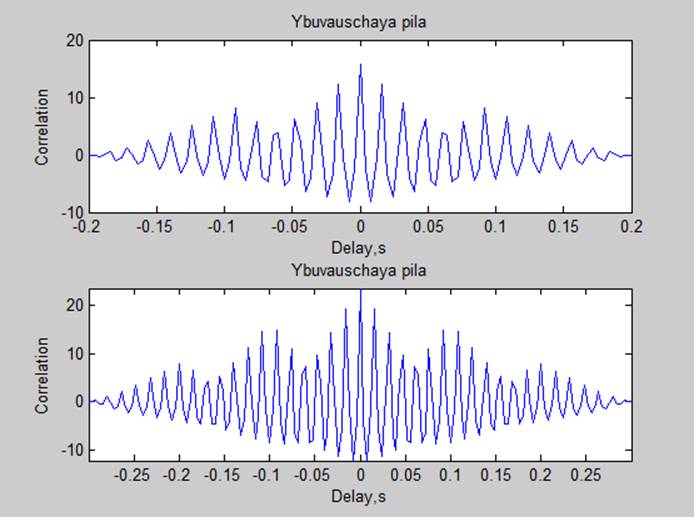
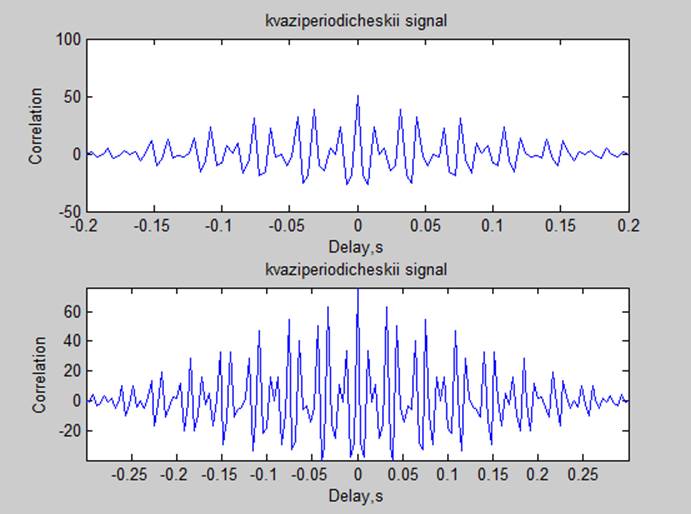
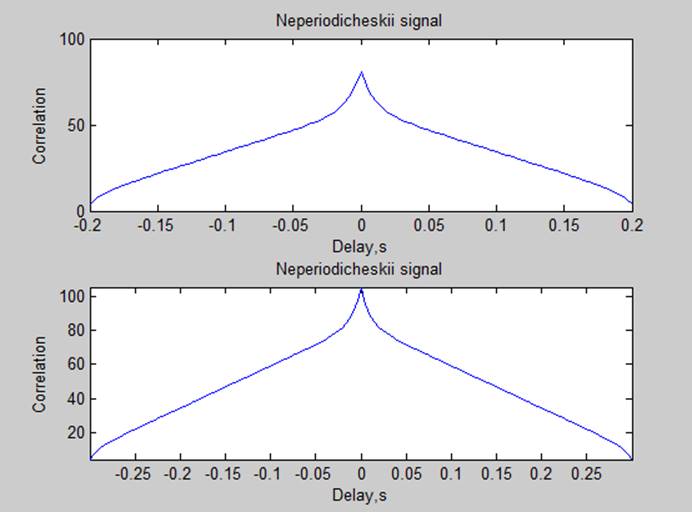
Мощности сигналов по автокорреляционной характеристике (P=R(0)/N):

                                        multiple to T|    aliquant to T

          Harmonic signal|           0.50000|    0.50000

                  Meander|                1.02000|    1.01333

         Ravnobokaya pila|          0.35440|    0.34773

     Vozrastauschaya pila|        0.35360|    0.34027

        Ybuvauschaya pila|         0.31360|    0.31360

kvaziperiodicheskii signal|      1.02149|    1.01410

  Neperiodicheskiisignal|    1.61817|    1.41212

Вывод: Оценки мощности по автокорреляционной функции почти совпадают с оценками, полученными ранее.

4. Спектральные характеристики.

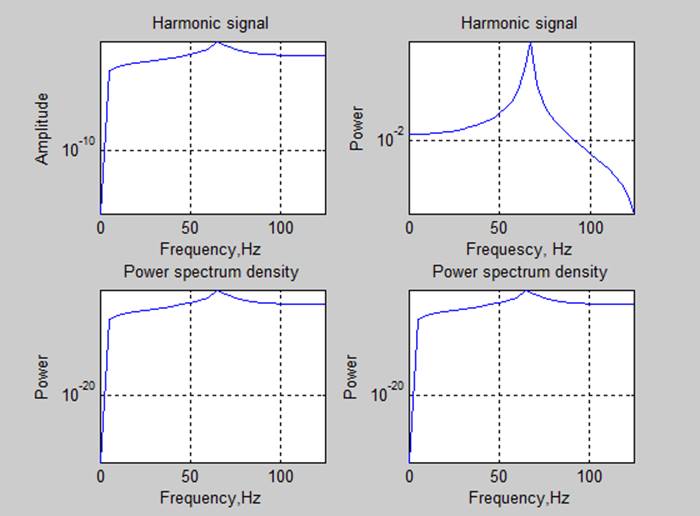
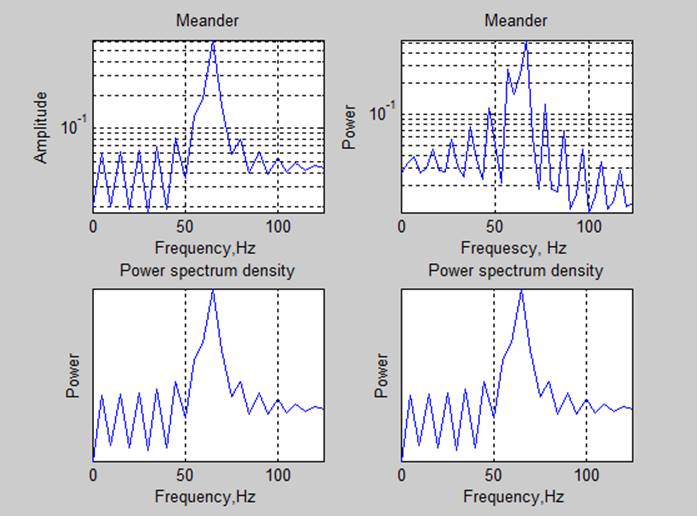
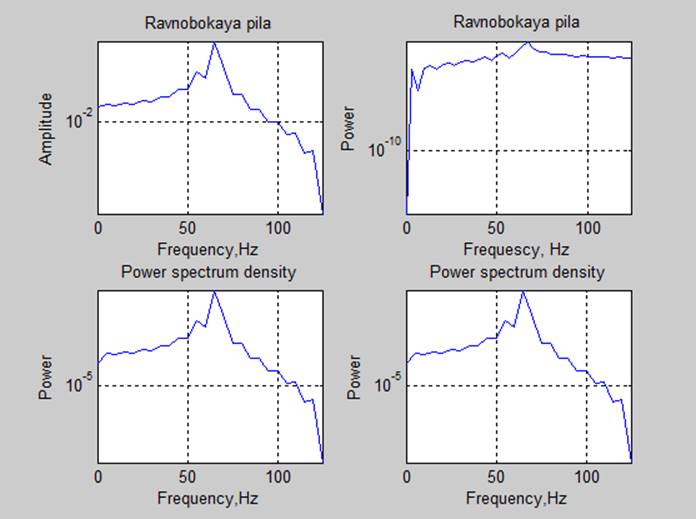
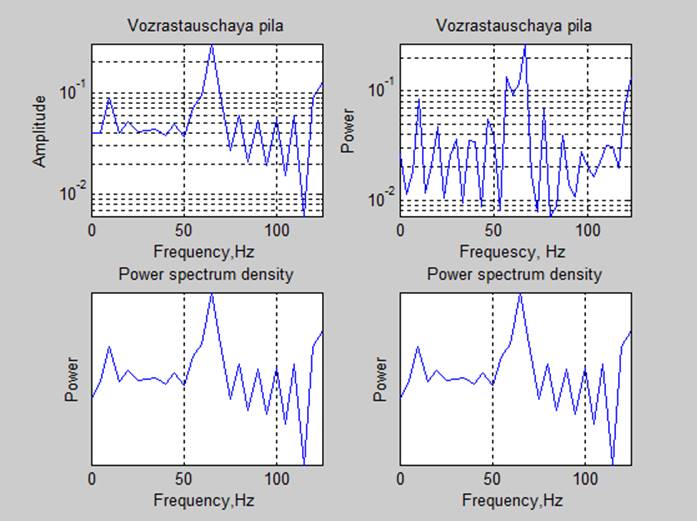
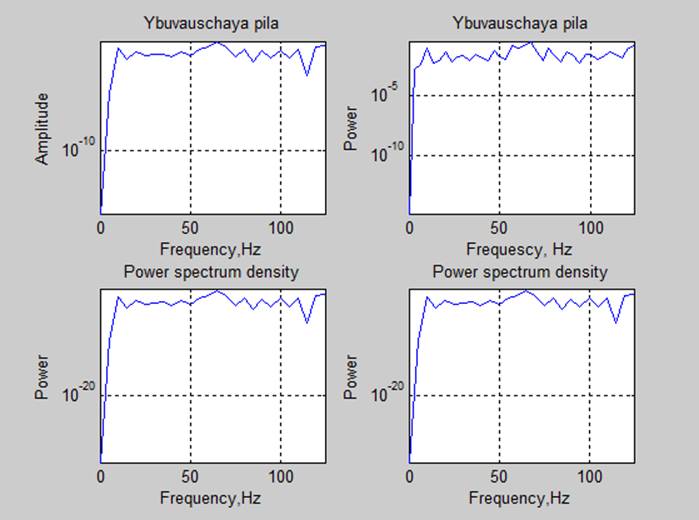
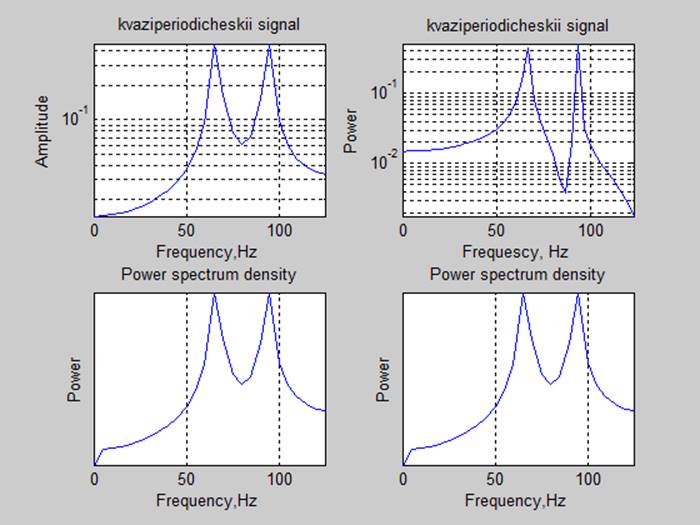
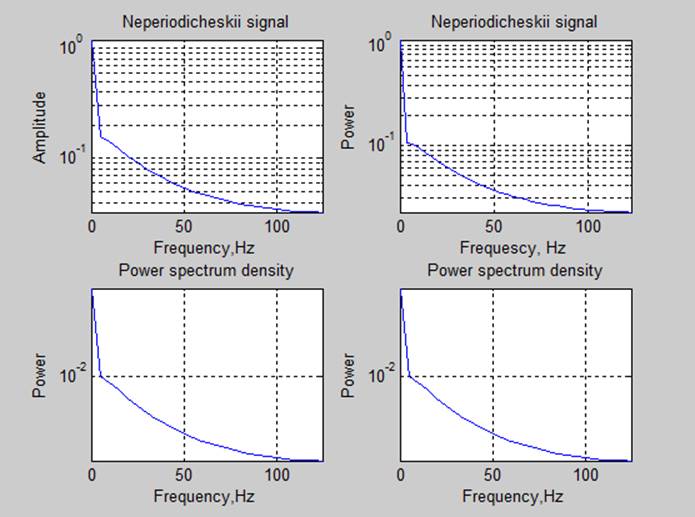
Оценка мощности сигналов с помощью частотных характеристик (P=sum(S(f))*df):

|кр.периоду|  некр.периоду

Harmonic signal|        0.51000|    0.50667

Meander|            1.04040|    1.02613

Ravnobokaya pila|      0.36149|    0.35215

Vozrastauschaya pila|     0.36067|    0.33410

Ybuvauschaya pila|      0.31987|    0.31188

kvaziperiodicheskii signal|   1.04192|    1.02762

Neperiodicheskii signal|     1.65054|    1.43047

Вывод: Спектр сигналов, длительность реализации которого была кратна периоду основного тона, имеет более выраженные пики. Так же оценки мощности сигнала, полученные с помощью спектральной плотности мощности соответствуют с точностью до 3 знака полученным ранее оценкам.

Листинг программы

clc;

clear;

%характеристики сигнала

fs=65; %частота сигнала(гармоническая состовляющая)

Fd=250; %частота дискретизации

fsm=fs*sqrt(2); %доп.частота для квазипериодического сигнала

Tm=0.2; %время выборки кратное периоду сигнала

nm=Fd*Tm;

Tn=0.3; %время выборки не кратное периоду сигнала

nn=Fd*(0.3);

timem=0:1/Fd:Tm; %вектор времени (кратный периоду)

timen=0:1/Fd:0.3; %вектор времени (не кратный периоду)

% Создадим сигналы

fprintf('Power of Signals:\n');

fprintf('                          |multiple to T|aliquant to T\n');

%Гармонический сигнал

msignals(1,:)=sin(2*pi*fs*timem); %гармонический сигнал частотой 600гц

nsignals(1,:)=sin(2*pi*fs*timen); %гармонический сигнал частотой 550гц

names{1}='Harmonic signal';

mmean=mean(sin(2*pi*fs*timem)); %мат.ожидание сигнала с частатой 600гц

nmean=mean(sin(2*pi*fs*timen)); %мат.ожидание сигнала с частатой 550гц

mcov=cov(sin(2*pi*fs*timem)); %дисперсия сигнала с частатой 600гц

ncov=cov(sin(2*pi*fs*timen)); %дисперсия сигнала с частатой 550гц

mpower=mmean.^2+mcov; %мощность сигнала с частатой 600гц

npower=nmean.^2+ncov; %мощность сигнала с частатой 550гц

fprintf('%25s|%11.5f|%11.5f\n',names{1},mpower,npower);

%Периодические сигналы

%Меандр

msignals(2,:)=square(2*pi*fs*timem); %меандр с частотой 600гц

nsignals(2,:)=square(2*pi*fs*timen); %меандр с частото1 550гц

names{2}='Meander';

mmean=mean(square(2*pi*fs*timem)); %мат.ожидание сигнала с частатой 600гц

nmean=mean(square(2*pi*fs*timen)); %мат.ожидание сигнала с частатой 550гц

mcov=cov(square(2*pi*fs*timem)); %дисперсия сигнала с частатой 600гц

ncov=cov(square(2*pi*fs*timen)); %дисперсия сигнала с частатой 550гц

mpower=mmean.^2+mcov; %мощность сигнала с частатой 600гц

npower=nmean.^2+ncov; %мощность сигнала с частатой 550гц

fprintf('%25s|%11.5f|%11.5f\n',names{2},mpower,npower);

%Равнобокая пила

msignals(3,:)=sawtooth(2*pi*fs*timem,0.5); %равнобокая пила с частотой 600гц

nsignals(3,:)=sawtooth(2*pi*fs*timen,0.5); %равнобокая пила с частотой 550гц