Лабораторная работа № 4
Измерение спектральных характеристик стохастических процессов в реальном масштабе времени
Вариант 9
Выполнила
4 курс 1 группа
Цель работы. Провести исследование аддитивной модели смеси сигнала и «белого» гауссова шума с различным отношением сигнал/шум. Выделить сигнал из шума для различных значений разрешающей способности анализа.
1. Сгенерированные сигналы:
Была сгенерирована смесь гармонического сигнала амплитуды 1 и Гауссова шума с различной дисперсией, соотношения сигнал/шум брались -40, -20, 0, 20 дБ.
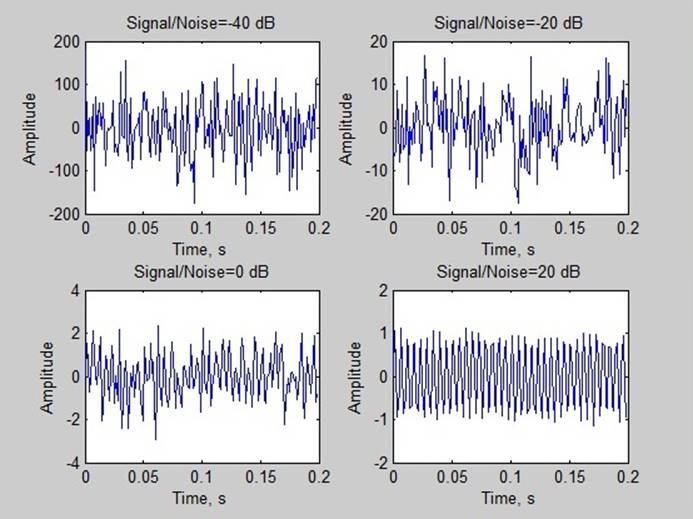
2. Спектры сигналов
Рассматривались последовательности 10 секунд (3600 отсчетов, разрешение 0.1 Гц) и 1 секунда (360 отсчетов, разрешение 1 Гц). При усреднении брались 6 отрезков сигналов.
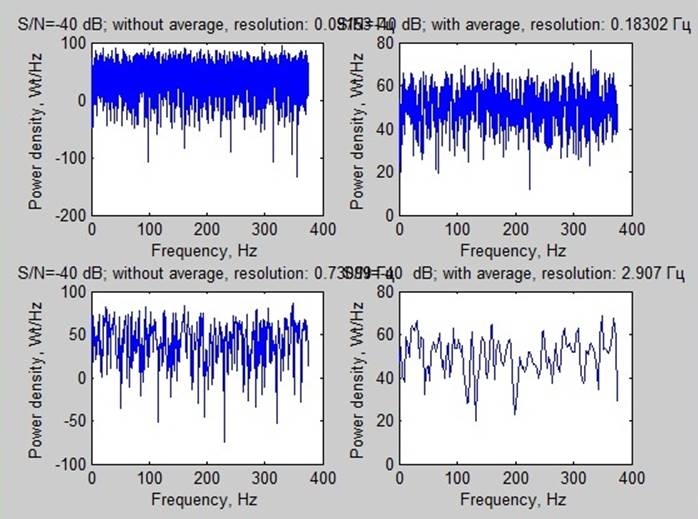
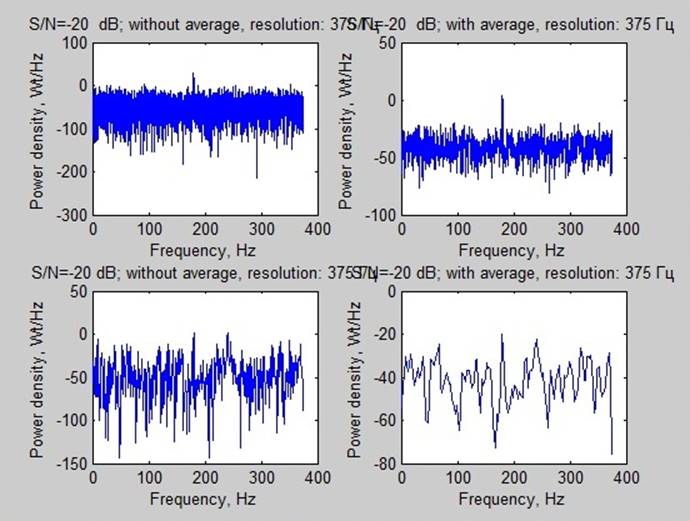
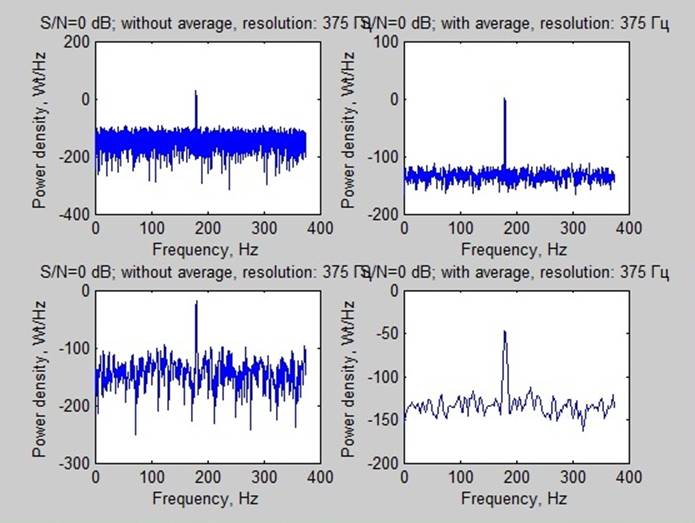
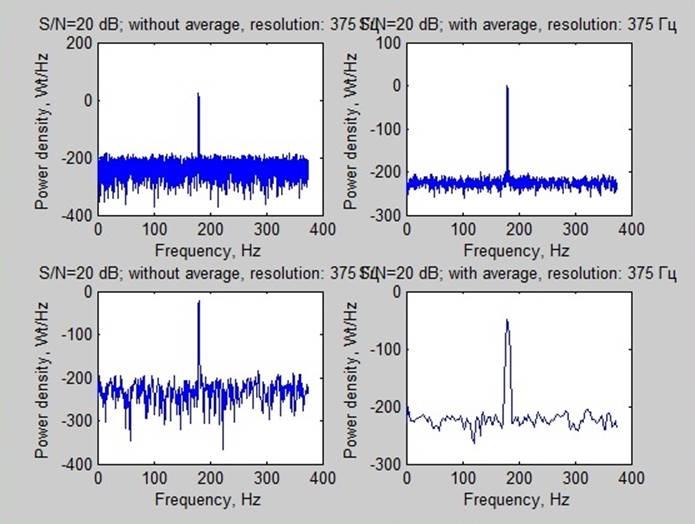
Вывод: Наиболее показательными являются спектры мощности при соотношении сигнал/шум -20 дБ. На них можно заметить, что усреднение, приводящее к уменьшению разрешения, улучшает возможности обнаружения сигнала. Вместе с тем чем больше данных возможно собрать (больше время наблюдения и больше разрешения) тем успешнее возможно выделить сигнал.
Листинг программы
clear all;
Fd=750;
fs=180;
T=10; % время сигнала, большое разрешение
t=1; % время сигнала, малое разрешение
naverage=6;
N=T*Fd; % количество отсчетов
n=t*Fd;
Time=(0:N-1)/Fd;
time=(0:n-1)/Fd;
%% Генерируем сигнал с разными соотношениями шума
a0=1; % амплитуда сигнала
Signal=a0*sin(2*pi*fs*Time);
signal=a0*sin(2*pi*fs*time);
S2N=[-40 -20 0 20]; % соотношения сигнал-шум
sigma=sqrt(a0^2./2./(10.^(S2N/10)));
for i=1:4
Data(i,:)=Signal+sigma(i)*randn(1,N);
data(i,:)=signal+sigma(i)*randn(1,n);
end
%% Нарисуем сигналы
figure;
dt=0.2;
dn=dt*Fd;
for i=1:4
subplot(2,2,i);
plot(time(1:dn),data(i,1:dn));
title(['Signal/Noise=' num2str(S2N(i)) ' dB']);
xlabel('Time, s');
ylabel('Amplitude');
end
%% Для каждого сигнала посчитаем спектр мощности с/без усреднением и
% различным разрешением.
% без усреднения большое разрешение
win=ones(1,N);
[Power1, Freq1]=pwelch(Data(1,:),N,[],[],Fd);
PowersWO1=Power1;
FreqsWO1=Freq1;
[Power2, Freq2]=pwelch(Data(2,:),N,[],[],Fd);
PowersWO2=Power2;
FreqsWO2=Freq2;
[Power3, Freq3]=pwelch(Data(3,:),N,[],[],Fd);
PowersWO3=Power3;
FreqsWO3=Freq3;
[Power4, Freq4]=pwelch(Data(4,:),N,[],[],Fd);
PowersWO4=Power4;
FreqsWO4=Freq4;
% без усреднения малое разрешение
win=ones(1,n);
[power1 freq1]=pwelch(data(1,:),n,[],[],Fd);
powersWO1=power1;
freqsWO1=freq1;
win=ones(1,n);
[power2 freq2]=pwelch(data(2,:),n,[],[],Fd);
powersWO2=power2;
freqsWO2=freq2;
win=ones(1,n);
[power3 freq3]=pwelch(data(3,:),n,[],[],Fd);
powersWO3=power3;
freqsWO3=freq3;
win=ones(1,n);
[power4 freq4]=pwelch(data(4,:),n,[],[],Fd);
powersWO4=power4;
freqsWO4=freq4;
% с усреднением большое разрешение
win=ones(1,floor(N/naverage));
[Power1 Freq1]=pwelch(Data(1,:),floor(2*N/(naverage+1)),[],[],Fd);
PowersW1=Power1;
FreqsW1=Freq1;
win=ones(1,floor(N/naverage));
[Power2 Freq2]=pwelch(Data(2,:),floor(2*N/(naverage+1)),[],[],Fd);
PowersW2=Power2;
FreqsW2=Freq2;
win=ones(1,floor(N/naverage));
[Power3 Freq3]=pwelch(Data(3,:),floor(2*N/(naverage+1)),[],[],Fd);
PowersW3=Power3;
FreqsW3=Freq3;
win=ones(1,floor(N/naverage));
[Power4 Freq4]=pwelch(Data(4,:),floor(2*N/(naverage+1)),[],[],Fd);
PowersW4=Power4;
FreqsW4=Freq4;
% с усреднением малое разрешение
win=ones(1,floor(n/naverage));
[power1 freq1]=pwelch(data(1,:),floor(2*n/(naverage+1)),[],[],Fd);
powersW1=power1 ;
freqsW1=freq1;
win=ones(1,floor(n/naverage));
[power2 freq2]=pwelch(data(2,:),floor(2*n/(naverage+1)),[],[],Fd);
powersW2=power2 ;
freqsW2=freq2;
win=ones(1,floor(n/naverage));
[power3 freq3]=pwelch(data(3,:),floor(2*n/(naverage+1)),[],[],Fd);
powersW3=power3 ;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.