Лабораторная работа № 3
Изучение измерительных информационных систем для анализа стохастических процессов (на примере анализатора СК4-72)
5 курс 8 группа
8 вариант
Задачи:
1. Смоделировать процедуру вычисления спектральных характеристик методом фильтрации с использованием гетеродина;
2. Изучить функциональную схему и органы управления анализатора с временной компрессией СК4-72.
3. Смоделировать процедуру вычисления спектральных характеристик методом фильтрации с использованием гетеродина;
Ход выполнения:
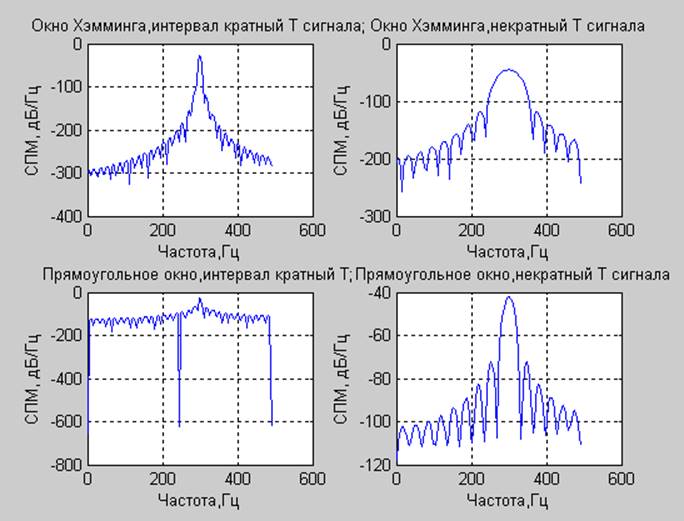
1. Использование различных окон для оценки амплитуды гармонической составляющей
Спектр плотности мощности гармонического сигнала (fs= 300, Fd= 980) оценивался методом периодограмм с использованием окна Хэмминга и прямоугольного окна различных длин.
2. Моделирование методов оценки спектра
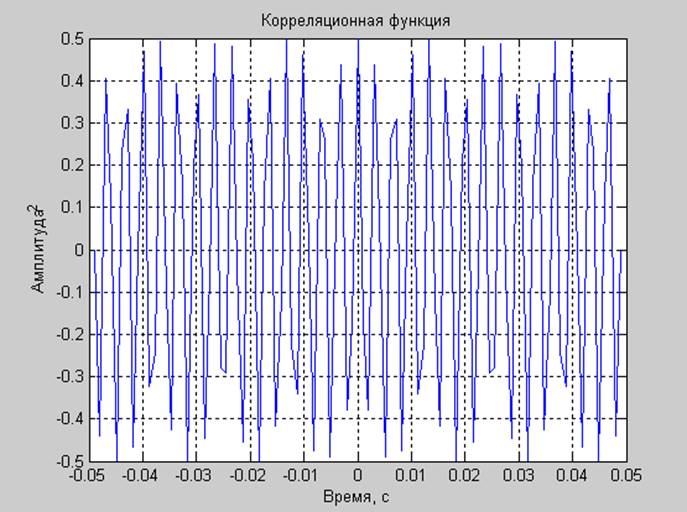
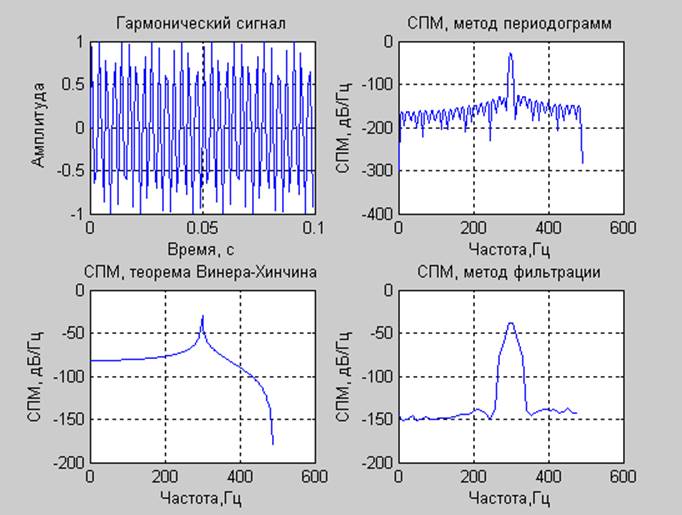
Стационарный сигнал
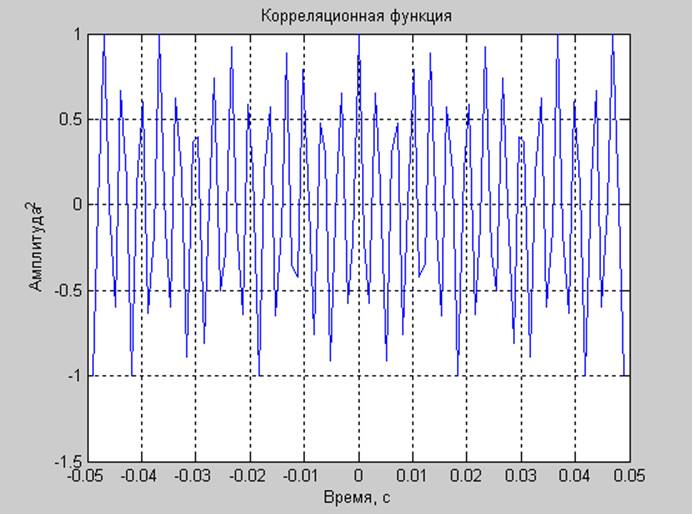
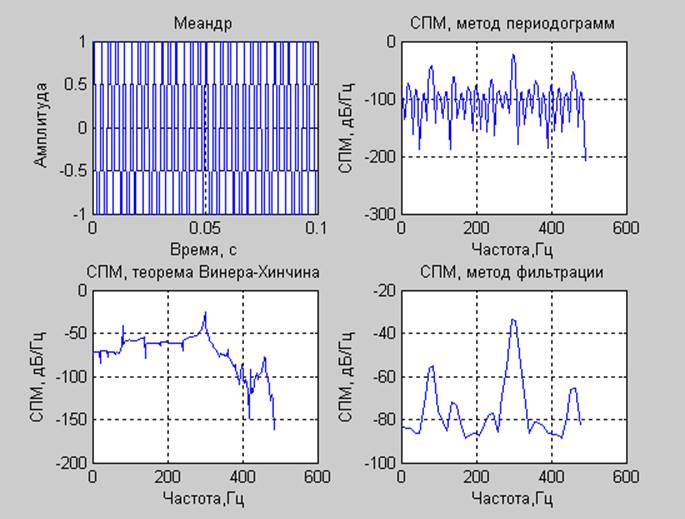
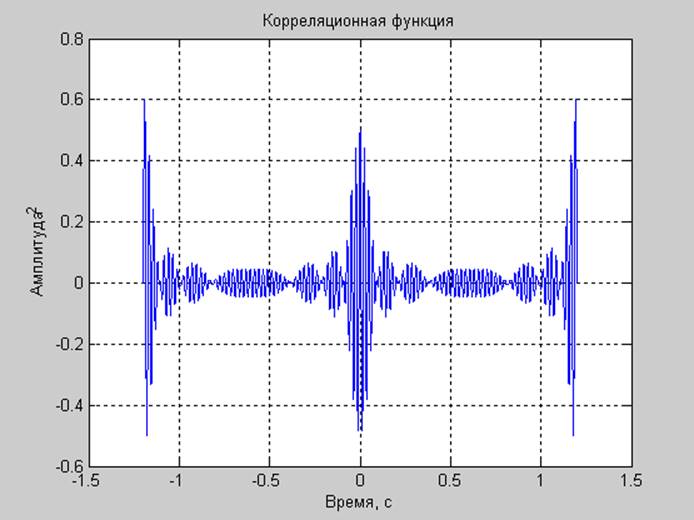
Меандр
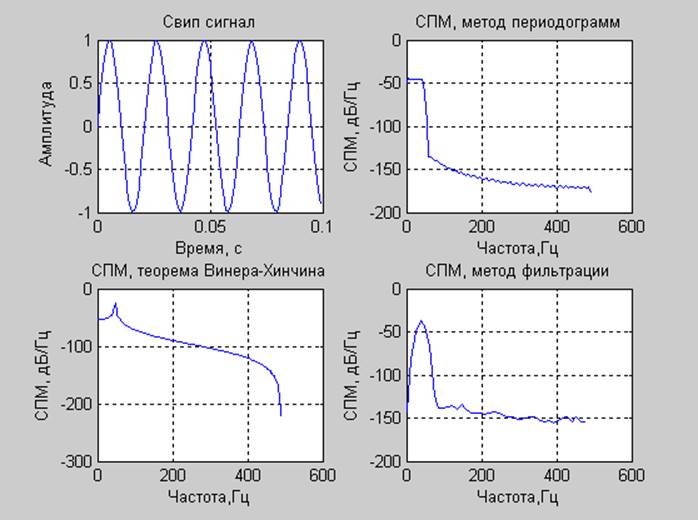
Свип сигнал
Проверка мощностей:
|
Сигнал |
Суммарная мощность процесса |
мощность из оценки методом периодограмм |
мощность из оценки по теореме Винера-Хинчина |
мощность из оценки методом фильтрации |
|
Гармонический сигнал |
0.500051 |
0.496124 |
0.498312 |
0.590090 |
|
Меандр |
1.000102 |
0.992248 |
1.249604 |
1.197128 |
|
Свип сигнал |
0.508985 |
0.504597 |
0.860099 |
0.571562 |
Выводы: Наиболее узкие пики дает метод, основанный на теореме Винера-Хинчина, хотя из-за сложности в получении точной спектральной оценки, он дает ошибку в суммарной мощности. Наиболее точные данные по суммарной мощности дает метод периодограмм.
Полученные графики отчетливо показывают, что анализировать нестационарные сигналы данными методами неэффективно: необходимо либо рассматривать спектр мощности очень коротких кусков сигнала (что негативно отразится на разрешающей способности) либо использовать вейвлет преобразования.
Для реализации метода фильтрации в реальном времени можно уменьшать порог обнаруживаемых сигналов. Для этого нужно прореживать сигнал по частоте. Второй вариант реализации метода фильтрации в реальном времени - использовать одновременно несколько каналов. Количество каналов выбирается по числу частотных областей.
Код программы:
clc;
clear;
Fd=980;
fs=300;
% другие постоянные
T=10;% время длинного процесса
N=T*Fd;%количество отсчетов
time=(0:N-1)/Fd; % вектор моментов времени осчетов
twinmach=0.2; % длительность окна, дающее разрешение попадающее на fs
nwinmach=twinmach*Fd; % количество отсчетов для этого окна
twinpass=300/9800; % длительность окна, когда fs попадет между отсчетами
nwinpass=twinpass*Fd; % количество отсчетов для этого окна
% создадим сигналы
nsignals=3; % количество сигналов
allsignals=zeros(nsignals,N);
% гармонический сигнал
allsignals(1,:)=sin(2*pi*fs*time);
names{1}='Гармонический сигнал';
%периодический - меандр
allsignals(2,:)=square(2*pi*fs*time);
names{2}='Меандр';
%непериодический - свип
K=-fs/T*2;% за время Т частота пройдет через 0 и опять востановится
allsignals(3,:)=sin(fs*time+K/2*(time.^2));
names{3}='Свип сигнал';
%найдем мощности сигналов
means(1)=mean(sin(2*pi*fs*time));
means(2)=mean(square(2*pi*fs*time));
means(3)=mean(sin(fs*time+K/2*(time.^2)));
vars(1)=cov(sin(2*pi*fs*time));
powers(1)=means(1).^2+vars(1);
vars(2)=cov(square(2*pi*fs*time));
powers(2)=means(2).^2+vars(2);
vars(3)=cov(sin(fs*time+K/2*(time.^2)));
powers(3)=means(3).^2+vars(3);
% оценка гармонического сигнала с разными окнами
windows{1}=hanning(nwinmach);
winnames{1}='Окно Хэмминга,интервал кратный T сигнала;';
windows{2}=hanning(nwinpass);
winnames{2}='Окно Хэмминга,некратный T сигнала';
windows{3}=rectwin(nwinmach);
winnames{3}='Прямоугольное окно,интервал кратный T;';
windows{4}=rectwin(nwinpass);
winnames{4}=' Прямоугольное окно,некратный T сигнала';
for i=1:4
subplot(2,2,i);
[pow freq]=pwelch(allsignals(1,:),windows{i},[],[],Fd);
plot(freq,10*log(pow));
title(winnames{i})
xlabel('Частота,Гц');
ylabel('СПМ, дБ/Гц');
grid on;
end;
figure;
[corr lags]=xcorr(allsignals(1,1:nwinmach/4),'unbiased');
plot(lags/Fd,corr);
title('Корреляционная функция');
xlabel('Время, с');
ylabel(' Амплитуда^2');
grid on;
figure;
[corr lags]=xcorr(allsignals(2,1:nwinmach/4),'unbiased');
plot(lags/Fd,corr);
title('Корреляционная функция');
xlabel('Время, с');
ylabel(' Амплитуда^2');
grid on;
figure;
[corr lags]=xcorr(allsignals(3,1:nwinmach*6),'unbiased');
plot(lags/Fd,corr);
title('Корреляционная функция');
xlabel('Время, с');
ylabel(' Амплитуда^2');
grid on;
% оценка различных методов получения спектральных характеристик
for i=1:nsignals
figure;
subplot(2,2,1);
plot(time(1:nwinmach/2),allsignals(i,1:nwinmach/2));
title(names{i});
xlabel('Время, с');
ylabel(' Амплитуда');
grid on;
% Оценка методом периодограмм
[powspec freq]=pwelch(allsignals(i,:),nwinmach,[],[],Fd);
subplot(2,2,2)
plot(freq,10*log(powspec));
title('СПМ, метод периодограмм');
xlabel('Частота,Гц');
ylabel('СПМ, дБ/Гц');
grid on;
% Оценка по теореме Винера-Хинчина
[corr lags]=xcorr(allsignals(i,1:nwinmach),'unbiased');
powercor=fft(corr)/(2*nwinmach-1)/Fd*length(corr);
subplot(2,2,3);
plot(0:1/2/twinmach:Fd/2-1,10*log(abs(real(powercor(1:nwinmach)))));
title('СПМ, теорема Винера-Хинчина');
xlabel('Частота,Гц');
ylabel('СПМ, дБ/Гц');
grid on;
% оценка методом фильтрации
nchunks=40;
chunksize=N/nchunks;
freqband=Fd/2/nchunks;
powerfilt=zeros(1,nchunks);
for j=1:nchunks
chunk=allsignals(i,(1:chunksize)+(j-1)*chunksize);
heterodin=cos(2*pi*(j-1)*freqband*time(1:chunksize));
signal=chunk.*heterodin;
power=pwelch(signal,[],[],[],Fd);
freqbandsize=floor(length(power)/nchunks);
powerfilt(j)=sum(power(1:freqbandsize));
end;
subplot(2,2,4);
plot(0:freqband:Fd/2-freqband,10*log(powerfilt));
title('СПМ, метод фильтрации');
xlabel('Частота,Гц');
ylabel('СПМ, дБ/Гц');
grid on;
fprintf('%s: Суммарная мощность процесса ( sig2 + m2): %f; мощность из оценки методом периодограмм: %f; \n',names{i},powers(i),sum(powspec)*Fd/2/length(powspec));
fprintf('мощность из оценки по теореме Винера-Хинчина %f; методом фильтрации: %f\n',sum(abs(real(powercor(1:nwinmach))))*Fd/2/nwinmach,sum(powerfilt)*freqband);
end;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.