Уводзіны. Элементы тэорыі мностваў і матэматычнай логікі. Рэчаісныя лікі, страница 6

def: Будзем гаварыць, што мнагасклад  дзеліцца або ёсць падзельны на мнагасклад , калі астача ад дзялення мнагаскладаў роўная нулю, , г.зн. мае месца выяўленне . Лік  называецца коранем або нулём мнага-складу , калі .

Мае месца

Крытэр (Безу або падзельнасці мнагаскладу на двухсклад). Для таго каб мнагасклад ненулявой ступені  быў падзельны на двухсклад , неабходна і дастаткова, каб лік  быў коранем мнагаскладу .

□ Неабходнасць. Няхай дзеліцца на , г.зн.  Пры  маем . Гэта азначае, што лік  ёсць корань мнагаскладу .

   Дастатковасць. Няхай  ёсць корань мнагаскладу , г.зн. . На падставе тэарэмы пра выяўленне мнагаскладу , а з прычы-ны таго, што ступень астачы  ёсць меншая за ступень дзельніка , вынікае, што  г.зн.  Нададзім у гэтай роўнасці зменнай  значэнне  і атрымаем, што . Паколькі , то астача , што азначае падзельнасць мнагаскладу  на . ■

Заўвага 1. З доказу тэарэмы вынікае, што  ёсць астача ад дзялення  на .

У трэцім семестры будзе даказана так званая

Асноўная тэарэма алгебры. Усякі мнагасклад ненулявой ступені мае прынамсі адзін корань.

З гэтай тэарэмы вынікае

Тэарэма 2 (пра раскладанне мнагаскладу на множнікі). Усякі мнагасклад  ступені  раскладаецца ў здабытак – го множніка

 .                           (2)

□ З асноўнай тэарэмы алгебры вынікае, што  мае корань , г.зн. . Затым мнагасклад  таксама мае корань г.зн.  і г.д. Нарэшце атрымаем , прычым . Такім чынам, маем .  ■

Тэарэма 3 (пра колькасць каранёў мнагаскладу). Мнагасклад ступені  мае роўна  каранёў.

□ З папярэдняй тэарэмы вынікае, што іх не менш, чым . Няхай разам з каранямі  маецца корань , які не супадае з астатнімі. Гэта значыць, што . Але ж , бо  і ўсе дужкі таксама няроўныя нулю ?!?  (Прыйшлі да супярэчнасці).   ■

Тэарэма 4 (пра камплексныя карані мнагаскладу з рэчаіснымі каэфіцыентамі). Калі мнагасклад  мае рэчаісныя каэфіцыенты і лік  ёсць яго корань, то і лік  – таксама яго корань .

□ Няхай , тады . Але

.

Гэта азначае, што лік  ёсць корань мнагаскладу . ■

Няхай мнагасклад  мае выяўленне . Можа стацца, што сярод яго каранёў ёсць аднолькавыя. Напрыклад, . Запішам мнагасклад  наступным чынам

.                  (3)

def: Лік  называецца коранем мнагаскладу   кратнасці , калі мае месца выяўленне  

Заўвага 2. Калі  ёсць  корань кратнасці  мнагаскладу з рэчаіснымі каэфіцыентамі, то і лік  – таксама яго корань кратнасці .

Калі мнагасклад  мае рэчаісныя каэфіцыенты і  – яго камплексны корань, то ў выяўленні (2) будуць змяшчацца два множнікі  і . Вылічым іх здабытак

, прычым дыскрымінант апошняга трохскладу ёсь , бо . З гэтых меркаванняў на падставе (3) мнагасклад  з рэчаіснымі каэфіцыентамі заўсёды можна падаць у выглядзе

,                     (4)

дзе 

Такім чынам, ведаючы ўсе карані мнагаскладу з рэчаіснымі каэфіцыентамі , можна яго раскласці на множнікі з рэчаіснамі каэфіцыентамі, г.зн. падаць у выглядзе (4), дзе лікі – рэчаісныя, а ўсе квадратовыя трохсклады маюць адмоўныя дыскрымінанты.

def: Рацыянальнай функцыяй называецца выраз , дзе – мнагасклады адпаведна ступеняў  і . Калі , то рацыянальная функцыя называецца правільнай. Правільныя рацыянальныя функцыі   называюцца простымі дробамі.  

Мае месца

Тэарэма 5 (пра раскладанне рацыянальнай функцыі на простыя дробы). Няхай – правільная рацыянальная функцыя з рэчаіснымі каэфіцыентамі і мнагасклад  раскладаецца на множнікі згодна з формулаю (4). Тады функцыю  можна раскласці на суму простых дробаў:

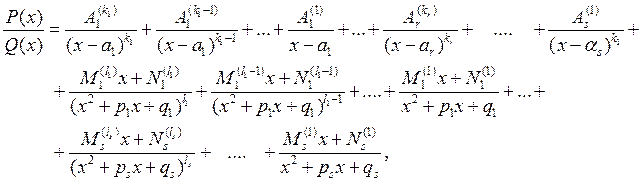
дзе – рэчаісныя лікі.

Тое ж самае можна запісаць пры дапамозе знакаў сумавання

.

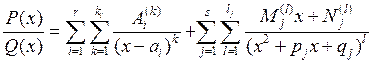Існуе некалькі спосабаў вылічэння каэфіцыентаў раскладу правільнай рацыянальнай функцыі на суму простых дробаў.

1^о. Спосаб адпаведных каэфіцыентаў.

Прыраўноўваючы каэфіцыенты пры аднолькавых ступенях  у мнагаскладаў з лічнікаў абедзвюх частак, прыходзім да сістэмы

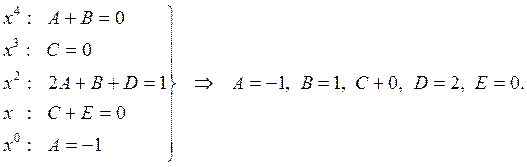
2^о. Спосаб дамнажэння. . Дамножым абедзве часткі на , атрымаем . Беручы ў абедзвюх частках гэтай роўнасці  (– корань двухскладу ), маем . Аналагічна

3^о. Спосаб прыватных значэнняў. .

Спачатку метадам дамнажэння вылічым   Пасля гэтага возьмем у роўнасці значэнне  (адвольны лік, не роўны корню назоўніка рацыянальнай функцыі) і атрымаем .