Уводзіны. Элементы тэорыі мностваў і матэматычнай логікі. Рэчаісныя лікі, страница 4

Заўвага 1. Для неабмежаванага зверху [знізу] мноства  будзем пісаць

Зразумела, што згаданыя азначэнні верхняй і ніжняй межаў можна наступным чынам запісаць пры дапамозе матэматычных сымбаляў:

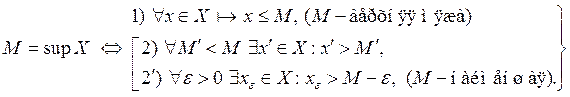
Тэарэма (пра межы). Кожнае непустое абмежаванае зверху [ знізу ]  мноства                                       рэчаісных лікаў мае дакладную верхнюю [ ніжнюю]  мяжу.

□ (без доказу) ■

def: Модулем рэчаіснага ліку  называецца неадмоўны лік :

Асноўныя ўласцівасці модуля:

1)  ;

2) 

3) 

4) 

5)    ( няроўнасць трохвугольніка);

6)    ( у прыватнасці   );

7)  ;

8) 

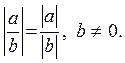
Доказ уласцівасці 5).

З уласцівасці 3) маем ,  адкуль вынікае .  На падставе ўласцівасці 4)  гэта азначае .■

Доказ уласцівасці 6).

Разгледзім роўнасць , якая праўдзіцца . Згодна з уласцівасцю 5) , адкуль вынікае няроўнасць

.                                                                 (5)

Паколькі , то з (5) вынікае

.                                                      (6)

З няроўнасцяў (5) і (6) і вынікае ўласцівасць . ■

Заўвага 2. Часта ў якасці азначэння абмежаванага мноства выкарыстоўваюць наступнае:

def: Калі існуе такі лік , што для ўсіх  выконваецца няроўнасць , то мноства называецца абмежаваным. Тут – верхняя мяжа,  – ніжняя мяжа.

Практыкаванне. Карыстаючыся правіламі дэ Моргана, сфармуляваць азначэнне неабмежаванага мноства. ()

§1.3. Камплексныя лікі.

def: Камплексным лікам  будзем называць упарадкаваную пару рэчаісных лікаў . Пры гэтым  называецца рэчаіснаю, а  – уяўнаю часткаю камплекснага ліку  і абазначаюцца адпаведна . Мноства камплексных лікаў  ёсць .

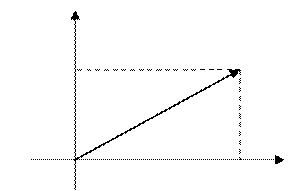
Камплексны лік  геаметрычна выяўляецца як пункт  з каардынатамі  у прамавугольнай дэкартавай сыстэме каардынатаў, або як радыюс-вектар , праекцыі якога на восі каардынатаў  і  адпаведна роўныя  і . Пры гэтым плоскасць  называецца камплекснаю плоскасцю.

Камплексны лік  атаясамляецца з рэчаісным лікам, г.зн. . Гэта дазваляе разглядаць мноства рэчаісных лікаў як падмноства мноства камплексных лікаў , г.зн. . На камплекснай плоскасці рэчаісныя лікі падаюцца як пункты восі  і таму яе называюць рэчаіснаю воссю. Камплексны лік  называецца ўяўным лікам. Уяўныя лікі на камплекснай плоскасці падаюцца як пункты восі , і таму гэтая вось называецца ўяўнаю воссю. Уяўны лік  называецца ўяўнаю адзінкай і абазначаецца літарай , г.зн. . Чаму роўны лік  ? (=1)

def: Два камплексныя лікі  і   называюцца роўнымі , калі . Камплексны лік  называецца нулём, .

def: Сумаю двух камплексных лікаў  і  называецца камплексны лік . Здабыткам двух камплексных лікаў  і  называецца камплексны лік   .

Вылічым , г.зн. . Гэта азначае, што выраз  пры  мае нулявое значэнне, або што раўнанне  мае развязак . Затым вылічым здабытак рэчаіснага ліку на ўяўную адзінку  – атрымаўся ўяўны лік. З гэтай прычыны ўяўны лік  абазначаюць . Мае месца наступнае пераўтварэнне . Па гэтай прычыне камплексны лік  падаецца ў выглядзе , які называецца алгебраічнаю формаю камплекснага ліку.

З алгебраічнай формы камплекснага ліку вынікае правіла: здабытак двух камплексных лікаў можна вылічаць як здабытак мнагаскладаў, замяняючы пры гэтым  на . Сапраўды,

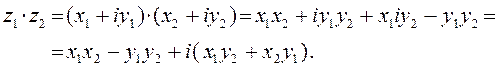
def: Камплексны лік  называюць  розніцаю лікаў  і , , калі . З гэтага азначэння вынікае, што . Чаму?

def: Камплексны лік  называецца камплексна-спалучаным  ліку  і абазначаецца   Відочныя наступныя ўласцівасці камплексна-спалучаных лікаў:  

def: Дзеллю ад дзялення ліку  на лік  называецца такі камплексны лік , які праўдзіць роўнасць                                                          .                         (1)

Пры гэтым дзель абазначаюць  або .

Пераканаемся, што пры ўсіх  і  , калі, раўнанне (1) мае адзіны развязак. Сапраўды, памножым абедзве часткі роўнасці (1) на лік  і атрымаем раўнанне

, раўназначнае раўнанню (1). Пасля перамнажэння камплексных лікаў атрымаем

.

Падзелім гэтую роўнасць на  і заменім  на , атрымаем

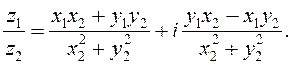                                                        (2)

што і даказвае адзінасць развязка раўнання (1). Пры гэтым мы прыходзім да магчымасці надаць формуле (2) вылічэння дзелі камплексных лікаў выгляд: