Часта сустракаюцца задачы наступнага тыпу:
даказаць праўдзівасць сцверджання ![]() . Пры
гэтым карыстаюцца метадам матэматычнай індукцыі – сцверджанне
. Пры
гэтым карыстаюцца метадам матэматычнай індукцыі – сцверджанне ![]() лічаць праўдзівым для ўсіх
лічаць праўдзівым для ўсіх ![]() , калі выконваюцца наступныя
дзве ўмовы: 1) выказванне
, калі выконваюцца наступныя
дзве ўмовы: 1) выказванне ![]() праўдзівае
пры
праўдзівае
пры ![]() ; 2) з праўдзівасці
выказвання
; 2) з праўдзівасці
выказвання ![]() вынікае праўдзівасць
выказвання
вынікае праўдзівасць
выказвання ![]() для ўсіх натуральных k. Умова праўдзівасці выказвання
для ўсіх натуральных k. Умова праўдзівасці выказвання ![]() называецца базай
індукцыі (часцей за ўсё
называецца базай
індукцыі (часцей за ўсё ![]() ), а
меркаванне праўдзівасці выказвання
), а
меркаванне праўдзівасці выказвання ![]() – індуктыўным
пагадненнем.
– індуктыўным
пагадненнем.
Прыклад. Дакажам,
што ![]() . Пры
. Пры ![]() маем
маем ![]() . Калі ж гэта вам не зусім
падабаецца, то пры
. Калі ж гэта вам не зусім
падабаецца, то пры ![]() маем
маем ![]() . Няхай пры
. Няхай пры ![]() выраз
выраз ![]() і дакажам, што
і дакажам, што ![]() . Сапраўды,
. Сапраўды,
![]() .
Сцверджанне даказана. Зразумела, што тое самае можна атрымаць, калі запісаць
.
Сцверджанне даказана. Зразумела, што тое самае можна атрымаць, калі запісаць ![]() .
.
Пасля ўвядзення мноства цэлых лікаў ![]() робіцца магчымай аперацыя
адымання
робіцца магчымай аперацыя
адымання ![]() лікаў з
лікаў з ![]() . У мностве рацыянальных
лікаў
. У мностве рацыянальных
лікаў ![]() магчымымі
становяцца ўсе 4 арыфметычныя дзеянні.
магчымымі
становяцца ўсе 4 арыфметычныя дзеянні.
Лікавай воссю называюць прамую, на якой выбраны пэўны пункт ![]() (пачатак адліку), маштабны
адрэзак
(пачатак адліку), маштабны
адрэзак ![]() (даўжыня яго лічыцца роўнай
1) і дадатны кірунак ад
(даўжыня яго лічыцца роўнай
1) і дадатны кірунак ад ![]() да
да ![]() .
.
Узнікае задача аб магчымасці паставіць у
адпаведнасць кожнаму пункту ![]() лікавай
восі пэўны лік, які вызначае даўжыню адрэзку
лікавай
восі пэўны лік, які вызначае даўжыню адрэзку ![]() .
Гэты лік будзем лічыць дадатным, калі
.
Гэты лік будзем лічыць дадатным, калі ![]() і
і
![]() знаходзяцца па адзін бок ад
знаходзяцца па адзін бок ад ![]() , і адмоўным – у процілеглым
выпадку.
, і адмоўным – у процілеглым
выпадку.
Адзначым, што пры гэтым кожнаму рацыянальнаму
ліку ![]() адпавядае на лікавай восі
пэўны пункт. Сапраўды, мы ведаем спосаб пабудовы адрэзку, даўжыня якога складае
адпавядае на лікавай восі
пэўны пункт. Сапраўды, мы ведаем спосаб пабудовы адрэзку, даўжыня якога складае
![]() частку даўжыні адрэзку
частку даўжыні адрэзку ![]() ,
, ![]() (тэарэма Фалеса).
Адкладаючы гэтую
(тэарэма Фалеса).
Адкладаючы гэтую ![]() -ю частку
-ю частку ![]() разоў, мы атрымаем пункт
разоў, мы атрымаем пункт ![]() , які знаходзіцца на
адлегласці
, які знаходзіцца на
адлегласці ![]() ад О. Такім чынам, пункту
ад О. Такім чынам, пункту ![]() адпавядае рэчаісны лік
адпавядае рэчаісны лік ![]() .
.
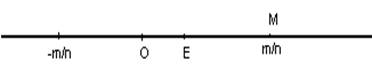
Аднак не кожнаму пункту лікавай
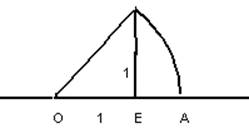
восі адпавядае рацыянальны лік. Дзеля доказу гэтага сцверджання разгледзім
пункт ![]() на лікавай восі такі, што
даўжыня адрэзку роўная даўжыні дыяганалі квадрату са стараною
на лікавай восі такі, што
даўжыня адрэзку роўная даўжыні дыяганалі квадрату са стараною ![]() . Відочна
. Відочна ![]() 2 =2.
2 =2.
Пераканаемся, што пункту ![]() не
адпавядае ніякі рацыянальны лік.
не
адпавядае ніякі рацыянальны лік.
□ (Ад процілеглага) Няхай |![]() |
=
|
=![]() – нескарачальны дроб. Тады
– нескарачальны дроб. Тады ![]() , г.зн. што лік
, г.зн. што лік ![]() ёсць цотны, а тым самым р –
цотны. Няхай
ёсць цотны, а тым самым р –
цотны. Няхай ![]() . Маем
. Маем ![]() , г.зн.
, г.зн. ![]() – цотны лік ?!? (знак
супярэчнасці) ■
– цотны лік ?!? (знак
супярэчнасці) ■
Узнікае неабходнасць пашырэння мноства
рацыянальных лікаў. Няцяжка пераканацца, што кожны рацыянальны лік можна падаць
як бясконцы перыядычны дзесятковы дроб. (Падумаць самастойна або паглядзець
літаратуру!) І наадварот, кожны бясконцы перыядычны дзесятковы дроб ёсць
рацыянальны лік, г.зн. яго можна падаць у выглядзе ![]() .
(Як пераўтварыць бясконцы перыядычны дзесятковы дроб у звычайны?) Такім чынам,
мноства бясконцых перыядычных дзесятковых дробаў ёсць
.
(Як пераўтварыць бясконцы перыядычны дзесятковы дроб у звычайны?) Такім чынам,
мноства бясконцых перыядычных дзесятковых дробаў ёсць ![]() .
.
Бясконцыя неперыядычныя дзесятковыя дробы называюцца ірацыянальнымі
лікамі. Аб’яднанне мностваў рацыянальных ![]() і
ірацыянальных лікаў
і
ірацыянальных лікаў ![]() называюць мноствам
рэчаісных лікаў і абазначаюць
называюць мноствам
рэчаісных лікаў і абазначаюць ![]() .
.
Такім чынам, маем ![]() .
.
Няхай два рэчаісныя лікі ![]() і
і
![]() маюць выяўленні:
маюць выяўленні: ![]() ,
,
![]() . Лікі
. Лікі ![]() і
і ![]() называюцца роўнымі, калі
называюцца роўнымі, калі ![]() . Калі дзесятковыя знакі лікаў
. Калі дзесятковыя знакі лікаў ![]() і
і ![]() адпавядаюць умовам:
адпавядаюць умовам: ![]() ,
то лік
,
то лік ![]() называецца меншым за
лік
называецца меншым за
лік ![]() . У выпадку
. У выпадку ![]() мае
месца дамоўленасць:
мае
месца дамоўленасць: ![]() .
.
Адзначым дзве важныя надалей ўласцівасці рэчаісных лікаў:
1º.(Аксіёма Архімеда) ![]() (тут
(тут ![]() – мноства дадатных
рэчаісных лікаў);
– мноства дадатных
рэчаісных лікаў);
2º.(Шчыльнасць мноства ![]() )
) ![]() .
.
Сярод найбольш ужываных мностваў рэчаісных лікаў назавем:
![]() – адрэзак
(замкнёны прамежак);
– адрэзак
(замкнёны прамежак);
![]() – інтэрвал
(адкрыты прамежак).
– інтэрвал
(адкрыты прамежак).
def: Адвольны інтэрвал ![]() ,
якому належыць пункт
,
якому належыць пункт ![]() , будзем называць ваколлем
пункта
, будзем называць ваколлем
пункта ![]() . Сіметрычнае ваколле, г.зн. інтэрвал
. Сіметрычнае ваколле, г.зн. інтэрвал ![]() (
(![]() ) называюць
) называюць ![]() -акругаю пункта
-акругаю пункта ![]() .
.
def: Мноства ![]() называецца
абмежаваным зверху [знізу], калі
называецца
абмежаваным зверху [знізу], калі ![]() рэчаісны лік
рэчаісны лік ![]() такі, што
такі, што ![]() . Лікі
. Лікі ![]() і
і ![]() называюць адпаведна верхняйі ніжняй межамі мноства
называюць адпаведна верхняйі ніжняй межамі мноства ![]() .
Мноства, абмежаванае як зверху, так і знізу называецца абмежаваным.
.
Мноства, абмежаванае як зверху, так і знізу называецца абмежаваным.
Практыкаванне Карыстаючыся правіламі дэ Моргана, сфармуляваць азначэнне неабмежаванага зверху [знізу] мноства.
( ![]()
![]() ,
[
,
[![]()
![]() ] )
] )
Відочна, што ўсякае абмежаванае мноства мае бясконца многа як верхніх, так і ніжніх межаў. Чаму? (аксіёма Архімеда!)
def: Найбольшая з ніжніх межаў абмежаванага знізу
мноства ![]() называецца яго дакладнай
ніжняй мяжою і абазначаецца
называецца яго дакладнай
ніжняй мяжою і абазначаецца ![]() (чытаецца:
інфімум).
(чытаецца:
інфімум).
def: Найменшая з верхніх межаў абмежаванага зверху
мноства ![]() называецца яго дакладнай
верхняй мяжою і абазначаецца
называецца яго дакладнай
верхняй мяжою і абазначаецца ![]() (чытаецца:
супрэмум).
(чытаецца:
супрэмум).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.