Уводзіны. Элементы тэорыі мностваў і матэматычнай логікі. Рэчаісныя лікі, страница 2

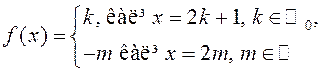
адлюстроўвае мноства  на мноства  узаемна адназначна. Такім чынам, .

Мноства  называецца злічальным, калі  і незлічальным, калі яно бясконцае і не ёсць злічальным.  Мноства  ёсць злічальнае мноства.

У матэматыцы побач з паняццямі тэорыі мностваў шырока выкарыстоўваецца мова матэматычнай логікі, аснову якой складае тэорыя выказванняў. Выказванне як і мноства ёсць першаснае неазначальнае паняцце. Выказваннемлічыцца ўсякі сказ, пра які можна сказаць, што яго сцверджанне ёсць або праўдзівае, або непраўдзівае. Так выказваннямі з’яўляюцца наступныя сцверджанні: “Калі чатырохвугольнік ёсць квадрат, то ён прамавугольнік”– праўдзівае сцверджанне. “Калі чатырохвугольнік ёсць прамавугольнік, то ён квадрат”– непраўдзівае сцверджанне. “Пад час лекцыі па матэматычным аналізе заўсёды свеціць сонца”.– непраўдзівае.

Імплікацыяйвыказванняў  і  называецца выказванне, якое ёсць непраўдзівае калі і толькі калі  праўдзівае, а  непраўдзівае, і абазначаецца  (чытаецца: “калі  , то ” ). Выказванне  чытаюць таксама: “з  вынікае ”, “для таго каб , дастаткова ”, “для таго каб , неабходна ”. Пры гэтым  называюць умовай, а  – высновай . Кажуць таксама, што  ёсць дастатковая ўмова для , а  ёсць неабходная ўмова для  .

Прыклад 4. : “Чатырохвугольнік ёсць ромб”;  :“Чатырохвугольнік ёсць паралелаграм”. Маем , г. зн.:

1. Для таго каб чатырохвугольнік быў ромбам, неабходна, каб ён быў паралелаграмам.

2. Для таго каб чатырохвугольнік быў паралелаграмам, дастаткова, каб ён быў ромбам. ◄

Калі для выказванняў  і  маюць месца імплікацыі  і , то выказванні  і  называюць эквівалентнымі або раўназначнымі і пішуць . Выказванне  чытаюць таксама: “Для таго каб , неабходна і дастаткова каб ”, “ калі і толькі калі ”. Тэарэмы з такімі выказваннямі будзем называць крытэрамі.

Прыклад 5. : “Трохвугольнік ёсць раўнабочны”; : “Два вуглы трохвугольніка роўныя”. Маем , , г. зн. . Такім чынам, маюць месца сцверджанні: “Для таго каб трохвугольнік быў раўнабочным, неабходна і дастаткова, каб два яго вуглы былі роўныя”, або “Для таго каб два вуглы трохвугольніка былі роўныя, неабходна і дастаткова, каб трохвугольнік быў раўнабочным”. Тое ж самае можна сфармуляваць пры дапамозе іншых слоў:“Трохвугольнік ёсць раўнабочны, калі і толькі калі два яго вуглы роўныя”, або :“ Два вуглы трохвугольніка роўныя, калі і толькі калі ён раўнабочны”. ◄

У матэматыцы апроч выказванняў сустракаюцца сцверджанні, якія залежаць ад адной або некалькіх зменных. У матэматычнай логіцы іх называюць прэдыкатамі і абазначаюць  і г.д. Пры гэтым абавязкова адзначаецца, на якім мностве разглядаюцца зменныя. Сказ “” не з’яўляецца выказваннем на ўсім мностве . Але калі ўзяць , то  – выказванне. З мноства  можна вылучыць падмноства  усіх тых , для якіх  ёсць праўдзівае. Мноства  называецца мноствам праўдзівасці сцверджання . Тады на мностве  сцверджанне  непраўдзівае.

З прэдыкатамі спалучаюцца два віды сказаў: 1)  Для ўсіх  з мноства  мае месца . 2)  Існуе элемент  з мноства такі, што мае месца.

Гэтыя сказы можна запісаць кароткім спосабам: 1)  2) .

Знакі  называюцца квантарам агульнасці і квантарам  існавання адпаведна.

Квантар  замяняе словазлучэнні: “для ўсіх”, “для кожнага”.

Квантар  замяняе словазлучэнні: “існуе”, “знойдзецца”.

Сымбаль  азначае: “мае месца”, а сымбаль  : – “такі, што”.

    Адмаўленнем выказвання  называецца выказванне  (чытаецца: “не ”), якое праўдзіцца калі і толькі калі  непраўдзівае. Так выказванне “5 ёсць цотны лік” з’яўляецца адмаўленнем выказвання “5 ёсць няцотны лік”.

Разгледзім правілы пабудовы адмаўленняў некаторых сцверджанняў.

1º. Няхай мае месца сцверджанне: “”. Тады яго адмаўленнем  з’яўляецца сцверджанне: “не для кожнага элемента  з мноства  мае месца ”, або інакш “існуе элемент  з мноства  такі, што мае месца ”. Такім чынам, маем     .

2º. Аналагічна атрымліваецца.

Атрыманыя правілы пабудовы адмаўленняў называюць правіламі дэ Моргана пабудовы адмаўлення.

§1.2.  Рэчаісныя лікі.

Пры падлічэнні колькасці элементаў розных мностваў узнікае мноства натуральных лікаў . З натуральнымі лікамі можна выконваць дзеянні складання і множання. Аперацыі адымання і дзялення не заўсёды магчымыя.