Министерство Образования РФ
САНКТ – ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ
Лабораторная работа №2
МОДЕЛИРОВАНИЕ ЭЛЕКТРОГИДРАВЛИЧЕСКОЙ СЛЕДЯЩЕЙ СИСТЕМЫ
Выполнил: Проверил:
Студент группы 541
Санкт-Петербург
2005 г.
I Идеальное реле
При малых Т2 мы получаем колебательный процесс, точка С совпадает с координатой движка, фазовая траектория имеет вид слабосходящейся спирали.
Время переходного процесса равно tпп=1,001 c
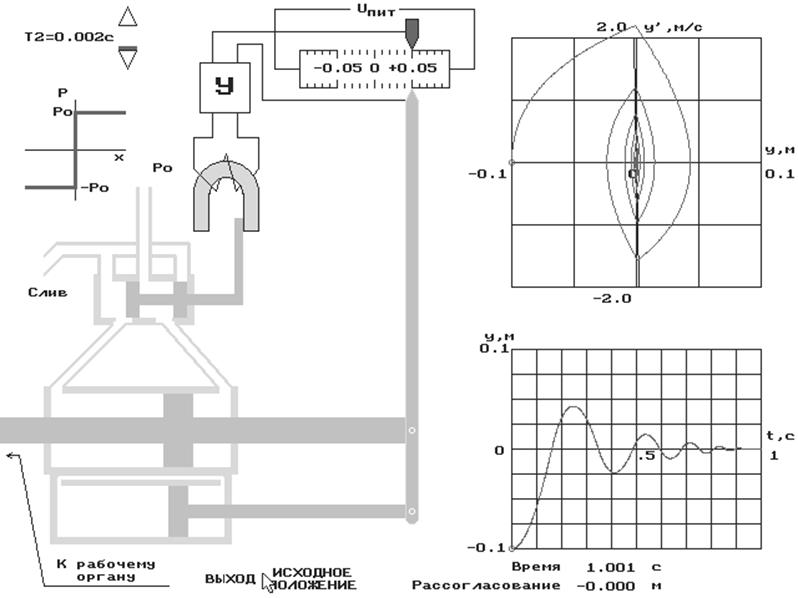
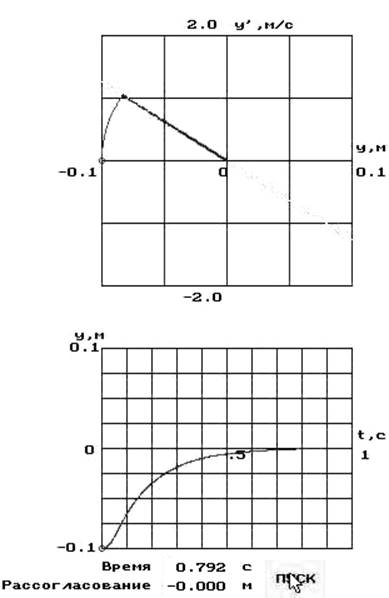
Получаем максимальное подтормаживание нижней точки. Верхняя часть рычага будет опережать точку С. Скользящий режим сопровождается быстрым переключением золотниковой схемы. На практике частые перемещения приведут к отказу системы.
Время переходного процесса равно tпп=0,792 c
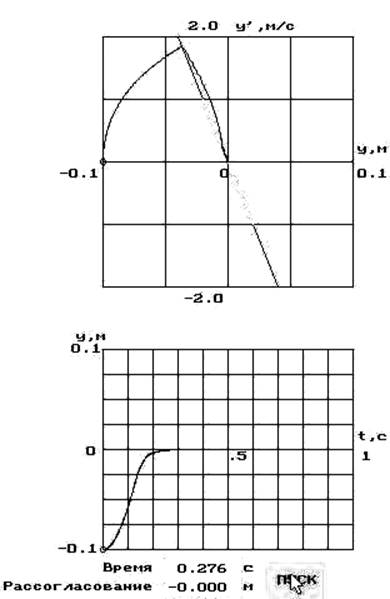
|
Т2, с |
tпп, с |
|
0,05 |
0,352 |
|
0,04 |
0,276 |
|
0,03 |
0,318 |
Оптимальное значение tпп = 0,276 при Т2 = 0,04 с
II Гистерезис
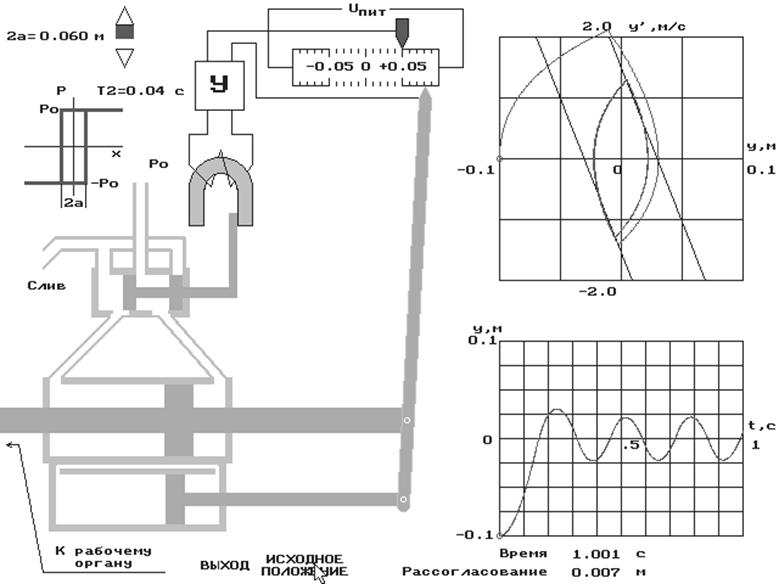
2а = 0,060 – max
Т2 = 0,04 const
Uпит = max
Получаем процесс незатухающих колебаний, поэтому процесс равновесия не достигается. В фазовой плоскости точка движется по замкнутому циклу. Амплитуда тем больше, чем больше ширина зоны гистерезиса.
2а = 0,040 – min
Т2 = 0,04 const
Uпит = max
При минимальном коэффициенте 2а амплитуда меньше ошибки, но также присутствуют автоколебания, что приведет к отказу системы.
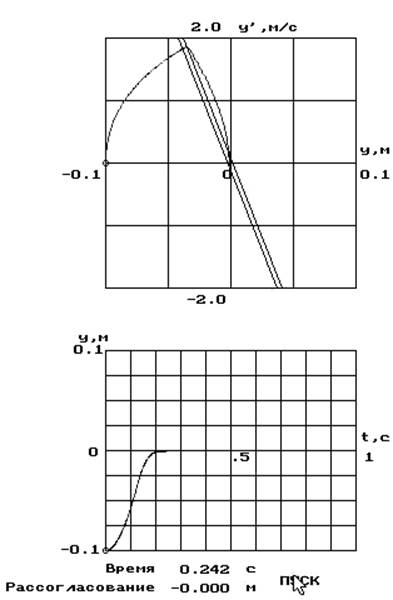
III Зона нечувствительности
Чтобы избавиться от автоколебаний в систему вводится зона нечувствительности.
1. Задаем: а = 0,060 – max
Т = const
Рассогласование 0,016 м.
Ошибку ожидаем ± а.
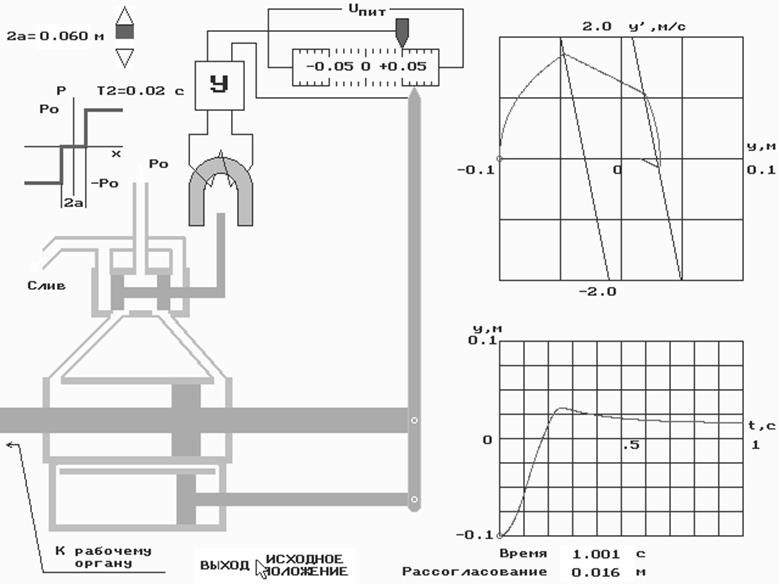
2. Задаем:
а = 0,002
Т = 0,25
Рассогласование 0,001
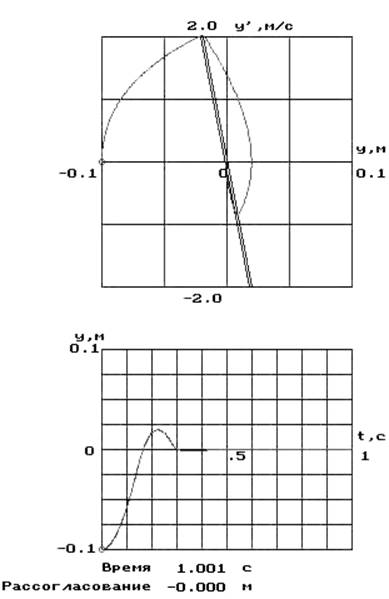
Следовательно, нужно выбирать зону нечувствительности так, чтобы она покрывала зону гистерезиса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.