Решение задачи линейного программирования. Прибыль от реализации предприятием одного изделия каждого вида

Министерство Образования РФ

Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров

Кафедра  АТЭП

КУРСОВАЯ  РАБОТА

по дисциплине: «Основы теории принятия решения»

Вариант №63

Выполнила:                                                                                                           студентка гр.544    

 

Проверил:                                                                                                                                                             

Санкт – Петербург

2007г.

Содержание

1.  Постановка задачи………………………………………………………………3

2.  Решение задачи линейного программирования……………………………4

3.  Вывод…………………………………………………………………………….6

Постановка задачи:

На предприятии разрабатывается план производства 3-х видов изделий, изготовление которых может выполняться на 3-х типах станков.

Выделяемое для производства количество станков по типам и производительность одного станка каждого типа по видам изделий представляется в таблице 1 (при невозможности использования станка для производства какого-либо изделия в соответствующей клетке ничего не записывается).

Известна прибыль от реализации предприятием одного изделия каждого вида (данные приведены в нижней строке таблицы 1).

Требуется произвести распределения выделенных станков для производства планируемых к выпуску изделий с тем, чтобы обеспечивать получения максимальной прибыли. Исходя из этого, определить количество производимых изделий каждого вида.

Таблица 1.

Типы количества станков по типам		Виды изделий
		B1	B2	B3
T1	6	1	1	5
T2	4	2	1	-
T3	4	2	-	1
Прибыль		60	40	70
Задания		>=10	<=10	>=10

Решение задачи линейного программирования.

Обозначим через  количество станков каждого типа по изготовлению изделий каждого вида, где i – количество типов станков,

j – количество видов изделий.

Составим целевую функцию исходя из условий задачи:

 → max.

Введем ограничения:

- по количеству выделенных станков:

       

   

         

- по количеству выделенных изделий каждого вида на всех типах станков:

           

             

           

- граничные условия:

;;;;;;;;;

Тогда математическая модель данной задачи будет иметь вид:

            

          

;;;;;;;;;

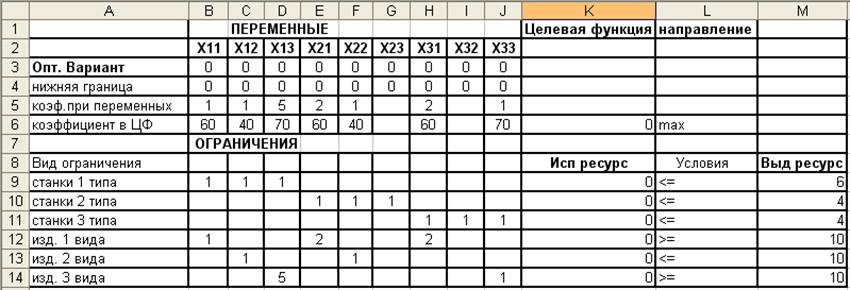
Таблица исходных данных:

Расчет оптимального решения:

·  Вводим исходные данные в составленную нами таблицу:

В строке 2 записываем обозначения искомых переменных. В соответствующих  клетках строки 3 представим их значения в оптимальном варианте решения, которые первоначально записываются нулями. В строке 4 записываем граничные условия переменных, т.е. нули, вследствие их неотрицательности. В строках 5 и 6 записываются коэффициенты при переменных и при ЦФ. Ниже в соответствующих строках записываем коэффициенты при переменных из условий ограничений по станкам и по изделиям, их выделенные значения и используемые значения при оптимальном решении. В клетку L6 целесообразно записать для наглядности направление изменения целевой функции, т.е. max. В клетке K6 будет записано значение целевой функции.

·  Производим расчет:

1.  Значения ЦФ и ограничений мы считаем через функцию СУММПРОИЗВ, куда мы вводим соответствующие массивы.

2.  Для определения оптимального решения мы используем «поиск решений»:

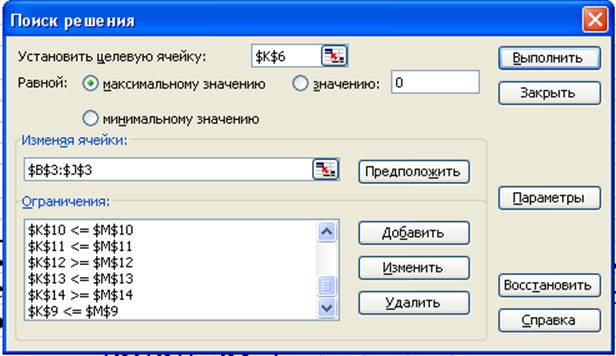, куда мы вводим ячейку с ЦФ, ограничения и массив переменных, который нужно определить. Также мы устанавливаем флажок «max» и в «параметрах» - «линейная модель».

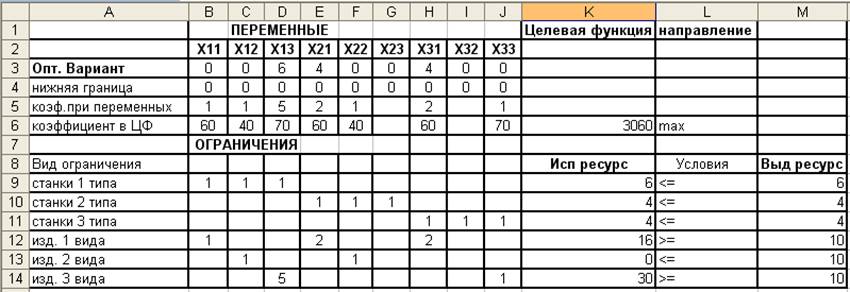
Таблица после нахождения оптимального решения:

Вывод

Из таблицы видно, что выделенные ресурсы используются на 100%. Изделия  второго вида выпускать не целесообразно.

Станок 1 – 3 вид изделия;

Станок 2 – 1 вид изделия;

Станок 3 – 1 вид изделия;

Наибольшая прибыль составляет: 3060 ед.