



5. Волны
5.1 Распространение продольной волны в стержне
Вопрос о распространении упругой волны рассмотрим на примере продольных колебаний длинного стержня постоянного сечения:
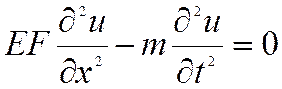 или
или 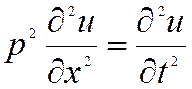 , где .
, где .
Будем искать частное решение в форме ![]() , где функция
, где функция ![]() должна
быть дважды дифференцируемой и по x , и по t.
должна
быть дважды дифференцируемой и по x , и по t.
Имея ввиду правила дифференцирования сложной функции
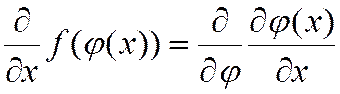
запишем выражения для частных производных:
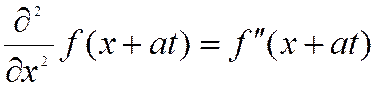 и
и 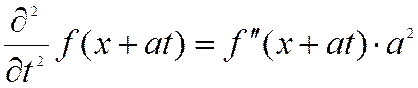 .
.
Здесь двумя штрихами обозначено двойное дифференцирование по
аргументу ![]() .
.
Подставляя полученные выражения в уравнение ……, получаем
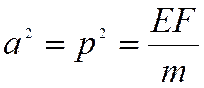 ,
откуда следует
,
откуда следует 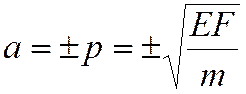 .
.
Таким образом общее решение однородного уравнения свободных колебаний принимает вид
![]() .
.
В такой форме решение принадлежит Даламберу.
Для определения функций ff воспользуемся начальными условиями, которыми задается состояние стержня в начальный момент времени t=0. Пусть внешнее малое возмущение прикладывается к стержню в точке x=0 в момент времени t=0
![]()
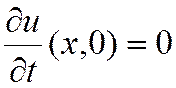 .
.
Тогда
![]() ;
;
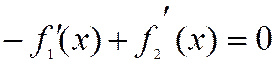 .
.
Проинтегрируем второе уравнение по х:
![]() .
.
Решая уравнения относительно функций получаем
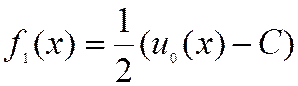
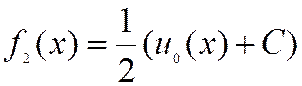
После замены аргумента на ![]() и
на
и
на ![]() решение принимает вид:
решение принимает вид:
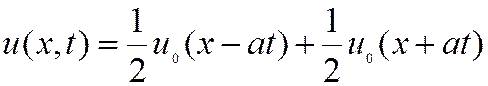
Рассмотрим такой стержень, получивший в начальный момент времени возмущение, представленное графически на рис.
Построим графики первого и второго слагаемых по отдельности
(, а затем вместе,) в моменты времени 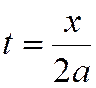 и
и
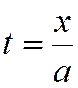 , а затем – в произвольный момент
времени t рис….
, а затем – в произвольный момент
времени t рис….
Очевидно, что функции ![]() и
и
![]() не изменят своих значений, если не
произойдет изменения аргументов:
не изменят своих значений, если не
произойдет изменения аргументов:
![]() ,
,
![]() .
.
Следовательно, при изменении времени на dt
кривые ![]() и
и ![]() переместятся,
соответственно, в положительном направлении и в отрицательном направлении оси х на adt. При этом скорость
перемещения равна а – скорость
распространения волн (в частности, звуковых) в материале (скорость звука):
переместятся,
соответственно, в положительном направлении и в отрицательном направлении оси х на adt. При этом скорость
перемещения равна а – скорость
распространения волн (в частности, звуковых) в материале (скорость звука): 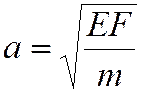
Решение определено только условиями начала движения и не зависит от граничных условий. Оно справедливо только для бесконечно длинного стержня.
Решение можно использовать и для стержней конечной длины, но при этом нужно учесть отражение волн от концов стержня и наложение отраженных волн на основное решение.
5.2 Уравнения движения в безграничном упругом пространстве
Задачи о колебаниях упругих тел ограниченных размеров, решение для которых представлялось в виде разложения по собственным формам, которое также называют решением в стоячих волнах (неизменные во времени).
Понятие о собственных формах колебаний теряет смысл, когда мы имеем дело с упругим телом бесконечных размеров.
· Во-первых, собственные частоты уже более неопределимы (их находят из характеристического уравнения однородной системы уравнений, описывающей граничные условия),
· во-вторых, для реализации колебаний по некоторой форме, описываемой функцией, заданной на бесконечном диапазоне , потребовался бы ввод неограниченного количества энергии.
В телах неограниченных размеров колебания изучаются в рамках волновой теории. Задача ставится следующим образом: упругая среда находится в покое, конечное возмущение создается в некоторой части среды; требуется определить движение точек среды без разложения в бесконечный ряд.
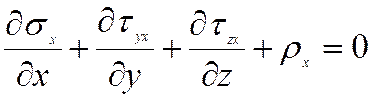
![]() , где
, где 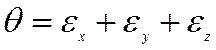 - объемная деформация,
- объемная деформация,
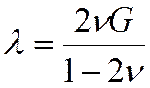 - параметр Ляме.
- параметр Ляме.
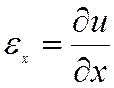 ;
;
Уравнения равновесия, выраженные через перемещения (уравнения Ляме):
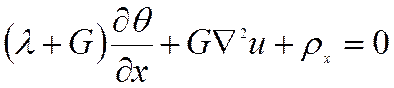 , где
, где 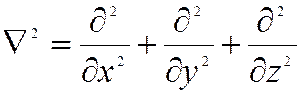 - оператор Лапласа.
- оператор Лапласа.
Если объемные силы представлены силами инерции 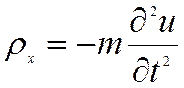 и т.п., то уравнения равновесия
становятся уравнениями движения элементарного объема и приобретают вид:
и т.п., то уравнения равновесия
становятся уравнениями движения элементарного объема и приобретают вид:
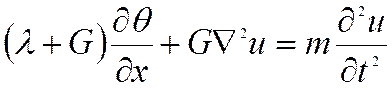
5.3 Распространение плоской волны в неограниченном пространстве
Пусть внешнее возмущение в момент времени t=0 смещением плоскости, перпендикулярной оси х, как жесткого целого, т.е. u0, v0, w0, и соответствующие скорости являются функциями только х .
В уравнениях движения исчезают производные по y и z и они принимают вид
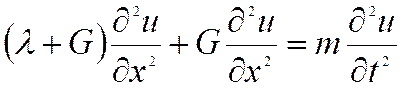
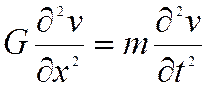
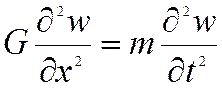
или
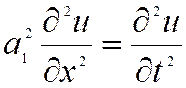 ,
,
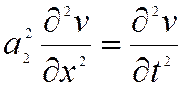 ,
, 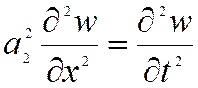
Здесь 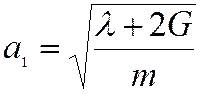 и
и  скорости распространения продольной
и двух поперечных волн.
скорости распространения продольной
и двух поперечных волн.
Общее решение этих уравнений получено Даламбером в виде
![]()
![]()
![]()
Первое уравнение описывает движение продольной волны – волны расширения-сжатия – скорость а1.
Два других уравнения описывают распространение вдоль оси х перемещений, перпендикулярных к оси х – т.е. распространение поперечных волн. Этот процесс имеет аналогичный движению продольной волны характер: прямая и обратная волны распространяются со скоростью а2 и называются также волнами сдвига.
5.4 Волновые уравнения и их решения
Уравнения движения, решение которых имеет вид решения Даламбера, в виде прямой и обратной волны, называются волновыми уравнениями:
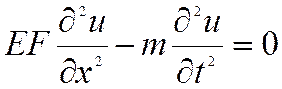 или
или 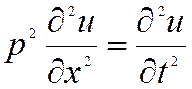 ;
;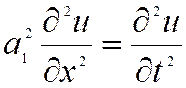 ,
,
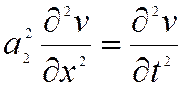 ,
, 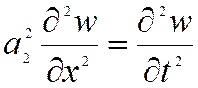 ;
;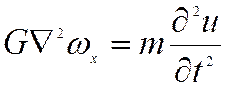 ;
; 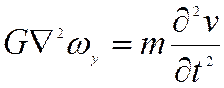 ;
; 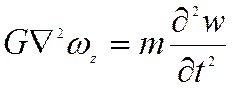 ,
,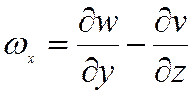 - компоненты вращения
элементарного объема.
- компоненты вращения
элементарного объема.Все эти постановки рассматривают тела бесконечных размеров. Применение полученных решений к телам ограниченных размеров требует учета явлений отражения, преломления и интерференции (наложения) волн.
Волна переносит энергию, а не материю. (чайки)
Все эти постановки предполагают, что функции, входящие в общее решение как минимум дважды дифференцируемы. Следовательно, решение не предполагает разрывов в скоростях и в напряжениях. Волны, несущие разрыва скоростей и напряжений называются ударными волнами. Задача распространения ударных волн требует другой постановки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.