Воспроизведение разгонной кривой по импульсной кривой и аппроксимация разгонной кривой методом моментов переходной функции

Санкт-Петербургский Государственный Технологический

Университет Растительных Полимеров

Кафедра АТЭП

Дисциплина: «Моделирование систем»

Лабораторная работа

Воспроизведение разгонной кривой по импульсной кривой и аппроксимация разгонной кривой методом моментов переходной функции.

Выполнил:                                                                    студент гр.542   

Проверил:                                                                     

Санкт-Петербург

2005

Вариант 72

1.  Тип объекта –статический, так как состояние переходного процесса

после импульсного воздействия, возвращается в установившееся

значение.

	m

Объект       

%                             см

2.  Структура объекта –реальное интегрирущее звено с запаздыванием

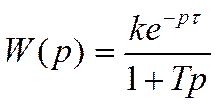
3.  Приближенная оценка параметра объекта:

m0 = 62.5%        m∞ = 52.5%

∆m∞  = m∞ - m0 = 52.5 – 62.5 = - 10(%)

H0 = 125 см        H∞ = 101 см

∆H∞  = H∞ - H0 =101 – 125 = -24

		m				%
	mo
	m∞
		H
	H∞
	Ho
										t, сек

Определяем коэффициент передачи сигнала:

К= ∆H∞/∆m∞ = 24 /10 = 2.4 [см/%]

Постоянная времени Т при t₁= T + τ  и t₂= 2T + τ

Для нахождения Т рассмотрим две точки t1 и t2:

∆H (t₁)  = H0 +  0,63*∆H∞ =125 - 0,63*24 = 109,28 [см]             

∆H (t₂) = H0  +  0,87*∆H∞ =125 - 0,87*24 = 104,12 [см]             

Тогда:

t₁= 280 сек   и   t₂= 330 сек

Запаздывание определяем визуально из графика: τ=20 сек.

t1 + t2 = 3T + 2τ

Отсюда

Т= (t1 + t2 - 2τ)/3= (280 + 330 - 2*140)/3 = 176,67 мин

В итоге получаем:

2.4 * e ^(-40*P)

W(P) = ---------------------1 + 176.67*P

1.

	m  [%]

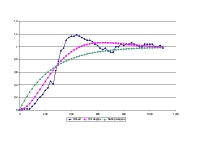
2. Оптимальная модель имеет следующие параметры:

Передаточная функция вида:

K

W(P) = --------------------------  .

1 + 2*Ksi*T*P + T**2*P**2

дисперсия адекватности- σ²ад = 0.012301

3.Выборочная модель имеет следующие параметры:

Передаточная функция:

           K

W(P) =      ---------  .

                1 + T*P

дисперсия адекватности- σ²ад = 0.014213

4. Вывод:

После программного расчета сделан вывод о том, что значение дисперсии адекватности в оптимальной и выборочной модели приблизительно одинаковые, но оптимальная модель более соответствует объекту, поэтому выбираем оптимальную модель.

АППРОКСИМАЦИЯ  РАЗГОННОЙ  КРИВОЙ 

МЕТОДОМ МОМЕНТОВ ПЕРЕХОДНОЙ ФУНКЦИИ

21.12.05

ПАРАМЕТРЫ  ВХОДНОГО ВОЗДЕЙСТВИЯ  :

ЗНАЧЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ ДО ЭКСПЕРИМЕНТА  =    62.500

ЗНАЧЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ В  ИМПУЛЬСЕ =    52.500

ДЛИТЕЛЬНОСТЬ  ИМПУЛЬСА  =   400.000

ПАРАМЕТРЫ  ВЫХОДНОГО СИГНАЛА ОБЪЕКТА  :

СРЕДНЕЕ ЗНАЧЕНИЕ ВЫХОДНОГО СИГНАЛА ДО ОПЫТА  =   125.000

УСТАНОВ.СРЕДН.ЗНАЧ.ВЫХОДНОГО СИГНАЛА ПОСЛЕ ОПЫТА =   101.000

ШАГ ДИСКРЕТНОСТИ ПО ВРЕМЕНИ    =    20.000

ЧИСЛО ТОЧЕК КРИВОЙ РАЗГОНА     = 56

КРИВАЯ  РАЗГОНА

Номер точки   Значение кривой разгона

1             125.000

2             124.500

3             124.500

4             124.500

5             124.500

6             123.500

7             122.500

8             121.000

9             120.000

10             119.000

11             117.500

12             116.500

13             114.000

14             115.000

15             110.000

16             106.500

17             102.500

18             101.500

19              98.500

20              97.500

21              97.000

22              97.000

23              97.000

24              97.500

25              98.000

26              98.500

27             100.000

28             101.000

29             103.000

30             105.000

31             106.500

32             109.000

33             110.500

34             112.500

35             112.500

36             118.000

37             121.500

38             123.500

39             124.500

40             126.500

41             128.000

42             128.000

43             128.000

44             128.000

45             128.000

46             128.000

47             128.000

48             127.500

49             126.500

50             126.000

51             125.000

52             124.500

53             124.500

54             124.000

55             124.000

56             124.000

**********************************************************************

МОДЕЛЬ   С   М И Н И М А Л Ь Н Ы М

ЗНАЧЕНИЕМ ДИСПЕРСИИ АДЕКВАТНОСТИ

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ