4. Определение числовых характеристик нагрузок потребителей
К числовым характеристикам случайных величин относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Математическое ожидание М(h) определим по выражению:
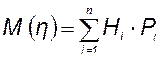 ,
(4.1)
,
(4.1)
где Hi - возможная нагрузка;
Рi - вероятность включения возможной электрической нагрузки.
Подставляем:
М(h)= 0·5,43582·10-5 + 2·1,44955·10-4 + 3·2,71791·10-5 + 4·1,44955·10-4 + +5·7,24776·10-4 + 6·6,78219·10-5 + 7·1,81194·10-3 + 8·3,45946·10-4 + +9·1,77167·10-3 + 10·4,30336·10-3 + 11·8,192331·10-4 + 12·1,00059·10-4 + +13·1,94985·10-3 + 14·9,51939·10-3 + 15·1,49485·10-2 + 16·4,337252·10-3
+17·3,20109·10-2 + 18·6,38407·10-3 + 19·2,94332·10-2 + 20·3,35322·10-2 +
+21·1,31566·10-2 + 22·6,53204·10-2 + 23·1,33732·10-2 + 24·5,74989·10-2 + +25·5,05123·10-2 + 26·2,50491·10-2 + 27·8,80874·10-2 + 28·1,85735·10-2 + +29·7,31842·10-2 + 30·5,13685·10-2 + 31·3,07438·10-2 + 32·7,84796·10-2 +
+33·1,70872·10-2 + 34·6,01677·10-2 + 35·3,43985·10-2 + 36·2,39140·10-2 +
+37·4,46417·10-2 + 38·1,00291·10-2 + 39·3,03726·10-2 + 40·1,41894·10-2 + +41·1,09827·10-2 + 42·1,49060·10-2 + 43·3,40259·10-3 + 44·8,33209·10-3 + +45·3,09587·10-3 + 46·2,47204·10-3 + 47·2,40790·10-3 + 48·5,07378·10-4 + +49·9,17294·10-4 + 51·2,32190·10-4 + 52·1,37594·10-4 + 53·1,03196·10-4 + +54·1,71993·10-5= 28,4 кВт.
В качестве меры отклонения случайной величины от её математического ожидания принимают величину, равную математическому ожиданию квадрата отклонения случайной величины от её математического ожидания, которую называют дисперсией случайной величины h:
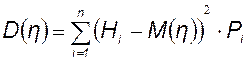 .
(4.2)
.
(4.2)
Подставляем:
D(h) = (0-28,4)2·5,43582·10-5 + (2-28,4)2·1,44955·10-4 + … + (52-28,4)2· ·1,03196·10-4 + (54-28,4)2·1,71993·10-5 = 54,72 кВт.
Квадратный корень из величины дисперсии называется средним квадратическим отклонением случайной величины и определяется по формуле:
![]() .
(4.3)
.
(4.3)
Подставляем значения:
s(h) = ![]() = 7,39 кВт.
= 7,39 кВт.
![]()
Показатель размаха вариации R исчисляют как разность между наибольшим и наименьшим значениями варьирующего признака:
![]() R = Hmax
– Hmin . (4.4)
R = Hmax
– Hmin . (4.4)
Подставляем значения:
R = 54 – 2 = 52 кВт.
Относительной мерой вариации, позволяющей сравнивать степень варьирования признаков в вариационных рядах с разным уровнем средних, является коэффициент вариации, определяемый по выражению:
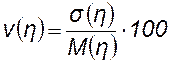 ,
(4.5)
,
(4.5)
где s(h) – среднее квадратическое отклонение;
М(h) – математическое ожидание.
Подставляем значения:
![]() (h) =
(h) = 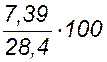 = 26,047
%.
= 26,047
%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.