Проектирование системы электропривода ленточно-цепного конвейера. Технологическое описание механизма и требования его ЭП, страница 4

Т.к. корни характеристического уравнения комплексные, то решение дифферинциального уравнения (2) и (3) будет иметь вид:

Найдём значение коэффициентов А,B,C,D, подставляя в полученные уравнения начальные условия для t=0.

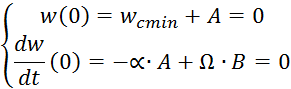
Решая данную систему получим:

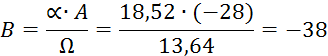
Решая данную систему получим:

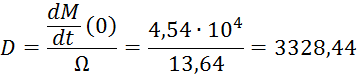
Окончательно получим:

Графическим способом определяем время переходного процесса 2-ого этапа:

Также определяем начальную скорость для 3-го этапа:

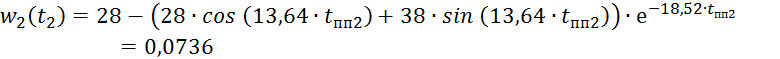
Определим значение скорости после переходного процесса 3-го этапа:

 

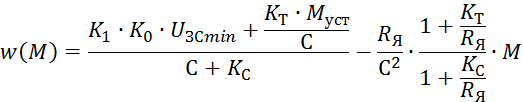
3 этап

 

Включается обратная связь по току ().

Дифферинциальные уравнения относительно скорости и момента составленные по системе уравнений (*) имеют вид:

- по скорости

-по моменту

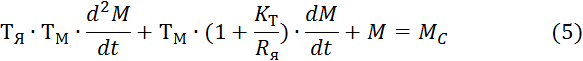
Найдём начальные условия:

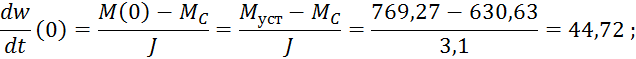
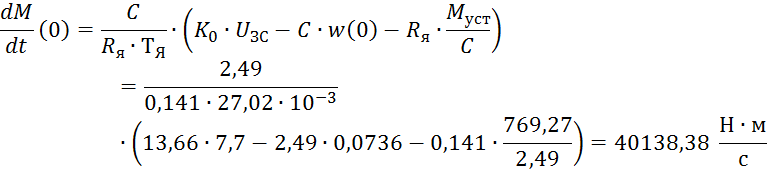
Характеристическое уравнение имеет вид:

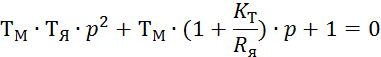
Найдём корни характеристического уравнения:

;

;

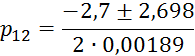
Т.к. корни характеристического уравнения вещественные отрицательные, то решение дифферинциального уравнения (4) и (5) будет иметь вид:

Найдём значение коэффициентов А,B,C,D, подставляя в полученные уравнения начальные условия для t=0.

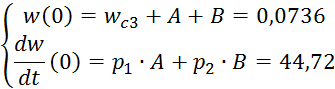
Решая данную систему получим:

Решая данную систему получим:

;

Окончательно получим:

Графическим способом определяем время переходного процесса 3-ого этапа:

Также определяем начальную скорость для 3-го этапа:

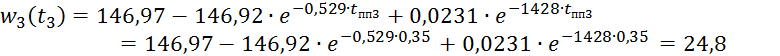
4 этап

;

Дифферинциальные уравнения относительно скорости и момента составленные по системе уравнений (*) имеют вид:

- по скорости

-по моменту

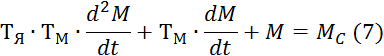
Найдём начальные условия:

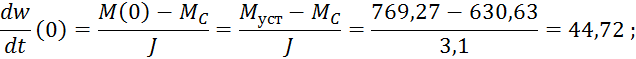
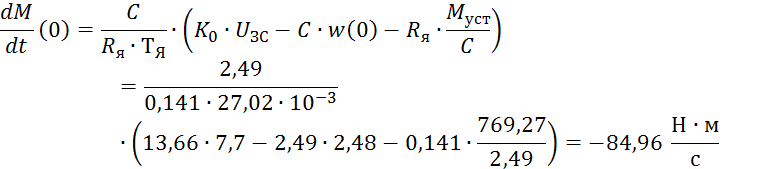
Характеристическое уравнение имеет вид:

Найдём корни характеристического уравнения:

Т.к. дискременант отрицательный , то корни характеристического уравнения будут комплексные.

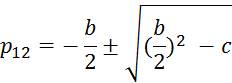
Где ,

Т.к. корни характеристического уравнения комплексные, то решение дифферинциального уравнения (2) и (3) будет иметь вид:

Найдём значение коэффициентов А,B,C,D, подставляя в полученные уравнения начальные условия для t=0.

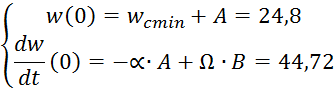
Решая данную систему получим:

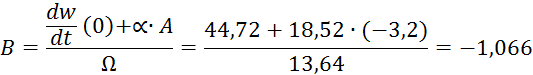
Решая данную систему получим:

;

Окончательно получим:

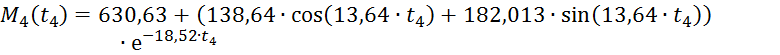
Остальные переходные процессы за цикл работы строим в системе Matlab Simulink.

Модель электропривода приведена на рис. 8.

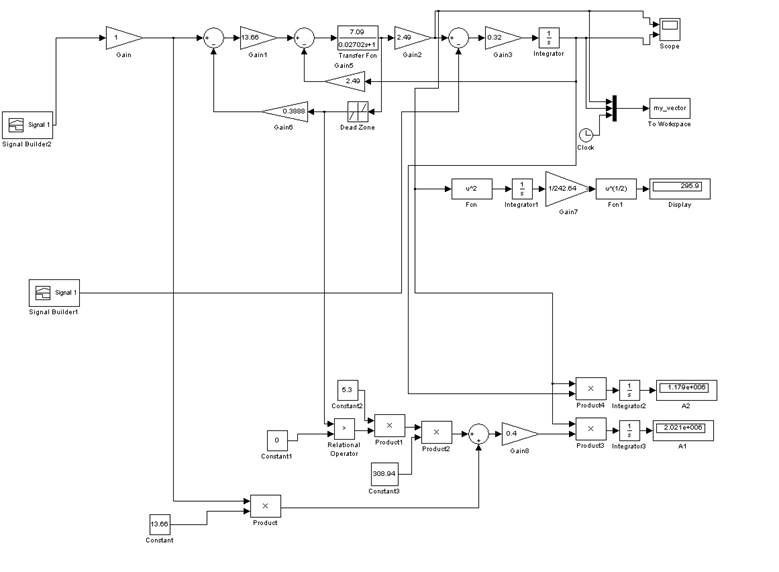
Рис. 8. Модель для расчета переходных процессов за цикл работы.

 

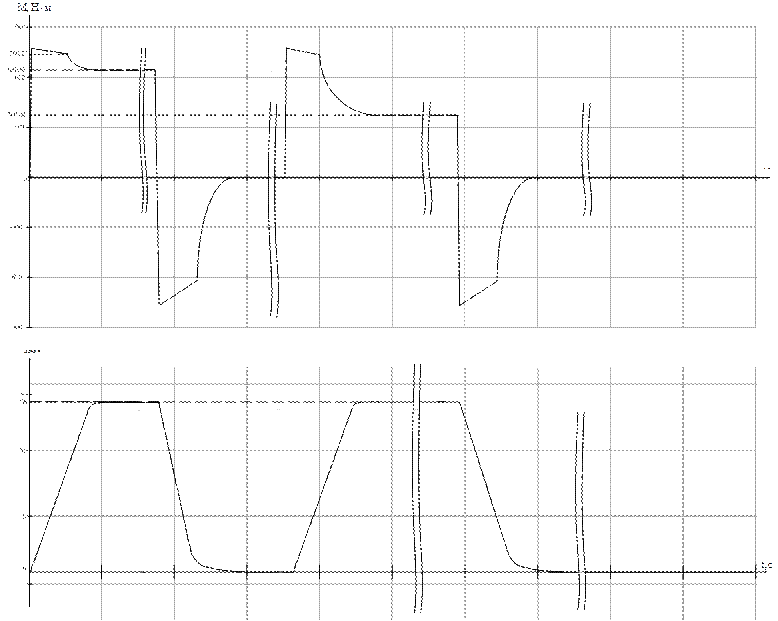
Рис. 9. Переходные процессы момента и скорости за цикл работы.

9. Окончательная проверка ЭД

Проверку двигателя по нагреву проведем с использованием метода эквивалентных величин.

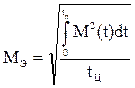
Рассчитаем эквивалентный момент в Matlab Simulink следующим образом (см. рис. 10).

Рис. 10. Фрагмент модели электропривода в Matlab Simulink реализующий расчет эквивалентного момента.

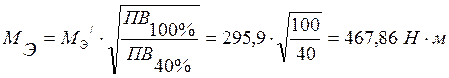
Т.к. эквивалентный момент меньше номинального

, то двигатель проходит по нагреву.

10. Расчет энергетики ЭП

КПД электропривода можно рассчитать следующим образом

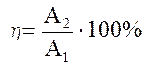, где  - энергия, потребляемая ЭП за цикл работы;

 - энергия, выделяемая ЭП за цикл работы.

Значения  и  найдем в Matlab Simulink (см. рис. 11).

 

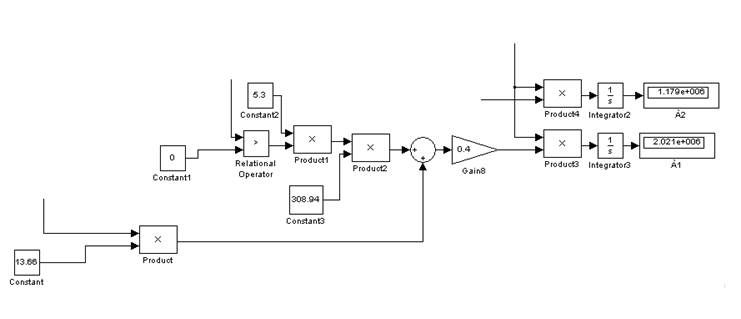
Рис.11. Фрагмент модели ЭП в Matlab Simulink реализующий расчет энергетики привода.

В блоке Relational Operator происходит сравнение сигнала ОС по току с нулем и если сигнал ОС по току становиться больше нуля (включена ОС по току), то на выходе Relational Operator появляется значение «1», в противном случае – «0». Т.о. получаем зависимость . И после блока Product2 имеем .

На вход блока Product3 подается сигнал .

В итоге на вход блока Product4 подается значение скорости идеального холостого хода  и текущего момента .

Блок Product перемножает значение текущей скорости  и текущего момента .

После интегрирования имеем значение потребляемой и выделяемой энергии.

Т.о. КПД электропривода составит