1. Представление форм булевых функций с использованием основных законов булевой алгебры
Необходимо отметить, что реализация конкретного устройства осуществляется в несколько этапов, а именно:
|
|
|
Рис. 1. |
2.1 Представление заданной БФ с помощью:
a) номеров наборов;
b) таблиц истинности;
c) СДНФ, СКНФ;
d) диаграммы Вейча-Карно.
Задача 1.
Представить булеву функцию трех аргументов f(x1,x2,x3) равную единице на наборах 0, 2, 3, 4, 6 и нулю на остальных наборах, в виде:
a) номеров наборов;
b) таблицы истинности;
c) СДНФ, СКНФ;
d) диаграммы Вейча-Карно.
Решение.
a) f0(X1,X2,X3) = 1,5,7 и f1 (X1,X2,X3) = 0,2,3,4,6
b) таблица истинности:
|
Таблица 1 |
|||||||||||||||||||||||||||||||||||||||||||||
|
c) СКНФ: f0(X1,X2,X3) = ![]() СДНФ:
СДНФ:
d) f1(X1,X2,X3) = ![]()
e) Диаграмма Вейча-Карно для булевой функции f(x1,x2,x3)
|
|
|
Рис. 1. |
2. Минимизация форм представления булевых функций и их реализация в различных системах логических элементов
2.1. Минимизация заданной БФ методом диаграмм Вейча-Карно:
Задача2.
Получить МДНФ и МКНФ булевой функции трех аргументов f(x1,x2,x3) равную единице на наборах 0, 2, 3, 4, 6 и нулю на остальных наборах.
Решение.
Наборы в двоичном алфавите имеют вид 000, 010, 011, 100, 110.
Строим диаграмму Вейча-Карно. Строим контуры (1, 2), получаем МДНФ:
f1(X1,X2,X3) = 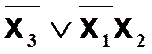
|
|
|
Рис.2. Диаграмма для булевой функции f(x1,x2,x3) |
Аналогично
для МКНФ: f0(X1,X2,X3) =
![]()
Задача 3
Имеем техническое устройство, 4-х точках которого установлены термодатчики Х1, Х2, Х3, Х4, фиксирующие превышение температуры над установленными значениями. Нарушение функционирования устройства возможно при одновременном перегреве точек:
Невозможными являются две ситуации: номера наборов 3 и 14.
Решение.
1. Составляем таблицу истинности.
|
Таблица 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. Строим диаграмму Вейча-Карно.
|
|
|
Рис.3. |
3. Получаем функцию
![]()
4. Строим устройство
|
|
|
Рис.4. |
2.2. Структурная реализация минимизированной БФ в булевом базисе элементов и в базисах элементов И-НЕ, ИЛИ-НЕ и выбор оптимального варианта.
Задача 4.
Построить структурную схему узла, реализующего функции
f1(X1,X2,X3) =![]() и f0(X1,X2,X3) =
и f0(X1,X2,X3) = ![]()
в булевом базисе элементов и в базисах элементов И-НЕ, ИЛИ-НЕ и выбрать оптимальный вариант.
Прежде чем приступить к решению данной задачи преподаватель должен напомнить обучаемым о функционально полных системах булевых функций, а также порядок синтеза комбинационных схем в базисе элементов И-НЕ и ИЛИ-НЕ:
Понятие о функционально-полной системе булевых функций
Каждой переключательной функции можно поставить в соответствие устройство – логический элемент. Набор ЛЭ, реализующий любую булеву функцию, называется функционально полным или базисом. Булев базис представляет собой операции НЕ, И, ИЛИ. При построении схемы логические операции заменяются соответствующими элементами. Существуют и другие функционально полные наборы ЛЭ. При помощи только элементов И-НЕ, а также только элементов ИЛИ-НЕ можно реализовать любую переключательную функцию. Поэтому они являются функционально полными и называются соответственно базис Шеффера и базис Пирса. Выбор этих базисов объясняется тем, что технология производства этих элементов является простой, надежной и дешевой. ЛЭ И-НЕ создаются по технологиям ТТЛ и МОП, а ИЛИ-НЕ по технологиям ЭСЛ и И2Л.
Для доказательства функциональной полноты базисов И-НЕ, ИЛИ-НЕ необходимо и достаточно реализовать в этих базисах операции инверсии, конъюнкции и дизъюнкции:
|
|
|
Рис.5. |
Порядок синтеза комбинационных схем в базисе элементов
И-НЕ и ИЛИ-НЕ:
Главной задачей при этом является избавление в записи МНФ от конъюнкций и дизъюнкций соответственно.
Построить схемы в выбранных базисах.
Решение.
|
|
|
Рис.6. |
|
|
|
Рис.7. |
Задача 5.
Синтезировать структурную схему узла реализующего заданную функцию:
|
Таблица 3 |
||||||
|
Решение.
Наборы в двоичном алфавите имеют вид 0000, 0001, 0110, 0111, 1000, 1001.
Строим диаграмму Вейча-Карно. Строим контуры (1, 2), получаем МДНФ:
f1(X1,X2,X3,Х4) = ![]()
|
|
|
Рис. 8. |
Структурная реализация минимизированной БФ в базисе Шеффера (элементов И-НЕ)
|
|
|
Рис. 9. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.