Математические модели оптимизации показателей качества

Раздел 2. Математические модели оптимизации показателей качества.

Графоаналитическое решение задач нелинейного программирования.

2.1 Безусловная оптимизация показателей качества с использованием целевой функции одной переменной.

Задачи, приводящиеся к одномерной оптимизации показателей качества.

          К задачам оптимизации целевой функции одной переменной приводятся наиболее простые модели безусловной оптимизации и некоторые задачи с ограничениями. Решение этих задач заключается в нахождении экстремума функции одной переменной.

Условия экстремума функции одной переменной. Рассмотрим задачу минимизации функции одной переменной на множестве вещественных чисел:

min f(x)                                      (2.1)

                                      x € X                                        (2.2)

Определение 1. Точка х^* представляет глобальный минимум функции f(x) на множестве Х, если х^* € Х и

f(х^*) ≤ f(x)                                 (2.3)

для всех   x € X.

Определение 2. Точка х^* называется точкой строгого глобального минимума функции f(x) на множестве Х, если х^* € Х и

f(х^*) < f(x)                                (2.4)

для всех   x € X, х ≠ х^*

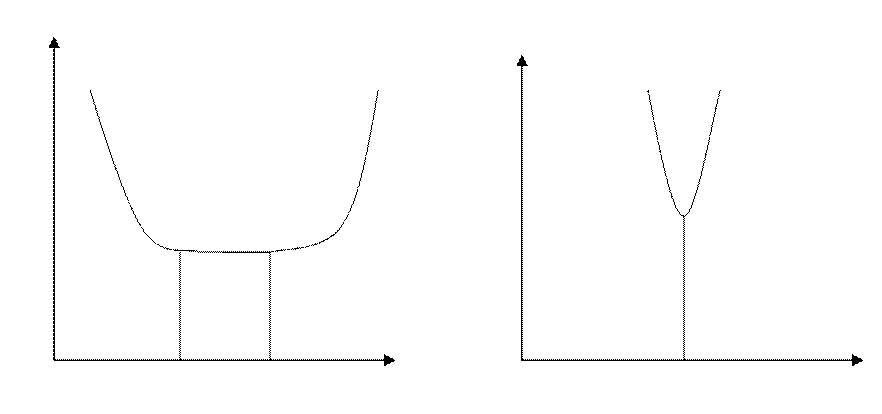
Рис.2.1 Строгий и нестрогий минимум.

        Определение 3. Точка х^* представляет локальный минимум функции f(x) на множестве Х, если при некотором достаточно малом έ > 0 для всех х ≠ х^*, х € Х, удовлетворяющих условию

│х -  х^*│≤ έ

выполнено неравенство

                             f(х^*) ≤ f(x)                           (2.5)

Определение 4. Если неравенство (5) – строгое, то точка х^* является точкой строгого локального минимума функции f(x).

Глобальный минимум одновременно является и локальным, но не наоборот.

          Все определения для максимума функции  получаются заменой       в выражениях (2.3), (2.4), (2.5) знака неравенства на обратный.

Теорема 1. Непрерывная функция f(x) достигает на замкнутом ограниченном множестве Х своего минимума ( во внутренней или граничной точке). (теорема Вейерштрасса).

Необходимое условие первого порядка. Рассмотрим условия, которые должны выполняться в точках локального экстремума функции, когда множество Х представляет вещественную ось. Предполагается, что f(x) имеет в окрестности х^* непрерывные производные до второго порядка включительно.

Теорема 2. Для того, чтобы функция f(x), определенная на вещественной оси, имела безусловный локальный экстремум в точке х^*, необходимо, чтобы в выполнялось условие

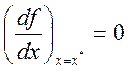                       (2.6)

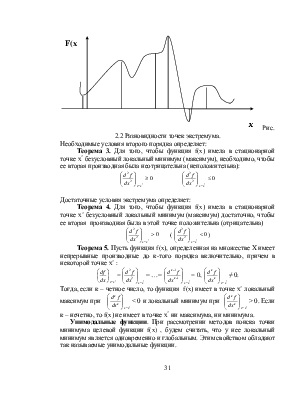
Условие (6) выделяет стационарные точки, но не определяет их характера. Это может быть максимум, минимум, точка перегиба.Рис. 2.2 Разновидности точек экстремума.

Необходимые условия второго порядка определяет:

Теорема 3. Для того, чтобы функция f(x) имела в стационарной точке х^* безусловный локальный минимум (максимум), необходимо, чтобы ее вторая производная была неотрицательна (неположительна):

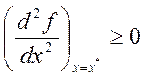
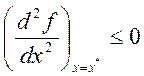
Достаточные условия экстремума определяет:

Теорема 4. Для того, чтобы функция f(x) имела в стационарной точке х^* безусловный локальный минимум (максимум) достаточно, чтобы ее вторая  производная была в этой точке положительна (отрицательна)

      ( )

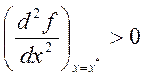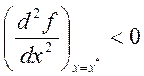Теорема 5. Пусть функция f(x), определенная на множестве Х имеет непрерывные производные до к-того порядка включительно, причем в некоторой точке х^* :

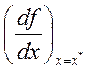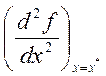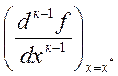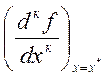== …= = 0, ≠ 0.

Тогда, если к – четное число, то функция  f(x) имеет в точке х^* локальный максимум при 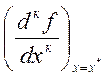  < 0 и локальный минимум при 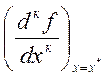 > 0. Если к – нечетно, то f(x) не имеет в точке х^* ни максимума, ни минимума.

Унимодальные функции. При рассмотрении методов поиска точки минимума целевой функции f(x) , будем считать, что у нее локальный минимум является одновременно и глобальным. Этим свойством обладают так называемые унимодальные функции.

Определение. Функция называется унимодальной на отрезке [ a,b], если она непрерывна на этом отрезке и существуют числа α и β (а≤α≤β≤b), такие, что:

1)  если а<α, то на отрезке [ a,α ]  функция f(x) монотонно убывает;

2)  если β<b, то на отрезке  [ β,b ] функция f(x) монотонно возрастает;

если  х є [ α, β ], то f(x) = f^*(x)  =  min  f(x).

                                                  x є[ a,b  ]

Таким образом, функция f(x) является унимодальной на отрезке [ a,b ], если у нее существует единственная точка минимума х^* є [ a,b ], причем f(x) cтрого убывает при х є [ a,x^*) и строго возрастает при  х є ( x^* ,b ].

          Для применения методов оптимизации, использующих производные функции f(x) необходимо, чтобы функция была выпуклой на [ a,b ]. Рассмотрим некоторые свойства выпуклых функций.

          Определение. Функция f(x), заданная на отрезке [ a,b ] называется выпуклой на этом отрезке, если для всех х^΄, x΄΄ є [ a,b ] и произвольного числа α є [ 0,1 ] выполняется неравенство:

                       F[ α х^΄+(1-α) x΄΄] ≤ α f(х^΄) + (1 – α) f(x΄΄)

Основные свойства выпуклых функций:

1.  Если функция f(x) выпукла на [a,b], то на любом отрезке [x^′, x^″]є [a,b] ее график расположен не выше хорды, проведенной через точки графика с абсциссами x^′ и x^″.

2.  Условия выпуклости могут быть представлены в виде:

а) для того, чтобы дифференцируемая на отрезке [a,b] функция f(x) была выпуклой на этом отрезке, необходимо и достаточно,  чтобы производная f^′(x) не убывала на [a,b.

б) для того, чтобы  дважды дифференцируема на отрезке [a,b] функция f(x), была выпуклой на этом отрезке необходимо и достаточно, чтобы при всех xє [a,b] выполнялось неравенство f^″(x)>0

3.  Условие выпуклости для дифференцируемой на отрезке [a,b] функции f(x) означает, что на этом отрезке любая касательная к графику f(x) лежит не выше этого графика.

4.  Если f(x) – выпуклая дифференцируемая на [a,b] функция и в точке x*є[a,b] выполняется равенство f^′(x*)=0,то x* является точкой глобального минимума f(x) на [a,b].

5.  Всякая выпуклая непрерывная на отрезке [a,b] функция является и унимодальной на этом отрезке.

     Прямые методы. Прямые методы нахождения экстремума целевой функции – это методы, использующие только значения функции и не требующие вычисления производных. Прямые методы являются приближенными и позволяют найти решение с нужной точностью в результате определения конечного числа значений функции f(x) в некоторых точках [a,b].

Достоинством прямых методов является отсутствие ограничений непрерывности и дифференцируемости целевой функции. Кроме того целевая функция может быть не заданна в аналитическом виде, т.к. прямые методы основаны на возможности определения значений целевой функции в заданных точках.