Метод парабол. В методе парабол, кроме сравнения значений в двух точках, как это имеет место в методе исключения отрезков, используется информация, содержащаяся в относительных изменениях значений f(x) в пробных точках. Метод парабол является простейшим из методов полиномиальной аппроксимации, которые основаны на том, что функция f(x) апроксимируется многочленом. Точка минимума этого многочлена является приближенным значением точки x* минимума функции f(x). При этом на функцию f(x) накладываются ограничения унимодальности и гладкости. На каждой итерации метода парабол строится квадратный трехчлен, график которого представляет параболу и проходит через три выбранные точки графика функции f(x).
Пусть функция f(x) является унимодальной на отрезке [a,b] и достигает минимума во внутренней точке отрезка. На отрезке [a,b] выбираем три точки x1, x2, x3, для которых выполняются неравенства:
x1<x2<x3; f(x1) ≥ f(x2) ≤ f(x3) (2.10)
Т.к. функция унимодальна, то x*є[x1,x3].
Рассмотрим квадратный трехчлен в виде q(x)=a0+a1(x-x1)+a2(x-x1)(x-x2). его график проходит через точки (x1,f(x1)); (x2,f(x2)); (x3,f(x3))графика функции f(x). из (2.10) следует, что ветви искомой параболы направлены вверх, а точки минимума принадлежат отрезку [x1,x3].
Коэффициенты a0,a1,a2 можно найти из системы уравнений:
q(x1)=f1(x1); q(x2)=f2(x2); q(x3)=f3(x3)
Решая систему найдем:
a0=f1; a1 = (f2 – f1) ( x2-x1)-1; a2 = ( x3 –x2)-1 [(f3 -f1) (x3 -x1 )-1 – (f2-f1) (x2-x1)-1]
Точка
минимума квадратного x трехчлена q(x) можно найти из условия равенства нулю производной q′(x): x
=1/2(x1+x2-a1/a2),
Число x является очередным приближением к точке минимума функции x*.
Затем данная
процедура выполняется для новых точек x1, x2, x3, которые
удовлетворяют неравенствам (2.10). Причем выбрать эти точки можно используя
метод исключения отрезков при переходе от исходного отрезка к новому [x1,x3]
содержащему точку x*. В качестве пробных точек используются
точки x2 и x, в
которых сравниваются значения функции f(x). В этом случаи начало и конец нового отрезка, и пробная
точка образуют тройку чисел, удовлетворяющую (2.10). На каждой итерации необходимо
одно новое значение функции f(x).
Условием окончания является условие:
│∆│≤ ε,
где ε - заданная
точность определения точки x*, ∆ -
разность чисел x, найденных на данной и
предыдущей итерациях. Точность метода парабол выше чем точность метода
исключения отрезков, при одном и том же количестве вычислений.
Методы, использующие производные функции. Прямые методы используются при минимальных требованиях к функции, когда необходимо выполнение требования унимодальности, а вычисление производных не выполняется. Эффективность методов возрастает, если к функции предъявить требования дважды дифференцируемости и выпуклости, и вычислять производные в пробных точках.
Метод средней точки – заключается в том, что в средней точке xc=(a+b)/2 отрезка вычисляется значение производной f′( xc).
Если f′(x)>0, то точка xc лежит на участке монотонного возрастания функции f(x) и, следовательно, x*< xc
, а точка минимума находится на отрезке [a, x]. Если же f′( xc) < 0, то точка xc лежит на участке убывания функции f(x) и x*є[x, b]. При f′( xc)=0 точка минимума x*= xc.
В случае метода средней точки на каждой итерации вычисляется только одно значение f′(x). Отрезок поиска при этом уменьшается вдвое. Если │f′(x)│< ε на очередной итерации, то поиск заканчивается и следует положить x* ≈ xc и f* ≈ f(xc).
Метод хорд. Для выпуклой дифференцируемой функции f(x), если производная на концах отрезков [a,b] имеет разные значки (f′(a) f′(b)<0) задача нахождения минимума f(x) эквивалентна решению уравнения.
f′(x)=0, xє(a,b).
Метод хорд основан на исключении отрезков путем определения точки x^ пересечения хорды графика функции f′(x) с осью 0x. на очередном отрезке
x^= a - f′(a) (a – b)/ [f′(a) - f′ (b)] (2.11)
Отрезок дальнейшего поиска точки x*([a,x^] или (x^,b]) выбирается в
 |
f(x)
 |
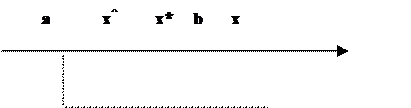Рис. 2.3. Исключение отрезков в методе хорд.
зависимости от знака также как в методе средней точки. На каждой итерации кроме первой следует вычислять одно новое значение f′(x). Поиск заканчивается при выполнении условия │ f′(x^)< ε, полагая x*≈ xc, f*≈f(xc).
Метод Ньютона (метод касательных) заключается в том, что для дважды дифференцируемой, выпуклой (f″(x)>0) функции корень уравнения f′(x)=0 находится методом касательных. Метод состоит в построении последовательных приближений xk, k=0,1…, на основе применения аппроксимирующей функции в виде касательной к графику функции f′(x). Точка, в которой линейная аппроксимирующая функция обращается в ноль, используется в качестве следующего приближения xk+1. Уравнение касательной к графику функции f′(x) имеет вид: y= f′(xk)+ f′′(xk) (x-xk)
Из условия найдем y=0 точку xk+1:
xk+1=xk - f′(xk)/ f′′(xk
Выбирая в качестве начального приближения точку x0 получим при k=0,1… последовательность точек xk. Вычисления проводят до тех пор, пока не выполниться условие │ f′(xk)│≤ ε. Затем полагают x*≈xk, f*≈f(xk). При x0 достаточно близком к x* метод обеспечивает высокую скорость сходимости.
Метод кубической аппроксимации. В этом методе функция аппроксимируется многочленом третей степени. Считая, что f(x) является выпуклой дифференцируемой функцией, которая в интервале (x1,x2) содержит точку минимума x*, аппроксимирующий полином представим в виде:
q(x)=a0=a1(x-x1)+a2(x-x1)(x-x2)+a3(x-x1)2(x-x2),
где x1 и x2 точки, в которых совпадают значения функции f(x) и значения q(x), а также значения их производных. Из условия q(x1)=f(x1); q(x2)=f(x2); q′(x1)=f′(x1); q′(x2)= f′(x2) получаем систему алгебраических уравнений для определения коэффициента: a0=f(x1); a0+a1(x2-x1)=f(x2); a1+a2(x-x2)= f′(x1); a1+a2(x2-x1)+a3(x2-x1)= f′(x2).
Из условия f′(x)=0 получим квадратное уравнение для определения значения x0, принадлежащего интервалу (x1,x2). Этот корень является точкой минимума полинома q(x) и является приближением к точке минимума функции f(x). В качестве новой пары точек x1, x2 для следующей итерации выбираются концы одного из отрезков [a, x0] и [x0,b], которые содержат точку x*. Выбор того или иного отрезка осуществляется в зависимости от знака производной f′(x0), как в методе средней точки. Поиск заканчивается при выполнении неравенства │f′(x0)│≤ 0. При этом полагают, что x* ≈ x0, f* ≈ f(x0).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.