Следовательно, если провести касательную в любой точке годографа, то по наклону касательной можно определить скорость v(z) на некоторой глубине z которой достиг луч рефрагированной волны.
В случае если ниже преломляющей границы скорость vГ остается постоянной то луч рефрагированной волны падая на эту границ под критическим углом преломится и начнет вдоль преломляющей границы в подстилающей среде со скоростью vГ . Это волна в каждой точке которой она достигла, порождает другую преломленную волну – головную рефрагированную (лучи этой волны имеют криволинейную форму).
Годограф головной рефрагированной волны является отрезком прямой линии и описывается уравнением
x
t(x)= 
vГ +t0.
В силу горизонтальности преломляющей границы скорость распространения головной рефрагированной волны вдоль земной поверхности (кажущаяся скорость vK) – равна скорости vГ, с которой преломленная волна скользит вдоль преломляющей границы vК = vГ. Следовательно по наклону годографа головной рефрагированной волны можно определить vГ . При выполнении полевых наблюдений используется способ первых вступлений, при котором регистрируются вступления двух волн – прямой рефрагированной и головной рефрагированной.
Интерпретация годографов рефрагированных волн заключается в определении закона изменения скорости с глубиной и глубины залегания преломляющей границы. Для интерпретации используется эмпирический способ Кондратьева. Суть данного способа сводится к тому что, на годографе прямой рефрагированной волны выбирается несколько (до 5) точек t1, t2,,… с абсциссами х1, х2, … в каждой из которых проводится касательная, по пересечению касательных с осью времени t определяется о t01, t02,,…, а по наклону касательных – кажущиеся скорости vК1, vК2,…, равные скоростям v(h) в градиентной среде на глубинах h1, h2, …hi. Для определения глубин H соответствующих точкам годографа t1, t2,,… с абсциссами х1, х2, … используется формула t0:
t0v(h)
H =
v(h) 2 ,,,
2 1−( )
v(h)
где
v(h) - средняя скорость в
среде от земной поверхности до глубины
H
v(h) = 12⎛⎜⎜⎝ xtii +
xtii v(h)⎞⎟⎟⎠.
Для определения глубины залегания преломляющей границы достаточно определить глубину h для последней точки годографа прямой рефрагированной волны (точка соответствует выходу волне коснувшейся преломляющей границы).
Упругие свойства горных пород характеризуются упругими постоянными: 1) модулем Юнга Е, который представляет собой коэффициент пропорциональности между приложенной силой на единицу площади Fs и возникшей деформацией, т. е. Fs = Еε и характеризует сопротивление горной породы растяжению или сжатию; 2) коэффициентом Пуассона μ, который определяется как отношение поперечной деформации к продольной, т.е. μ =εw/εl; 3)скоростью распространения продольныхvPипоперечных vS волн.
Упругие параметры пород можно измерить двумя методами: статическими и динамическими. Статический метод основан на измерении деформаций и статических напряжений. Динамический метод основан на изучении распространения упругих волн в исследуемых веществах.
Измерение скоростей сейсмических волн на образцах может быть выполнено по методике профилирования или по методике просвечивания.
Сущность методики профилирования (Рис. 14) сводится к следующему; на подготовленном к исследованиям образце размечается линия наблюдений и вдоль нее через постоянный интервал (1-2см) наносят метки. При измерениях излучатель располагается неподвижно на одном конце линии наблюдений, а приемник последовательно перемещается в каждую из размеченных точек.
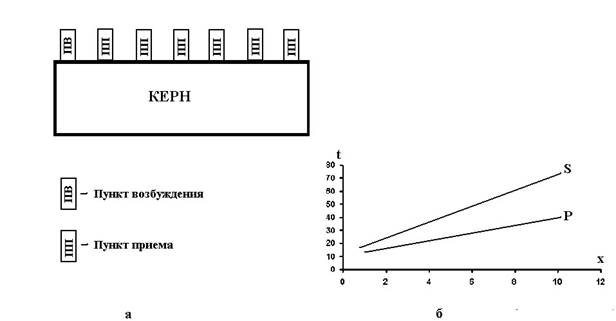
Рисунок 54 Ультразвуковое профилирование: а – схема работ, б – годографы сейсмических волн P и S
Определяются, времена первых вступлений упругих волн и по ним строится годограф. Для однородной среды уравнение годографа имеет вид x
линейной зависимости t(x) = 
.
График этой зависимости является пряv
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.