Изучение геологического строения массивов горных пород. Расчленение горизонтально-слоистых сред. Изучение подземных вод в массивах горных пород, страница 20

2  По круговой диаграмме по направлению максимального смещения изолиний определить направление движения потока подземных вод.

3  На миллиметровке построить график смещения эквипотенциальных линий в направлении потока за время измерений.

4  По графику определить скорость движения потока.

5  Оформить результаты в виде пояснительной записки с приложением графических материалов. 

Лабораторная работа 2 

«Определение скорости фильтрации подземных вод по данным резистивиметрии»

Цель работы: определение скорости фильтрации подземных вод скважинным резистивиметрическим методом.

Материалы и оборудование: миллиметровая бумага, калькулятор.

Задание

Определить скорость фильтрации подземных по данным резистивиметрических исследований в гидрогеологической скважине (данные выдаются преподавателем) 

Ход работы

1  По данным полевых резистивиметрических измерений в скважине исследований построить резистивиметрические кривые. Построения выполнять на миллиметровке.

2  Проанализировать резистивиметрические кривые и сделать выводы о поведении подземного потока.

3  На заданной глубине по ризистивимитрическим кривым определить величину удельного сопротивления подземных вод.

4  По номограмме (приложение 1) пересчитать значения удельного сопротивления вод в величину минерализации.

5  Построить график зависимости  С_п-С₀ от времени и найти угловой коэффициент tgα. 

6  По соответствующей формуле определить скорость фильтрации подземного потока.

7  Результаты оформить в виде пояснительной записки с приложением графических материалов.

 

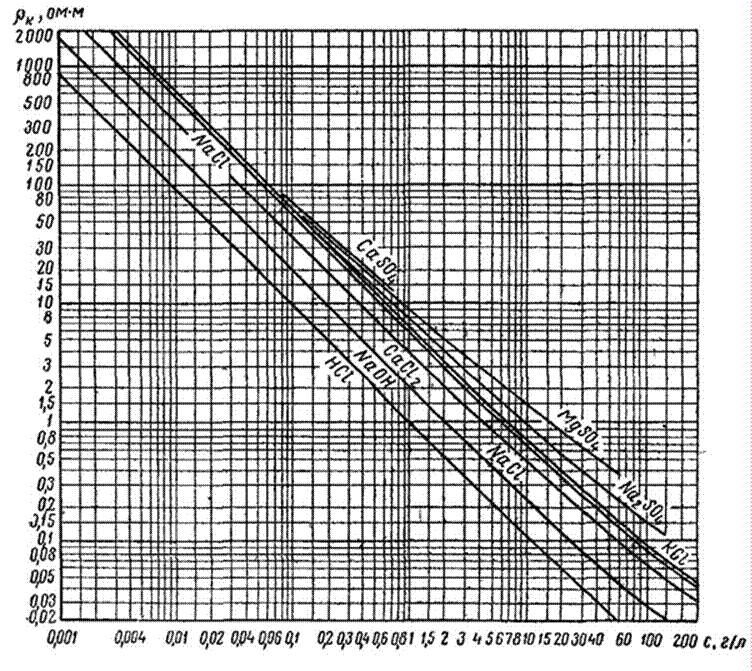
Приложение 1 Номограмма для определения минерализации подземных вод 

Тема 4 Изучение свойств и характеристик горных пород  

1  Понятие о градиентной среде.

2  Сейсмический метод исследования градиентныхсред.

3  Упругие свойства горных пород.

4  Методика лабораторного определения упругих свойств пород.

Основные понятия по теме

При решении задач инженерной геологии огромное значение имеет изучение зоны выветривания скальных пород, неконсолидированных терригенных отложений, не полностью промерзших горных пород и других геологических сред, в которых скорость плавно увеличивается с глубиной. Такого рода среды называются непрерывными или градиентными, поскольку особенности распространения упругих волн в них определяется величиной и направлением градиента скорости, который направлен по нормали  к изолиниям равных скоростей.

Наибольшее    практическое        применение          нашла           вертикальнонеоднородная модель среды, для которой скорость является только функцией глубины v =v(z). Во многих случаях изменение скорости с глубиной с достаточной точностью описывается линейным уравнением v(z) = v₀(1+γz) _,

где γ - относительный вертикальный градиент в м^-1 или км^-1. Для зоны интенсивного выветривания γ=50÷150 м^-1, для терригенных пород - γ=10÷50 м^-1, для кристаллических метаморфизованных отложений γ=0,5÷5 м^-1.

Сейсмические волны, распространяющиеся в градиентных средах, называют прямыми рефрагированными волнами (рис. 13). Для них характерна криволинейная форма лучей. Если закон изменения скорости с глубиной, v(z) = v₀(1+βz) то уравнение годографа прямой рефрагированной волны имеет вид:

                                                                                             2            xγ

t(x)=γv arcsh 2 0

где arcsh – арксинус гиперболический (arcshα= ln(α+ α² +1) ).  Для других законов изменения скорости уравнение годографа будет иметь более сложный вид. В соответствии с законом преломления Согласно уравнению

v(z)

= const , sinβ(z)

луч, выходящий в точку на земной поверхности не может проникнуть на глубину больше некоторой предельной глубины z_m, на которой угол преломления будет равен 90°

 

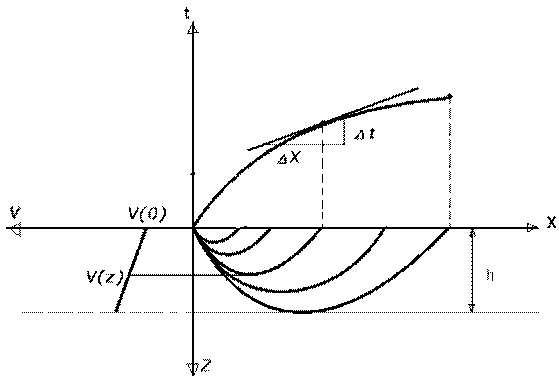
Рисунок 13Лучи и годограф прямой рефрагированной 

й

v(z_m) = v(0) = v_K , т.к. sinβ(z_m) = sin90_o =1, то

                       sinβ(z_m)      sinβ(0)

v(zm) =vK .

Так как в градиентной среде скорость с глубиной возрастает, то на земной поверхности  можно наблюдать волны, которые достигли различной глубины в среде и которые называются прямыми рефрагированными.