Математика \ Вычислительная математика

Способы решения линейных дифференциальных уравнений (ЛДУ), страница 3

    k3=y;

    p=[t,y'];

    out(i,:)=p;

    f1=f2;f2=f3;

    f3=mf(t,y,a,f);

    t=t+h;

end %A-B method end

%Plotting

x=(out(:,1))';

z=(out(:,2))';

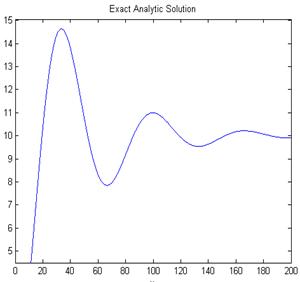
s1=10.-.123464044002483951e-2.*exp(-8.7869940561404014486.*x)-9.9987653595599751605.*exp(-.23169638596465942357e-1.*x).*cos(-.94587955120305269160e-1.*x)+2.5639264290192386911.*exp(-.23169638596465942357e-1.*x).*sin(-.94587955120305269160e-1.*x);

hold on

subplot(2,1,1);

plot(x,z);

subplot(2,1,2);

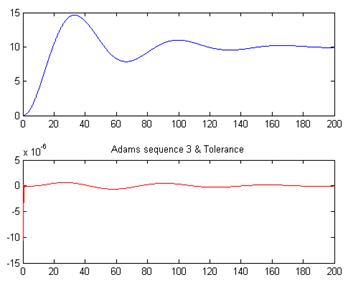
plot(x,s1-z,'r');

hold off

title('Prognoz korrekcii 3-ego poryadka i pogreshnost rezultatov')

%************%

%ODE45 solver%

%************%

figure;

y0=[0;0;0];

options=odeset('RelTol',2.22045e-014,'AbsTol',1e-15);

[T,Y]=ode45(@oscil,[0 200],y0,options);

x=T;

s1=10.-.123464044002483951e-2.*exp(-8.7869940561404014486.*x)-9.9987653595599751605.*exp(-.23169638596465942357e-1.*x).*cos(-.94587955120305269160e-1.*x)+2.5639264290192386911.*exp(-.23169638596465942357e-1.*x).*sin(-.94587955120305269160e-1.*x);

subplot(2,1,2);

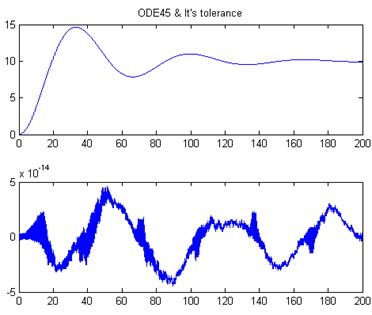
plot(x,Y(:,1)-s1);

subplot(2,1,1);

plot(T,Y(:,1));

title('ODE45 & It'' tolerance')

4. Графики:

5. Выводы:

h

Погрешность

0,001

1*10-11

0,01

1*10-8

0,05

1*10-6

0,1

1*10304
Скачать файл