Изучение свойств линейного нейрона и линейной нейронной сети, страница 4

\ \   адаптация с начальным вектором задержки pf

[net,   у,   е,  pf]   = adapt (net,  p2,   t2,  pf);

mse (e) ;

Адаптируем сеть на 100-разовом прогоне последователь­ности:

\\   формирование новой последовательности входов

р3  =   [Р1  p2];

\\   формирование новой последовательности выходов

t3 =   [T1   t2];

\\   установка  количества  проходов

net.adaptParam.passes  = 100;

\ \  адаптациянейрона

[net,  у,   е]  = adapt (net,  р3,   t3) ;

mse (e) ;

Получим приемлемую ошибку, значит сеть обучена зави­симости выходов от входов.

Пример 8. Изучение возможности линейного нейрона решать линейно несепарабельные задачи

Проведем эксперимент с линейным нейроном по класси­фикации пяти входных векторов на две категории, которые линейно несепарабелльны.

Определим входы ли­нейного нейрона:

\\   входы линейного нейрона

Р =   [-0.5  -0.5  +0.4   -0.1   -0.9;-0.5  +0.5  -0.5  +1.0  +0.0];

и вектор желаемых векторов:

Т =   [1   1   0  0  0];  выходы — реакции нейрона  на  входы Р

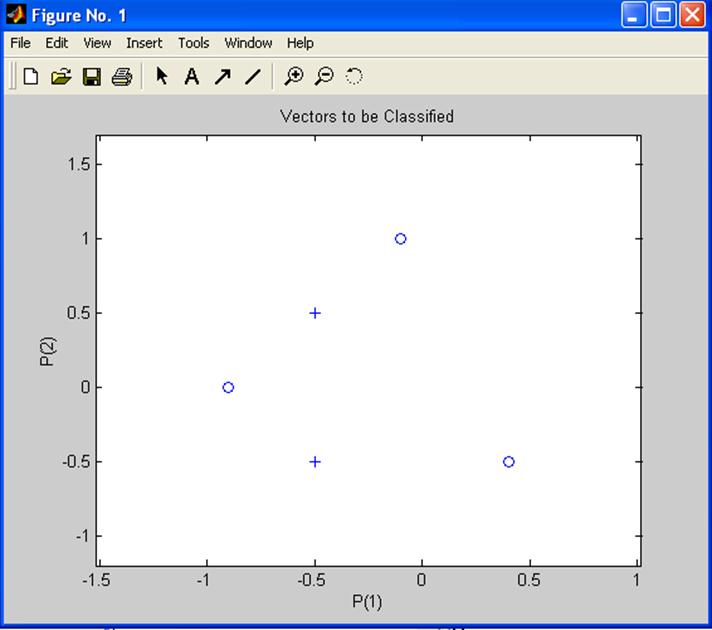
Поскольку векторы разных видов нельзя отделить прямой линией, их классификация невозможна.

\\ создание нейрона                                                                     

net = newp([-2 2; -2 2],1);

\\ изображение обучающей выборки                                        

plotpv(P,T) ;        

\\ изображение разделяющей прямой                                      

linehandle = plotpc (net. IW{1}, net.b{1});

Обучим нейрон классифицикации векторов.                          

\\ организация цикла обучения нейрона                              

for а = 1 : 20;

\\ адаптация нейрона

[net, Y, Е] = adapt (net, Р, T) ;

\\ получение управляющей структуры изображения

для новой разделяющей прямой

linehandle = plotpc (net. IW{1}, net.b{1}, linehandle);

\\ изображение разделяющей прямой

drawnow;

\\ конец цикла

end;

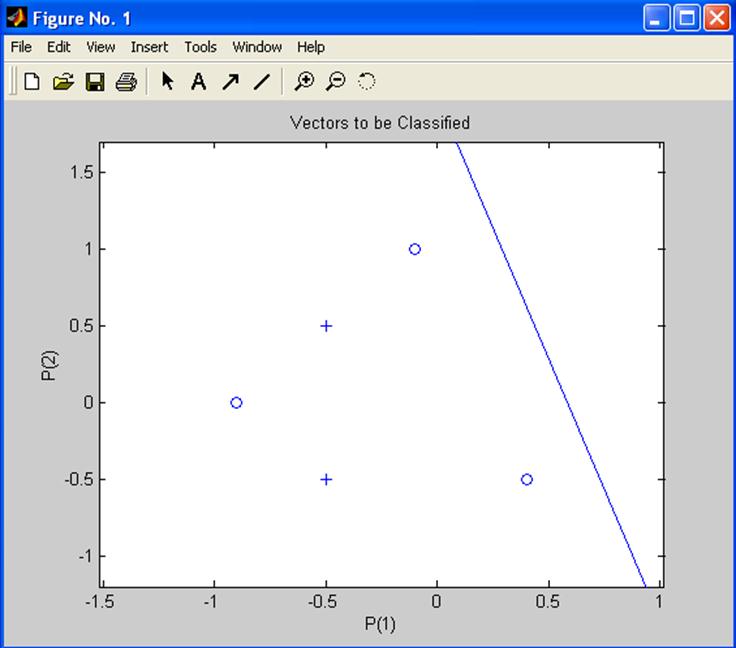
Цикл дает возможность адаптировать нейрон при одном проходе, изобразить линию классификации и остановиться

Нулевая ошибка, а следовательно, и классификация никогда не будет получена. Фундаментальное свойство линейного нейрона — ограничение линейно сепарабельными данными.

Пример 9. Процесс обучения линейного нейрона

Для выполнения примера будем использовать функции: newlin — для создания нейрона, train — для обучения, sim — для имитации поведения нейрона. Определим входы нейрона и желаемые выходы:

\\   определение входов нейрона

р =   [1.0  -1.4];

\\   определение выходов  нейрона

Т =   [0.5  1.0];

Вектор p задает два входных элемента. Используем линейный нейрон с одним входом для решения задачи. Установим интервалы изменения весов и порогов:

\\ установка интервала весов

w = -1 : 0.1 : 1;

\\ установка интервала пороговых значений

b = -1 : 0.1 : 1;

Вычислить и изобразить ошибку нейрона можно следую­щим образом:

\\   формирование поверхности ошибки в координатных

осях — весов и пороговых значений

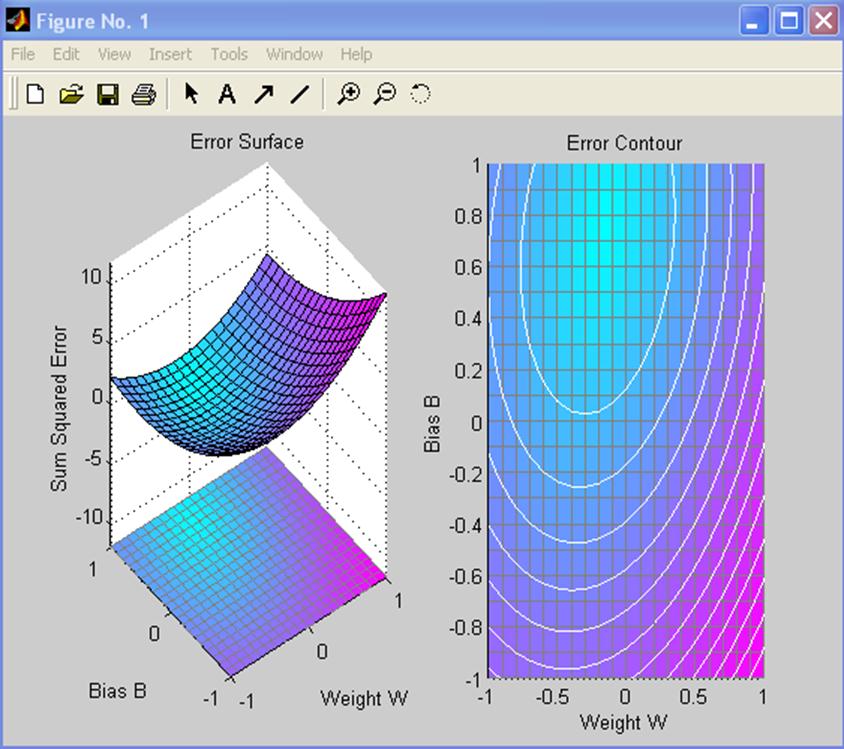
ES  =  errsurf (p,   T,   w,   b,    'purelin');

\\  изображение поверхности ошибки

plotes(w,   b,   ES) ;

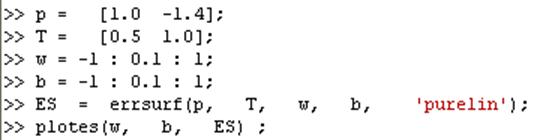
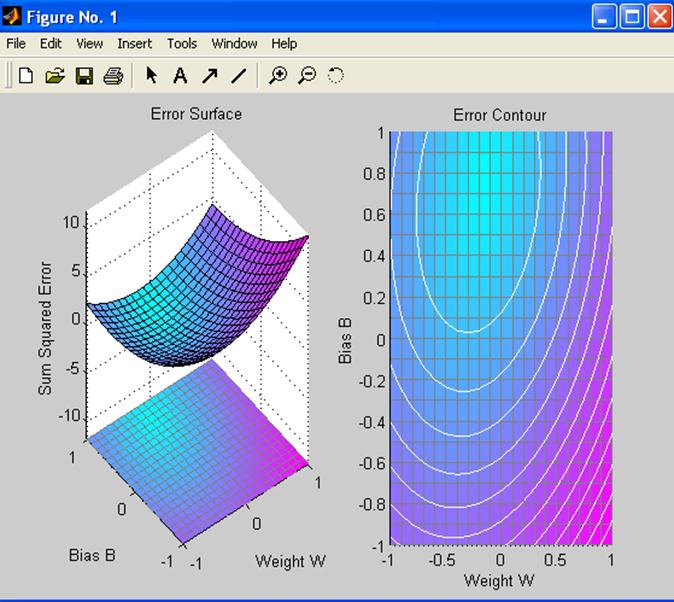
Лучший вес и значение порога — это самые низкие точки на поверхности ошибки. Переопределим уровень обученности и создадим нейрон.

\\   возвращение максимального уровня обученности

для линейного слоя с bias, для обучения на основе Р

maxlr =  0.20   * maxlinlr(p,    'bias');

net  = newlin([-2 2],1,[0],   maxlr);

Функция maxlinlr находит значение, соответствующее са­мому быстрому уровню обученности линейной нейронной сети. Возьмем 20 % от вычисленного уровня.

Функция newlin содержит четыре параметра:

•    матрицу интервалов входов размерностью R х 2;

•    количество элементов в выходном векторе;

•    вектор задержек входов;

•    уровень обучения.

Установим целевое значение ошибки:

\\ установка целевого значения ошибки

net.trainParam.goal = . 001;

Получим поверхность ошибки.

\\   формирование поверхности ошибки

ES = errsurf(P,   т,   w,  b,   'purelin');

\\  изображение поверхности ошибки

plotes (w,   b,   ES);

\\   создание 2 координатных осей в графическом окне

и установка первых осей активными

subplot (1,   2,   2);

Произвольно изменим веса нейрона в установленных интервалах:

net.IW{1, 1}=0;

\\  произвольное изменение весов нейрона

net.b{1}   =  0.1;

\\  эпоха  обучения нейрона,   формирование истории обучения  tr.

[net,   tr]  =  train (net,   p,   T) ;

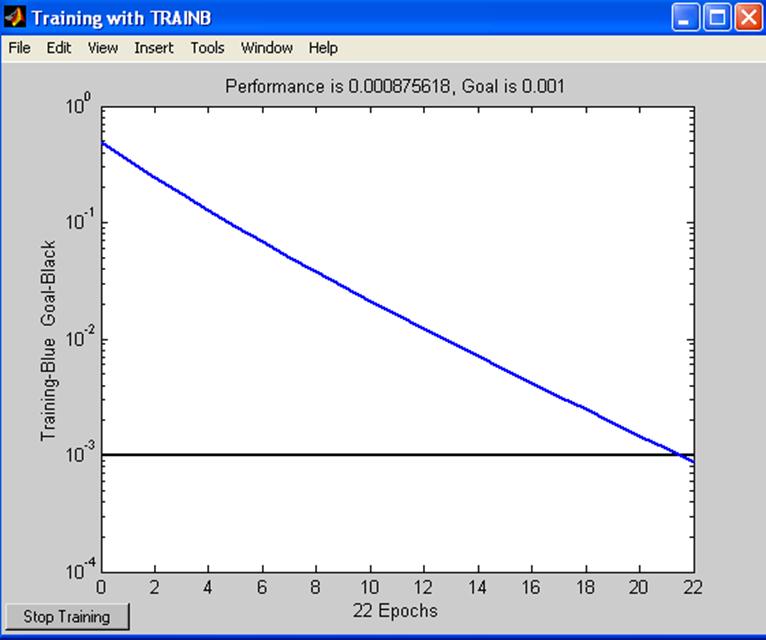
Функция train выводит на экран историю обучения обученной сети (tr). График  показывает падение ошибки в ходе обучения:

\\ изображение истории обучения на поверхности ошибки

plotperf(tr,  net.trainParam.goal);

P =  -1.1;

\\   формирование выхода  обученного нейрона для входа -1,1.

а  =  sim (net,  P);

Используем функцию sim, чтобы протестировать нейрон для входа -1.1 и посмотрим, будет ли выход равен 1, 0. Результат очень близок к 1.

Контрольные вопросы

1.  Какие функции выполняет линейный нейрон

2.  Какие функции активации используются в НС

3.  Какие задачи называют линейно сепарабельными

4.  Можно ли обучить линейный нейрон выполнять логическую функцию исключающее ИЛИ

5.  Какой алгоритм использует для обучения однослойные НС