Изучение свойств линейного нейрона и линейной нейронной сети, страница 3

Начнем с классификации векторов на основе двухвходового нейрона. Будем использовать функцию newp для созда­ния нейрона, sim для имитации его работы, adapt для адапта­ции (обучения) нейронной сети. Обучим двухвходовой ней­рон классифицировать входные векторы на две категории. Определим четыре входных вектора нейрона.

\\ определение четырех двухэлементных входов

Р = [ -0.5 -0.5 +0.4 -0.2; -0.5 +0.5 -0.4 +1.0];

Зададим желаемые выходы нейрона для определенных векторов.

Т= [1 1 0 0];

определение выходов нейрона — реакций на входы Р. Изобразим входные векторы (точки) на плос­кости:

plotpv (P, T)

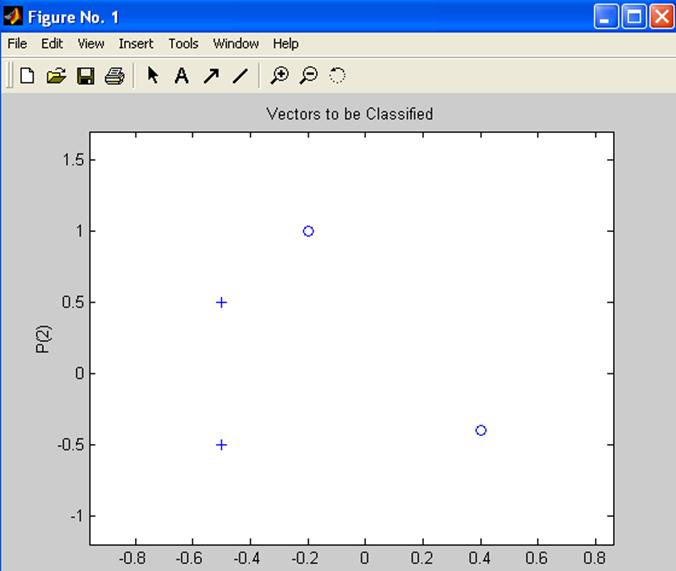
Каждый из четырех входных векторов на плоскости Р оп­ределяется двумя координатами, представленными как двух­элементные столбцы в матрице Р.

Создадим один линейный нейрон с двумя входами, зна­чения которых лежат в интервале [-1, 1].

\\   создание линейного нейрона  с двумя входами из интервала   [-1,   1]

net  = newp ([-1   1;   -1   1],   1);

Нейрон по умолчанию имеет функцию активации hardlim и такой нейрон разделяет входные векторы прямой линией.

Определим координаты линии классификации: веса (IW) и порог срабатывания нейрона (b).

\\  получение управляющей структуры linehandle

для изображения разделяющей линии в координатах весов   (IW) и порога   срабатывания нейрона (b) .

linehandle = plotpc (net. IW{1},   net.b{1}) ;

\\  изображение разделяющей прямой

plotpc (net. IW {1},   net.b{1});

Если исходным весам задать нулевые значения, то любые входы дадут одинаковые выходы, и линия классификации не будет видна на плоскости. Проведем обучение:

\\   очистка  координатных  осей

clf;

\\ изображение входных векторов двух категорий,

категория задается элементами вектора Т

plotpv(P, Т) ;

\\ получение управляющей структуры linehandle

linehandle = plotpc(net. IW {1}, net.b{1});

\\ присвоение начального значения ошибки

Е = 1;                                                                                                   

\\ инициализация нейрона                                                          

net = init (net) ;                                                                            

\\ получение управляющей структуры linehandle

linehandle = plotpc(net. IW{1}, net.b{1});       

\\ организация цикла пока ошибка не равна 0

while (mse (E));

\\ адаптация нейрона net на обучающей выборке <Р, Т>,

функция возвращает адаптированный нейрон net,

выход Y, ошибку Е

[net, Y, Е] = adapt (net, Р, Т) ;                                        

\\ изображение разделяющей прямой нейрона после   

адаптации                                                                                       

linehandle = plotpc(net. IW{1}, net.b{1}, linehandle);

\\ очистка окна графиков

drawnow;

\\ конец цикла while

end;

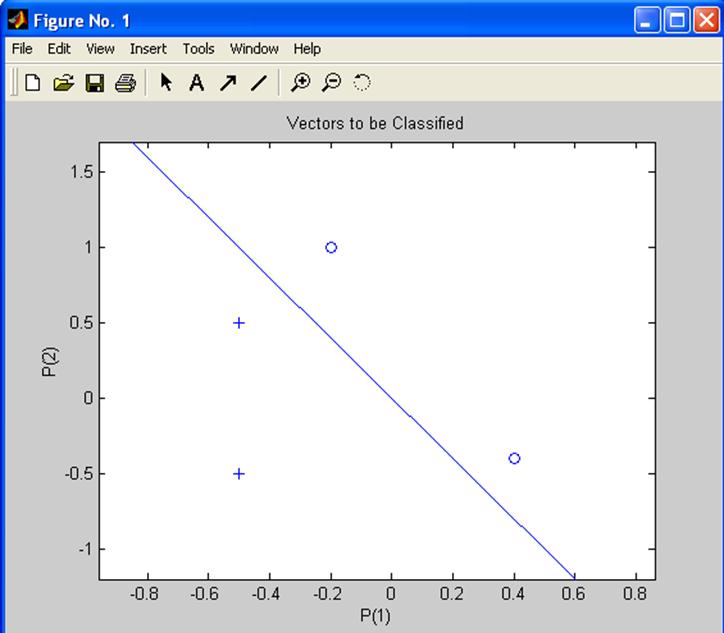
Функция adapt возвращает новый объект — сеть, которая выполняет классификацию, выход сети и ошибку.

Проведем классификацию нового вектора с помощью обученного нейрона на основе функции sim. Определим но­вый вектор р.

\\   определение вектора  Р

Р =   [0. 6;   1. 1];

\\ имитация работы нейрона net, получение отклика

нейрона а

а  = sim (net,  P);                                                                       

\\  изображение входа P,   отнесенного нейроном                

к категории а                                                

plotpv(P,   а);                     

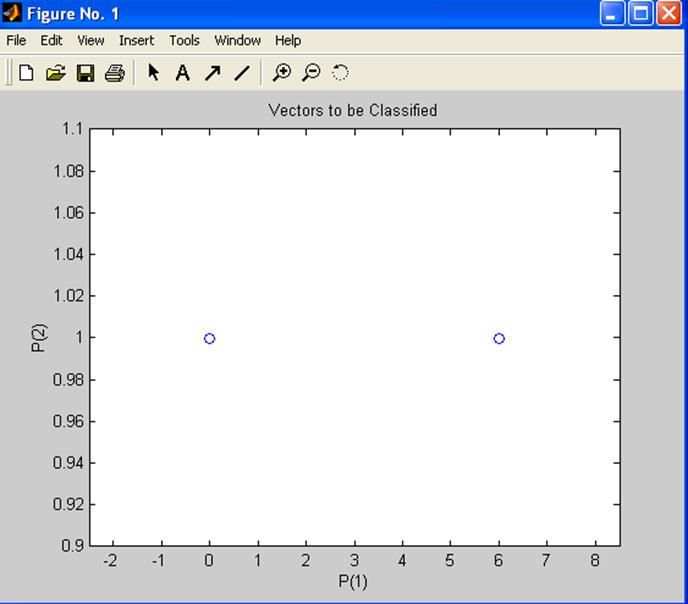
Обученный нейрон можно использовать для классифика­ции любого вектора

\\   включить режим добавления графиков  в графическом окне

holdon;

\\  изображение входных точек в  соответствии с категориями Т

plotpv(P,   T) ;

\\  изображение разделяющей поверхности

plotpc (net. IW {1},   net.b{1});

\\   отключение режима добавления графиков

holdoff;

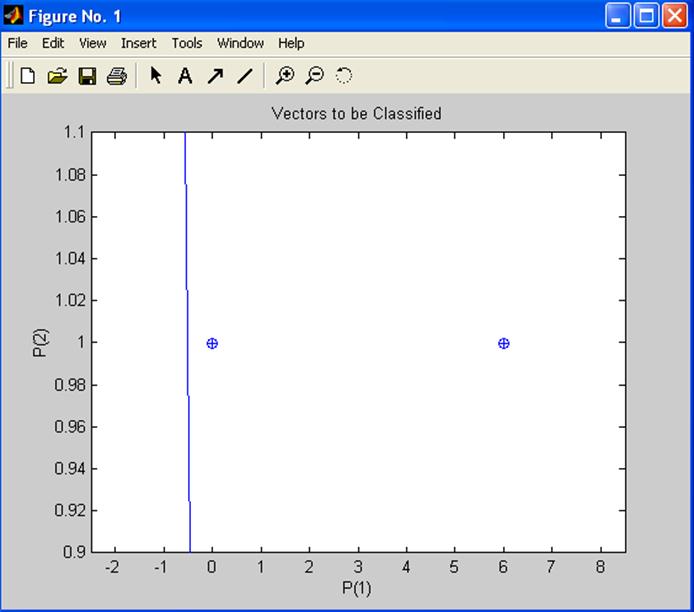
Нейрон классифицирует новую точку, как принадлежа­щую категории «0» (представлена кружком), а не категории «1» (представлена +).

Пример 7. Создание слоя линейных нейронов

Рассмотрим последовательность из 10 шагов (для выхода T1, который известным образом зависит от входов Р1):

\\  последовательность  входов

Р1   =   {-1   0  0  0  1   1   -1   0  -1   1} ;

\\   последовательность  выходов

Т1   =   {-1   -1   1   0  1   2  0  -1   -1   1};

Используем функцию newlin, чтобы создать нейрон со зна­чениями входа в интервале [-1; 1], задержками входа от 0 до 1 и уровнем обучения 0,1.

\\ создание линейного слоя из одного нейрона со значениями входа в интервале [-1; 1], задержками входа от 0 до 1 и уровнем обучения 0,1.

net = newlin([-1 1], 1, [0 1], 0.1);

Адаптируем нейрон к задаче одним проходом через последовательность входа. Измерим среднюю квадратичную ошибку с помощью функции mse(e).                                           

\\   адаптация нейрона  к последовательности p1            

[net,  у,   е, pf]  = adapt (net,   P1,   T1);                        

\\  измерение ошибки

mse (e);

Получим довольно большую ошибку. Вновь адаптируем сеть на 10 шагах последовательности, используя предыдущее значение Pf как новое исходное значение задержки:

р2  =   {1   -1   -1   1   1   -1   0  0  0  1};

t2  =   {20-2020-1 0 0 1};