net.trainParam.goal 0 целевое значение ошибки
net.trainParam.max_fail 5 максимальное значение ошибки
net.trainParam.mem_reduc 1 фактор оптимизации процесса обучения:
оптимизация использования памяти или
времени процессора
net.trainParam.min_grad минимальное значение градиента
le-10
net.trainParam.show 25 количество эпох между показами
net.trainParam.time inf максимальное время обучения в секундах
TR структура данных, содержащая значения об
обученности НС в текущую эпоху
TR.epoch номер эпохи
TR.perf уровень обученности (Trainingperformance)
TR.vperf степень качества (Validationperformance)
TR.tperf результативность обработки теста
(Testperformance)
TR.mu значение адаптивности
Структура данных описания адаптированной НС
net.adaptfcn включает в себя следующие поля net.adapt.param:
NET — адаптированная НС;
Y — выходы НС;
Е — ошибки НС;
Pf — окончательные входные значения задержек;
Af — окончательные выходные задержки;
TR — результат обучения (эпохи и целевая ошибка).
Проведем в среде Matlab toolbox эксперименты, используя рассмотренные функции.
Пример 1. Создание нейрона,
выполняющего функцию логического И
Создадим нейрон с одним двухэлементным входом (интервалы первого и второго элементов [0; 1]). Определим два первых параметра функции newp, а в качестве значений третьего и четвертого параметра (типа ФА и имени процедуры обучения) воспользуемся значениями по умолчанию.
\ \ создание нейрона с одним двухэлементным входом (интервал первого элемента [0; 1] и интервал второго элемента [-2; 2]
net = newp([0 1; -2 2], 1);
Для того чтобы исследовать поведение нейрона, необходимо имитировать его работу с помощью функции sim. Для определения последовательности значений входа создадим последовательность Р1.
\\ создание последовательности значений входа
Р1 = {[0; 0] [0; 1] [1; 0] [1; 1]};
\\ имитация работы нейрона net на последовательности входов Р1 желаемых выходов — Т, которая позволит нам провести адаптацию нейрона (обучить его) через 20 проходов.
Y = sim (net, P1);
\\ создание последовательности выходов
Т1 = {0, 0, 0, 1} ;
\\ установка количества проходов (циклов) адаптации
net.adaptParam.passes = 20;
\\ адаптация нейрона net для обучающей выборки <Р1;Т>
net = adapt (net, P1, T1) ;
\\симуляция работы нейрона net на последовательности входов Р1
Y = sim (net, P1) ;
В результате мы получим нейрон, выполняющий функцию логического И.

Пример 2. Обучение нейрона выполнению функции логического ИЛИ
Для переобучения нейрона на выполнение функции ИЛИ переопределим входы Р и выходы Т.
\\ создание последовательности входов
Р2 = [0 0 1 1; 0 1 0 1];
\\ создание последовательности выходов (реакций) для нейрона, выполняющего функцию логического ИЛИ
Т2 = [0, 1, 1, 1];
Инициализируем нейрон, обучим его на 20 проходах (эпохах)
\\ инициализация нейрона net
net = init (net) ;
\\ имитация работы нейрона net на последовательности
входовР2
Y = sim (net, P2) ;
\\ установка количества проходов
net. trainParam.epochs = 20;
\\ обучение нейрона net на обучающей выборке <Р2, Т2>
net = train (net, Р2, Т2) ;
\ \ имитация работы нейрона net на последовательности входов Р2
Y = sim (net, P2);

Для случайного изменения весов и порога срабатывания используем функцию init. По умолчанию для создаваемого нейрона указана функция hardlim.
Пример 3. Определение входов со случайными значениями
Определим случайный вход Р и ошибку Е для нейрона с двухэлементным входом.
\\ определение входа р как вектора двух случайных чисел из интервала [0; 1]
р = rand (2,1) ;
\\ определение входа е как случайного числа из интервала [0; 1]
е = rand (1,1) ;
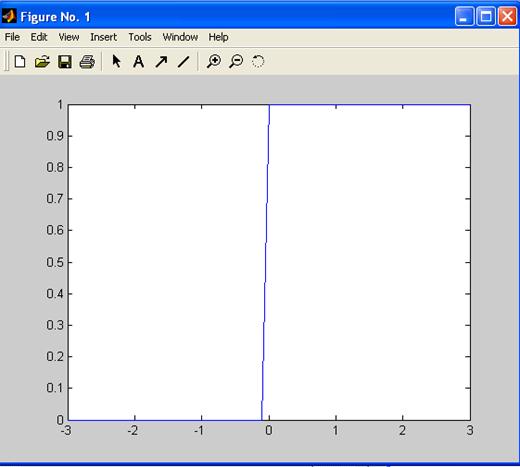
Пример 4. Получение графика функции активации hardlim
Получим график функции активации для интервала [-3; +3] с шагом 0.1.
\\ определение переменной n со значениями из интервала [-3; 3] с шагом 0.1
n = -3 : 0.1 : 3;
\\ вычисление пороговой функции от переменной n
b = hardlim (n) ;
\\ изображение графика функции b = hardlim(n)
plot (n, b) ;
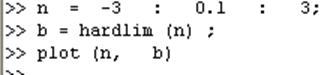
Пример 5. Имитация работы линейного нейрона
Создадим с помощью newp нейрон с двухэлементным входом (значения входа в интервале [0; 1]) net= newp([0 1;0 1],1). Функция sim имитирует работу нейрона для отдельного вектора и для трех векторов.
\\ определение двухэлементного вектора
p1 = [.3; .7];
\\ имитация работы нейрона net на входном векторе
результат имитации — вектор a1
a1 = sim (net, p1);
\\определение матрицы входов размерностью 3 на 2
(три двухэлементных вектора)
р2 = [.3 .5 .2; .8 .5 .4];
\\ имитация работы нейрона net на входном векторе р2,
результат имитации — вектор а2
а2 = sim (net, p2);

Пример 6. Обучение нейрона классификации векторов на две категории
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.