По классической электромагнитной теории простейшей системой, которая может излучать электромагнитные волны, является электрический диполь, дипольный момент которого p = qd не постоянен во времени. На практике изменение дипольного момента может быть вызвано как изменением заряда q, что характерно для антенн радиодиапазона, так и изменением эффективного размера диполя d в классической модели атома.
Из уравнений Максвелла следует, что амплитуды электрического и магнитного полей волны оказываются пропорциональными второй производной дипольного момента по времени. В точке, отстоящей от колеблющегося диполя на расстояние r >> l (так называемая дальняя или волновая зона), поле определяется выражением
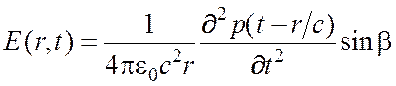, (1.1)
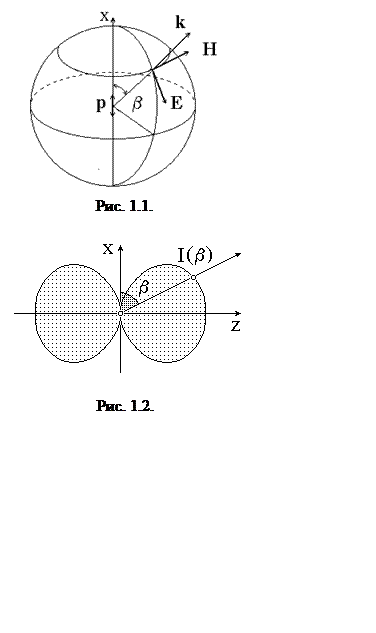
где b – угол между осью диполя и направлением на точку наблюдения (рис. 1.1).
Отметим ряд важных следствий,
вытекающих из формулы (1.1). Во-первых, при гармоническом изменении дипольного
момента p = p0 cos (w0t),
амплитуды полей оказываются пропорциональными квадрату частоты w02, а интенсивность
излучения – четвертой степени частоты: I ~ w04.
Во-вторых, имеется зависимость интенсивности излучения от направления: I = I0 sin2b, что иллюстрирует рис. 1.2. Максимальная интенсивность наблюдается в экваториальной плоскости при b = p/2, а вдоль своей оси диполь не излучает. Эти зависимости играют важную роль в теории рассеяния света, обсуждаемой позже.
В-третьих, волновой фронт, т. е. поверхность постоянной фазы, представляет собой сферу. Таким образом, точечный источник (точнее источник, размеры которого малы по сравнению с длиной волны) всегда излучает сферические волны. Плоская волна, характеризующаяся определенным направлением распространения, является математической абстракцией, приближением, применимым при очень больших радиусах волнового фронта.
Поскольку колеблющийся диполь теряет энергию на излучение, его колебания затухают. Уравнение затухающих колебаний хорошо известно, оно имеет вид:
, (1.2)
где g – так называемый коэффициент радиационного трения, учитывающий потери на излучение. Решая уравнение (1.2) при условии w0 >> g, находим (с учетом (1.1)) для излучаемой волны:
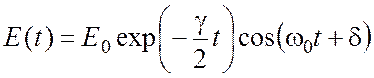. (1.3)
Изменение амплитуды со временем приводит к нарушению монохроматичности волны и появлению новых частот в ее спектре F(w). По теореме Фурье
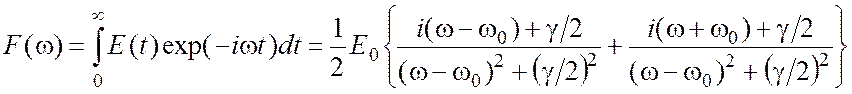. (1.4)
Переходя от напряженности поля к интенсивности, получаем:
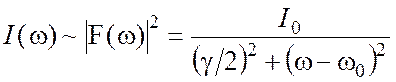. (1.5)
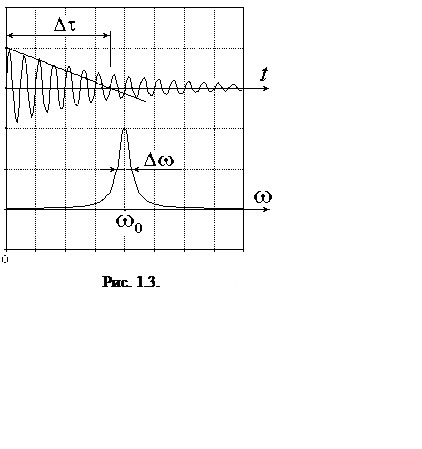
В этом случае распределение энергии по частотам I(w) соответствует лоренцевскому контуру (рис. 1.3), ширина которого на половине высоты определяется коэффициентом затухания g. Эта величина называется естественной шириной спектральной линии.
Dwест = g. (1.6)
В соответствии с классической теорией коэффициент
затухания зависит только от частоты излучения и равен 
.
Для излучателя оптического диапазона (l =
0,6 мкм, w0 =
3×1015 с-1)
естественная ширина линии имеет порядок 108 с-1,
а добротность атомного осциллятора Q = w0 ¤ g ~ 107. Поскольку переменные
самой функции и ее спектра (в данном случае – время и частота) являются сопряженными,
то для произведения времени затухания t
и ширины спектра Dw выполняется
универсальное ограничение: t×Dw » 2p.
Таким образом, амплитуда колебаний уменьшается вдвое за несколько миллионов
периодов. Тем не менее, можно считать, что излучение отдельного атома
представляет собой волновой цуг конечной длительности t.
Современная квантовая теория позволяет значительно более строго и точно рассчитать спектральные характеристики излучаемого атомом света, однако основные качественные результаты совпадают с классическими: линия имеет лоренцевскую форму с типичной естественной шириной Dwест ~ 108 с-1
Соотношение между шириной спектра и резонансной частотойDw << w0 определяет условие квазимонохроматичности света (для монохроматического света считают Dw = 0).
Ширина линии излучения реальных источников света обусловлена не только радиационным затуханием, но и рядом других физических эффектов. Один из них – столкновения излучающих атомов с окружающими их атомами и молекулами. При таких столкновениях может произойти обрыв излучаемого волнового цуга или скачок фазы излучения. И в том и в другом случае эффективная длительность цуга t уменьшается и, соответственно, возрастает ширина спектра (рис. 1.4).При фиксированных давлении итемпературе t статистически одинаково для всех атомарных излучателей. Можно показать, что в газоразрядном источнике света с максвелловским распределением атомов по скоростям спектральная линия описывается лоренцевским контуром, аналогичным (1.5), но с шириной Dw = g+gст, где gст –уширение, определяемое числом столкновений в единицу времени. Из кинетической теории Максвелла следует, что
, (1.7)
где NA – число Авогадро, p, T, m – давление, температура и молярная масса газа, s2 – сечение столкновений, параметр по порядку величины близкий к геометрическому размеру молекул и характеризующий вероятность обрыва волнового цуга.
Расчеты показывают, что при давлении порядка 10 мм рт. ст. столкновительное уширение в несколько раз превышает естественную ширину линии. Проводя измерения ширины линии при различных давлениях (рис. 1.5) и экстраполируя результаты к нулевому давлению, можно определить естественную ширину, а из наклона – сечение столкновений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
