Отражение и преломление света (Граничные условия. Формулы Френеля. Полное внутреннее отражение. Отражение света от поверхности металлов)

ОТРАЖЕНИе И ПРЕЛОМЛЕНИе света

1.1.  Граничные условия. Формулы Френеля

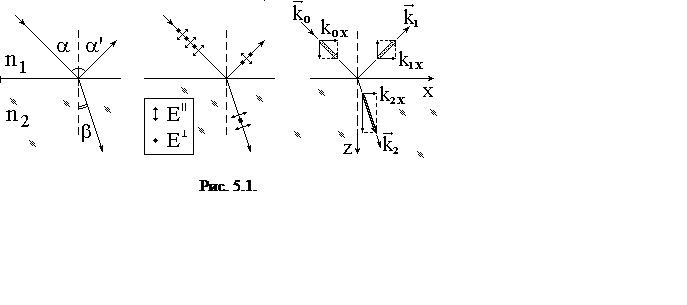
Классической задачей, для решения которой оказывается важной ориентация вектора Е, является прохождение световой волны через границу раздела двух сред. В силу геометрии задачи возникает разница в отражении и преломлении двух независимых компонент, поляризованных параллельно и перпендикулярно плоскости падения, и, следовательно, исходно неполяризованный свет после отражения или преломления становится частично поляризованным.

Граничные условия для векторов напряженности и индукции, известные из электростатики, уравнивают на границе раздела тангенциальные компоненты векторов Е и H и нормальные компоненты векторов D и B, по сути, выражая отсутствие токов и зарядов вдоль границы и ослабление внешнего электрического поля в e раз при попадании в диэлектрик:

.                                                                     (5.1)

При этом поле в первой среде складывается из полей падающей и отраженной волн, а во второй среде – равно полю преломленной волны (см. рис. 2.1).

Поле в любой из волн может быть записано в виде соотношений типа . Т. к. граничные условия (5.1) должны выполняться в любой точке границы раздела и в любой момент времени, из них можно получить законы отражения и преломления:

1.  Частоты всех трех волн одинаковы: w₀ = w₁ = w₂.

2.  Волновые вектора всех волн лежат в одной плоскости:.

3.  Угол падения равен углу отражения: a = a'.

4.  Закон Снеллиуса: . Можно показать, что произведение n×sin a остается постоянным при любом законе изменения показателя преломления вдоль оси Z, не только ступенчатом на границах раздела, но и непрерывном.

На эти законы поляризация волн не влияет.

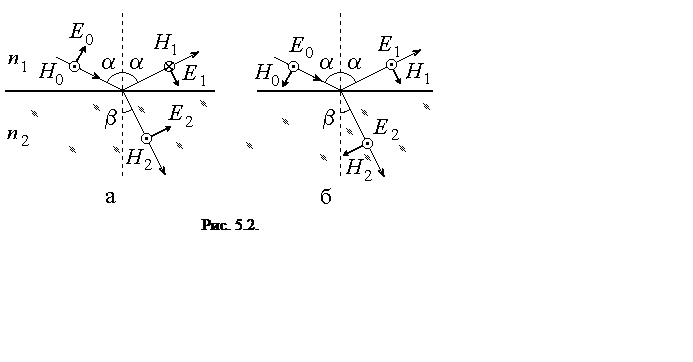
C другой стороны непрерывность соответствующих компонент векторов Е и H приводит к так называемым формулам Френеля, позволяющим рассчитать относительные амплитуды и интенсивности отраженной и прошедшей волн для обеих поляризаций. Выражения оказываются существенно различными для параллельной (вектор E лежит в плоскости падения) и перпендикулярной поляризации, естественно, совпадая для случая нормального падения (a = b = 0).

Геометрия полей для параллельной поляризации показана на рис. 5.2а, для перпендикулярной – на рис. 5.2б. Как было отмечено в разделе 4.1, в электромагнитной волне вектора E, H и k образуют правую ортогональную тройку. Поэтому если тангенциальные компоненты векторов E₀ и E₁ падающей и отраженной волн направлены одинаково, то соответствующие проекции магнитных векторов имеют разные знаки. С учетом этого, граничные условия приобретают вид:

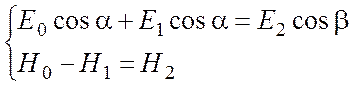                                     (5.2)

для параллельной поляризации и

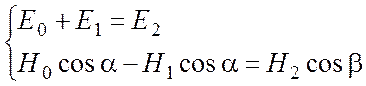                                   (5.3)

для перпендикулярной поляризации. Кроме того, в каждой из волн напряженности электрического и магнитного полей связаны соотношениями . С учетом этого, из граничных условий (5.2) и (5.3) можно получить выражения для амплитудных коэффициентов отражения и пропускания:

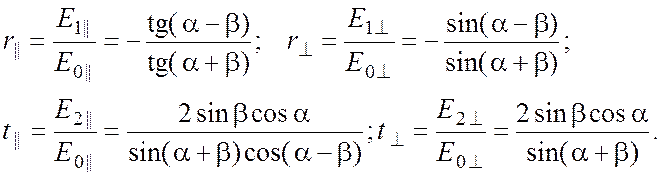                                                                     (5.4)

Помимо амплитудных, представляют интерес энергетические коэффициенты отражения R и пропускания T, равные отношению потоков энергии соответствующих волн. Т. к. интенсивность световой волны пропорциональна квадрату напряженности электрического поля, для любой поляризации выполняется равенство .Кроме того, справедливо соотношение R + T = 1, выражающее закон сохранения энергии при отсутствии поглощения на границе раздела. Таким образом,

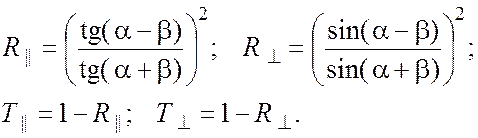                   (5.5)

Совокупность формул (5.4), (5.5) и называется формулами Френеля. Особый интерес представляет предельный случай нормального падения света на границу раздела (a = b = 0). При этом исчезает различие между параллельной и перпендикулярной поляризациями и

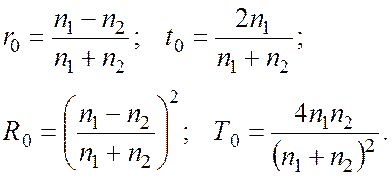                               (5.6)

Из (5.6) находим, что при нормальном падении света из воздуха (n₁ = 1) на стекло (n₂ = 1.5) отражается 4% энергии светового пучка, а проходит 96%.

1.2.  Анализ формул Френеля

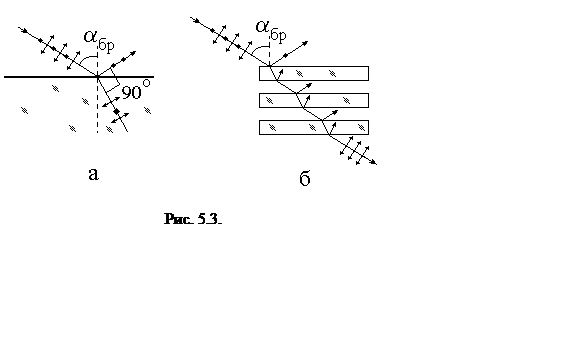
Рассмотрим сначала энергетические характеристики. Из (5.5) видно, что при a + b = p/2 коэффициент отражения параллельной компоненты обращается в нуль: R _|| = 0. Угол падения, при котором возникает этот эффект, называется углом Брюстера. Из закона Снеллиуса легко найти, что

,                                                    (5.7)

где n₁₂ – относительный показатель преломления. В то же время для перпендикулярной компоненты R _^ ¹ 0. Поэтому при падении неполяризованного света под углом Брюстера отраженная волна оказывается линейно поляризованной в плоскости, перпендикулярной плоскости падения, а прошедшая – частично поляризованной с преобладанием параллельной компоненты (рис. 5.3а) и степенью поляризации

.

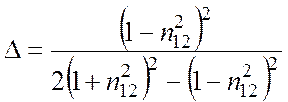Для перехода воздух-стекло угол Брюстера близок к 56^о.

На практике получение линейно поляризованного света за счет отражения под углом Брюстера используется редко из-за низкого коэффициента отражения. Однако возможно построение поляризатора, работающего на пропускание, с использованием стопы Столетова (рис. 5.3б). Стопа Столетова состоит из нескольких плоскопараллельных стеклянных пластинок. При прохождении через нее света под углом Брюстера, перпендикулярная компонента практически полностью рассеивается на границах раздела, а прошедший луч оказывается поляризован в плоскости падения. Такие поляризаторы используются в мощных лазерных системах, когда поляризаторы других типов могут быть разрушены лазерным излучением. Другим применением эффекта Брюстера является снижение потерь на отражение в лазерах за счет установки оптических элементов под углом Брюстера к оптической оси резонатора.

Вторым важнейшим следствием формул Френеля является существование полного внутреннего отражения (ПВО) от оптически менее плотной среды при углах падения больших, чем предельный угол, определяемый из соотношения

.                                                 (5.8)

Подробно эффект полного внутреннего отражения будет рассмотрен в следующем разделе, сейчас отметим только, что из формул (5.7) и (5.8) следует, что угол Брюстера всегда меньше предельного угла.

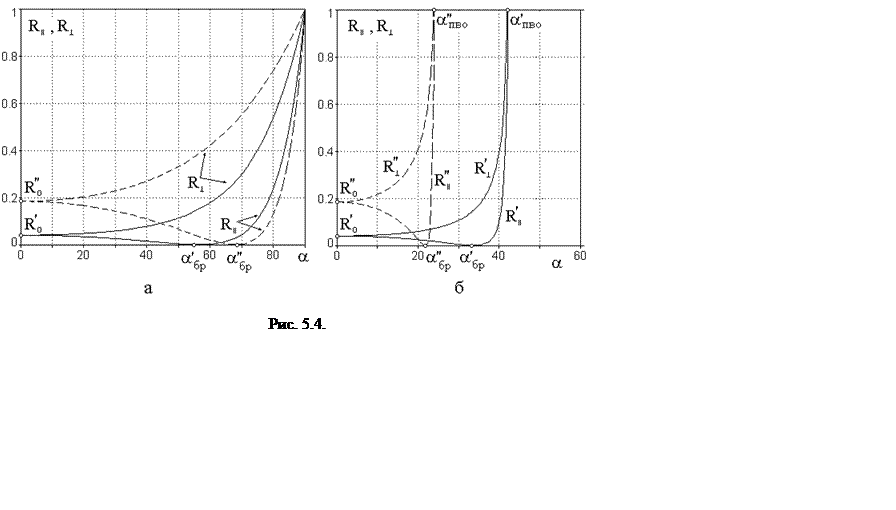На графиках рис. 5.4а приведены зависимости коэффициентов отражения при падении света из воздуха на границы со средами с n₂' = 1.5 (сплошные линии) и n₂'' = 2.5 (штриховые линии). На рис. 5.4б направление прохождения границы раздела обратное.

Обратимся теперь к анализу амплитудных коэффициентов (5.4). Нетрудно видеть, что при любых соотношениях между показателями преломления и при любых углах коэффициенты пропускания t положительны. Это означает, что преломленная волна всегда софазна падающей.

Коэффициенты отражения r, напротив, могут быть отрицательны. Поскольку всякую отрицательную величину можно записать как , отрицательность соответствующего коэффициента можно интерпретировать как сдвиг фазы на p при отражении. Об этом эффекте часто говорят также как о потере полволны при отражении.

Из (5.4) следует, что при отражении от оптически более плотной среды (n₁ < n₂, a > b) r_^ < 0 при всех углах падения, а r _|| < 0 при углах падения меньших угла Брюстера. При отражении от оптически менее плотной среды (n₁ > n₂, a < b) отражение софазное за исключением случая падения света с параллельной поляризацией под углом большим угла Брюстера (но меньшим предельного угла). Очевидно, что при нормальном падении на оптически более плотную среду фаза отраженной волны всегда сдвинута на p.

Таким образом, естественно поляризованный свет при прохождении границы раздела двух сред превращается в частично поляризованный, а при отражении под углом Брюстера даже в линейно поляризованный. Линейно поляризованный свет при отражении и преломлении остается линейно поляризованным, но ориентация плоскости поляризации может измениться из-за различия коэффициентов отражения двух компонент.

1.3.  Полное внутреннее отражение