Отражение и преломление света (Граничные условия. Формулы Френеля. Полное внутреннее отражение. Отражение света от поверхности металлов), страница 2

При падении света на оптически менее плотную среду (например, переход стекло – воздух) угол преломления больше, чем угол падения. При угле падения, называемом предельным углом и определяемым формулой (5.7) , sin b = 1, т. е. b = 90^о.  Для границы стекло (n₁ = 1.5) – воздух a_пво » 42^о.

Если же a > a_пво, то формально вычисленный синус угла преломления становится больше 1, что возможно только при комплексных углах. Разумеется, все реальные углы, образуемые световыми лучами с осями координат, остаются вещественными, но меняется физическая сущность происходящих процессов.

При a > a_пво формально вычисленные величины , 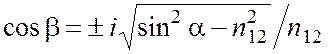. Следовательно, волновой вектор преломленной волны становится комплексным и поле во второй среде может быть записано как

,                             (5.9)

где 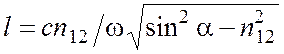; v₂ – скорость света во второй среде. Соотношение (5.9) означает, что электромагнитное поле во второй среде представляет собой неоднородную волну, распространяющуюся параллельно границе раздела, с амплитудой, убывающей по мере удаления от границы. Величина l, по порядку близкая к длине волны, характеризует эффективную глубину проникновения поля во вторую среду. Таким образом, при полном внутреннем отражении электромагнитное поле во второй среде существует только в тонком приповерхностном слое.

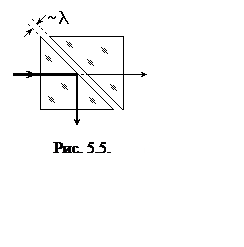
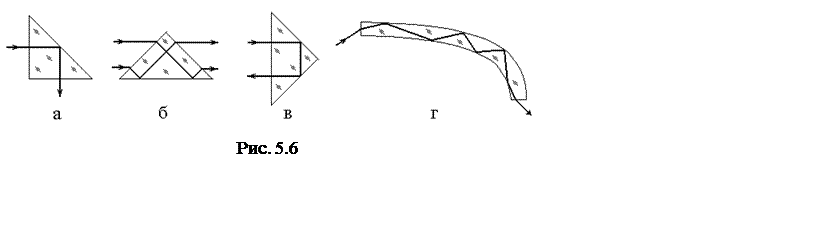
Если две стеклянные призмы поместить близко друг от друга, как показано на рис. 5.5, то неоднородная преломленная волна попадает во вторую призму и часть светового пучка проходит не отражаясь. Возникает нарушенное полное внутреннее отражение (НПВО). Изменяя толщину воздушного зазора, можно менять соотношение интенсивностей отраженной и прошедшей волн, т. е. получить модулятор света. Аналогом НПВО является туннельный эффект в квантовой механике.

Используя формулы Френеля (5.4) и подставляя в них значения sin b и cos b, найдем амплитудные коэффициенты отражения при углах падения больших предельного:

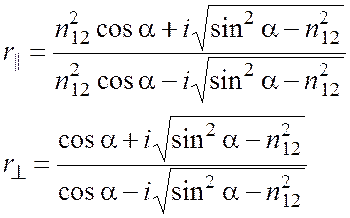.                                  (5.10)

Коэффициенты отражения становятся комплексными, причем для любой поляризации R = |r |² = 1. Таким образом, при полном внутреннем отражении вся световая энергия возвращается обратно в первую среду. Этот эффект находит многочисленные применения в оптических устройствах. На рис. 5.6 показаны примеры призм ПВО: поворачивающей (а), оборачивающей (б), отражающей (в). Полное отражение используется также в оптических световодах, представляющих собой тонкое стеклянное волокно, по которому свет может распространяться на значительные расстояния (рис. 5.6г). Световоды широко применяются в оптических линиях связи, медицине и других областях.

Всякое комплексное число можно записать в показательной форме: . Тот факт, что коэффициенты отражения (5.10) стали комплексными, означает наличие фазового сдвига между отраженной и падающей волнами. Этот сдвиг не одинаков для двух поляризаций, причем d _|| ³ d_^. Поэтому в отраженной волне появляется дополнительный фазовый сдвиг d = d _|| - d_^ между параллельной и перпендикулярной компонентами электрического вектора, определяемый соотношением

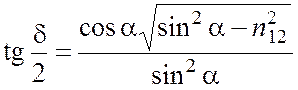.                                         (5.11)

Фазовый сдвиг достигает максимума, равного

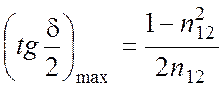                                                     (5.12)

при угле падения

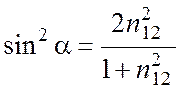.                                                          (5.13)

Из формул (5.11) – (5.13) вытекает, что после полного внутреннего отражения состояние поляризации света может измениться. Так линейно поляризованный свет превращается в поляризованный по эллипсу. Этот эффект используется, в частности, для получения циркулярно поляризованного света. Однако получить необходимый для этого фазовый сдвиг p/2 можно, как следует из (5.12), только если показатель преломления первой среды не меньше 2.41. В видимой области такой показатель преломления имеет только алмаз. 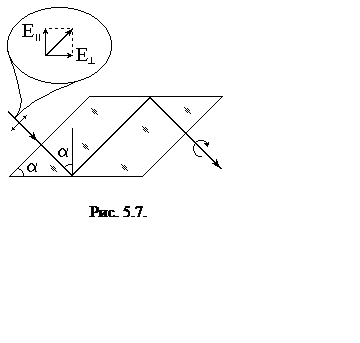Френелем было предложено использовать призму (ромб Френеля), в которой свет испытывает полное внутреннее отражение дважды (рис. 5.7). Для стекла с n = 1.5 фазовый сдвиг p/4 достигается при углах падения 48^о37' и 54^о37'. Если угол при вершине ромба Френеля равен одному из этих углов, а плоскость поляризации падающего света образует угол 45^о или 135^о с плоскостью падения, то выходящий свет будет поляризован по правому или левому кругу.

1.4.  Отражение света от поверхности металлов

Последовательная теория, описывающая распространение электромагнитных волн в проводниках, должна учитывать колебания свободных электронов, плотность которых в металлах весьма высока. Однако, основные оптические свойства металлов и других проводящих сред могут быть описаны на основе классической электромагнитной теории.

Все отличие проводников от диэлектриков с точки зрения теории Максвелла заключается в ненулевой величине слагаемого, содержащего плотность тока проводимости в уравнении

.

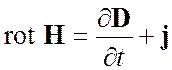Для квазимонохроматических волн операция дифференцирования по времени сводится к умножению на iw. С учетом закона Ома , где s – удельная проводимость среды, получаем:

                                                    (5.14)

Вводя комплексную диэлектрическую проницаемость

,                                                            (5.15)

уравнение (5.14) можно формально привести к такому же виду, как для диэлектриков: . Из (5.15) видно, что мнимая часть комплексной диэлектрической проницаемости обусловлена проводимостью среды.

Естественно, что комплексным становится и показатель преломления проводящей среды: . Так же как и у диэлектриков, мнимая часть показателя преломления описывает поглощение света (см. раздел 2.2). Глубина проникновения поля в среду, как это вытекает из закона Бугера (2.3) равна . Для большинства металллов в видимой области (nk) = 3…5, т. е. глубина проникновения составляет доли длины волны. Даже очень тонкие металлические пленки непрозрачны для света.

Приравнивая вещественные и мнимые части соотношения , находим:

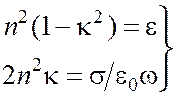.                                                           (5.16)

Отсюда следует, что для идеального проводника (s®¥) n®¥, k = 1.

Проанализируем теперь поведение отраженной от поверхности металла волны. Воспользуемся формулами Френеля для нормального падения (5.6), заменив в них n на ñ:

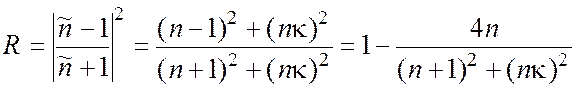. (5.17)

Отсюда видно, что при больших n коэффициент отражения стремится к 1. То, что металлические слои являются хорошими зеркалами всем известно хотя бы на бытовом уровне. Таким образом, несмотря на то, что металлы обладают высоким коэффициентом поглощения, реального поглощения света практически не происходит – электромагнитное поле просто не проникает в проводник.

Для неидеального проводника с n >> 1, k » 1 из (5.17) с учетом второго уравнения (5.16) коэффициент отражения отличается от единицы на величину

.                                             (5.18)

Это означает, что потери при отражении растут с ростом частоты, т. е. с уменьшением длины волны. Кроме того, с ростом частоты проводимость среды падает. Поэтому металлические зеркала, прекрасно отражающие ИК излучение, в видимой области отражают значительно хуже, а в УФ диапазоне коэффициент отражения металлических зеркал не превышает 20…30%. Единственным способом создания высокоотражающих (на уровне 99%) зеркал для видимой и УФ областей является использование многослойных интерференционных покрытий.

Вследствие того, что показатель преломления металлов комплексный, комплексными становятся и амплитудные коэффициенты отражения при наклонном падении света. Так же, как и при полном внутреннем отражении (см. раздел 5.3) возникает дополнительная разность фаз между параллельной и перпендикулярной составляющими электрического вектора, т. е. линейно поляризованный свет после отражения превращается в эллиптически поляризованный. Представив комплексный коэффициент отражения в виде , сравним угловые зависимости параметров и  для диэлектрика с n = 2 (рис. 5.8а) и проводника с n = 2, k = 1 (рис. 5.8б). Как видно, у проводников отсутствует угол полной поляризации, хотя коэффициент отражения параллельной компоненты всегда больше, чем перпендикулярной. Нет также резкого скачка фазы при угле Брюстера.