Прохождение оптических импульсов по многомодовым волоконным световодам. Исследование прохождения световых импульсов по многомодовым волоконным световодам, страница 17

Для направляемых лучей величина первого инварианта должна удовлетворять условию:

            (5)

Следует отметить, что показатель преломления зависит от длины волны. На рис. 4 показаны зависимости n(λ) для чистого кварца (черная кривая) и для кварца с различным содержанием легирующей добавки GeO₂.

Рис. 4. Зависимости показателя преломления от длины волны (1 – чистый кварц, 2 – 8.1% GeO2, 3 – 11.0% GeO2, 3 – 13.1% GeO2).

 Межмодовая дисперсия в ВС с усеченным степенным профилем.

Известно, что удельное время распространения луча на единичное расстояние в ВС с усеченным степенным профилем зависит только от лучевого инварианта В и от параметра р внеосевой дисперсии материала сердцевины ВС:

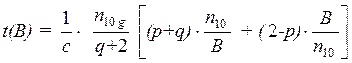,                                                             (6)

где 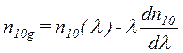 - групповой показатель преломления[4] на оси ВС;

км/с - скорость света в вакууме;

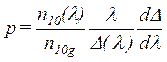 - параметр внеосевой дисперсии материала сердцевины ВС.

На рис. 5 показана зависимость удельного времени распространения для различных значений первого инварианта В для ВС с n₁₀=1.5, n₂=1.485, p=0.1 и q=1.79. Из рис. 5 видно, что для определенного значения первого инварианта удельное время распространения принимает минимальное значение. Можно найти значение первого инварианта В_m, которому соответствует минимальное удельное время распространения. Для этого надо взять первую производную от выражения (6) по В и приравнять ее к нулю.

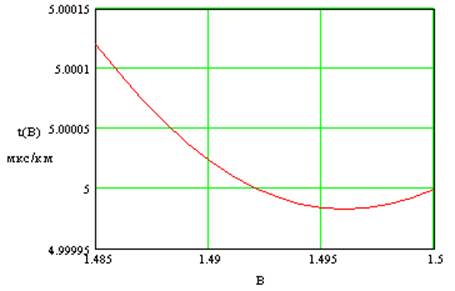
Рис. 5. Зависимость удельного времени задержки от величины первого инварианта.

Несложные расчеты позволяют получить величину В_m

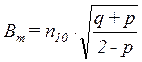.                                                                                                       (7)

При этом минимальное удельное время распространения на единичное расстояние будет равно:

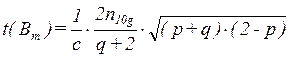                                                                          (8)

Если рассчитанное значение В_m не удовлетворяет условию направляемых лучей (5), то и расчет минимального удельного времени распространения по этой формуле не имеет смысла. В этом случае минимальное t_min и максимальное t_max удельное время распространения соответствуют минимальному и максимальному значениям инварианта В.

В качестве верхней оценки межмодовой дисперсии D_м принимается разность максимального t_max и минимального t_min удельных времен распространения из трех значений t(n₁₀), t(n₂)и t(B_m), если В_m удовлетворяет условию (5), или из двух значений t(n₁₀) и t(n₂), если В_m не удовлетворяет условию (5):

.                                                                                                           (9)

Можно также утверждать, что минимальной межмодовой дисперсии D_мсоответствует равенство удельных времен распространения для минимального и максимального значения первых инвариантов

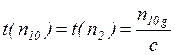,                                                                                                (10)

На рис. 6 для этого случая показана зависимость удельного времени распространения от значений первого инварианта В для ВС с теми же параметрами, что и на предыдущем рис. 6, но с другим значением q=1.781.

Решение уравнения (10) позволяет получить оптимальное значение параметра степенного профиля

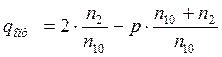.                                                                                       (11)

Минимально достижимую межмодовую дисперсию при q= q_опт можно рассчитать преобразовав выражение (9) к следующему виду

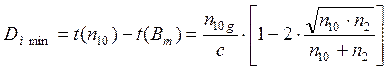
                                        (12)

Для приведенных выше параметров B_m=1.492, q_opt=1.781, D_мmin=63 пс/км.

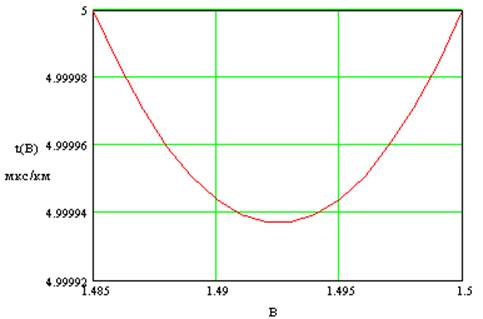
Рис. 6. Зависимость удельного времени задержки от величины первого инварианта для оптимального показателя степенного профиля

Зависимость межмодовой дисперсии от показателя профиля q имеет резкий минимум, который также зависит от длины волны (рис. 7).

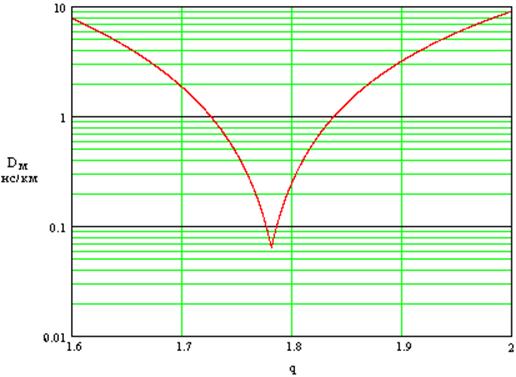
Рис. 7. Зависимость межмодовой дисперсии от показателя степенного профиля

Межмодовая дисперсия в реальных градиентных ВС с профилем близким к оптимальному значительно меньше, чем у ступенчатых ВС и составляет 0.2-2 нс/км.