








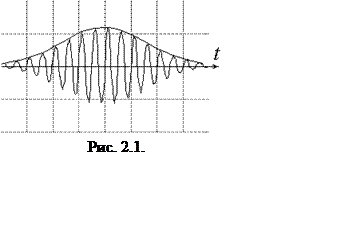
 Поскольку волновой пакет, или цуг
волн оказывается суперпозицией гармоник с различными частотами,
возникает вопрос о поведении этих волн в среде распространения. Представим
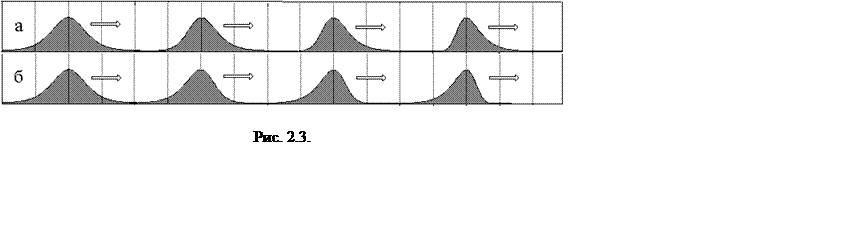
волновой пакет в виде импульса, длительность которого значительно превышает
период колебаний электромагнитного поля в световой волне (рис. 2.1). Из-за
инерционности любой фотоприемник не реагирует на мгновенную величину поля.
Поэтому при измерениях скорости света реально регистрируется скорость
распространения медленно меняющейся огибающей импульса, а не заполняющей его
высокочастотной синусоиды.
Поскольку волновой пакет, или цуг
волн оказывается суперпозицией гармоник с различными частотами,
возникает вопрос о поведении этих волн в среде распространения. Представим
волновой пакет в виде импульса, длительность которого значительно превышает
период колебаний электромагнитного поля в световой волне (рис. 2.1). Из-за
инерционности любой фотоприемник не реагирует на мгновенную величину поля.
Поэтому при измерениях скорости света реально регистрируется скорость
распространения медленно меняющейся огибающей импульса, а не заполняющей его
высокочастотной синусоиды.
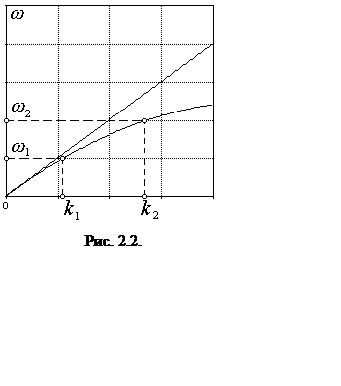 Можно показать, что скорость
монохроматической волны, определяемая как скорость перемещения волнового фронта,
т. е. поверхности равной фазы, (фазовая скорость) равна
Можно показать, что скорость
монохроматической волны, определяемая как скорость перемещения волнового фронта,
т. е. поверхности равной фазы, (фазовая скорость) равна ![]() , а скорость импульса как целого (групповая
скорость) –
, а скорость импульса как целого (групповая
скорость) –
![]() . (2.1)
. (2.1)
Для вакуума обе эти величины совпадают, поскольку частота и волновое число связаны соотношением w = ck, но в любых других средах эта зависимость более сложная. Функцию w = w(k) (рис. 2.2) можно определить, зная дисперсию среды, т. е. зависимость показателя преломления от длины волны или частоты: n = n(w) или n = n(l). Найдем связь групповой и фазовой скорости:
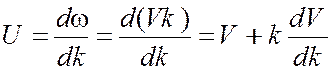 .
.
Переходя к независимой переменной l с учетом соотношения k = 2p/l, приходим к формуле Рэлея
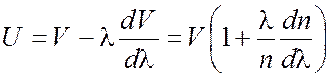 . (2.2)
. (2.2)
Очевидно, возможны три случая:
1. ![]() . Дисперсия отсутствует. Строго говоря,
эта ситуация реализуется только в вакууме, но на практике бывает, что
дисперсией можно пренебречь, например, при распространении света в воздухе;
. Дисперсия отсутствует. Строго говоря,
эта ситуация реализуется только в вакууме, но на практике бывает, что
дисперсией можно пренебречь, например, при распространении света в воздухе;
2. ![]() . Показатель преломления убывает с
ростом длины волны. Такую дисперсию называют нормальной, и в этом
случае групповая скорость меньше фазовой. Такой тип дисперсии
типичен для прозрачных сред. Функция w = w(k), показанная на рис. 2.2,
соответствует нормальной дисперсии (см. задачу 4 к данному разделу).
. Показатель преломления убывает с
ростом длины волны. Такую дисперсию называют нормальной, и в этом
случае групповая скорость меньше фазовой. Такой тип дисперсии
типичен для прозрачных сред. Функция w = w(k), показанная на рис. 2.2,
соответствует нормальной дисперсии (см. задачу 4 к данному разделу).
3. ![]() . Показатель преломления растет с
ростом длины волны. Такая дисперсия называется аномальной, для
областей аномальной дисперсии характерно превышение групповой скорости
над фазовой и сильное поглощение света.
. Показатель преломления растет с
ростом длины волны. Такая дисперсия называется аномальной, для
областей аномальной дисперсии характерно превышение групповой скорости
над фазовой и сильное поглощение света.
 |
Отметим также, что идеально монохроматическая волна не переносит какой-либо информации, поэтому теория относительности не накладывает каких-либо ограничений на фазовую скорость, и возможны среды, в которых n < 1 и V > c.
Показатель преломления в среде может зависеть не только от частоты w, но и от волнового вектора k. Соответственно различают дисперсию временную n = n(w) и пространственную n = n(k). Последняя проявляется в виде анизотропии, т. е. зависимости свойств среды от направления. На языке фазовой и групповой скорости временная дисперсия означает отличие V от U по величине, а пространственная – по направлению.
Напомним некоторые важные соотношения между физическими
параметрами, характеризующими электрические свойства сред. Как известно, связь
между индукцией и напряженностью электрического
поля может быть записана двояко. Относительная диэлектрическая
проницаемость e показывает, во
сколько раз изменяется поле при попадании в среду: ![]() .
С другой стороны, поляризация среды: описывает аддитивную добавку
к внешнему полю:
.
С другой стороны, поляризация среды: описывает аддитивную добавку
к внешнему полю: ![]() . В приближении линейной
теории поляризация пропорциональна напряженности поля:
. В приближении линейной
теории поляризация пропорциональна напряженности поля: ![]() ,
где c – диэлектрическая восприимчивость.
Отсюда находим, что диэлектрическая проницаемость и поляризуемость связаны
соотношением
,
где c – диэлектрическая восприимчивость.
Отсюда находим, что диэлектрическая проницаемость и поляризуемость связаны
соотношением ![]() . В свою очередь диэлектрическая
проницаемость определяет показатель преломления среды: n2 = e. Таким образом, определив частотную
зависимость c(w), легко найти также зависимости e(w) и n(w),
т. е. закон дисперсии.
. В свою очередь диэлектрическая
проницаемость определяет показатель преломления среды: n2 = e. Таким образом, определив частотную
зависимость c(w), легко найти также зависимости e(w) и n(w),
т. е. закон дисперсии.
Отметим, что вектор поляризации среды P отстает по
фазе от внешнего поля световой волны Е, вследствие чего диэлектрическая
восприимчивость c(w), а, следовательно, и показатель
преломления n(w) являются
комплексными величинами. Очевидно, что комплексный показатель преломления ![]() не может трактоваться просто как
отношение скоростей света в вакууме и в среде. Для выяснения физического смысла
не может трактоваться просто как
отношение скоростей света в вакууме и в среде. Для выяснения физического смысла
![]() запишем уравнение монохроматической
световой волны, распространяющейся вдоль оси Z:
запишем уравнение монохроматической
световой волны, распространяющейся вдоль оси Z:
![]() , (2.3)
, (2.3)
Из (10) видно, что в среде с k ¹ 0 амплитуда поля убывает по мере проникновения света в глубь среды, т. е. происходит поглощение. Переходя от напряженности к интенсивности света, получаем:
![]() , (2.4)
, (2.4)
где коэффициент поглощения ![]() .
Соотношение (2.3) носит название закона Бугера-Ламберта-Бэра. Таким образом, действительная
часть комплексного показателя преломления определяет преломляющие (рефракционные)
свойства среды. Мнимая часть описывает поглощение
(абсорбционные свойства).
.
Соотношение (2.3) носит название закона Бугера-Ламберта-Бэра. Таким образом, действительная
часть комплексного показателя преломления определяет преломляющие (рефракционные)
свойства среды. Мнимая часть описывает поглощение
(абсорбционные свойства).
Обе части не являются независимыми: они связаны некоторыми общими интегральными соотношениями Крамерса-Кронига, что указывает на глубокую взаимосвязь казалось бы различных эффектов преломления и поглощения.
В квазиупругой модели атома движение электрона описывается уравнением, аналогичным (1.2) с той разницей, что в правой части присутствует вынуждающая сила, обусловленная падающей световой волной:
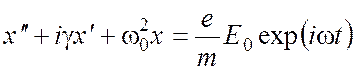 , (2.5)
, (2.5)
где e – заряд, m – масса электрона.
Стационарное решение этого уравнения имеет вид
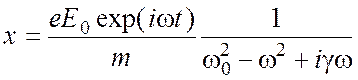 . (2.6)
. (2.6)
В результате смещения электрона из своего положения равновесия, атом
приобретает наведенный дипольный момент p = ex. Если среда
достаточно разряженная (взаимовлиянием поляризованных атомов друг на друга
можно пренебречь), то поляризация среды пропорциональна концентрации атомов N:
P = e0Np.
Следовательно, из (2.6) находим, что восприимчивость среды равна ![]() , где
, где ![]() –
плазменная частота, физический смысл которой подробно обсуждается в разделе
2.4. Таким образом, вещественная и мнимая части комплексной диэлектрической
проницаемости, описывающие дисперсию и поглощение света, оказываются равными
–
плазменная частота, физический смысл которой подробно обсуждается в разделе
2.4. Таким образом, вещественная и мнимая части комплексной диэлектрической
проницаемости, описывающие дисперсию и поглощение света, оказываются равными
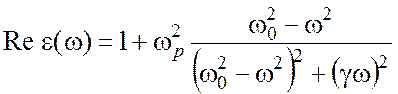 , (2.7)
, (2.7)
![]()
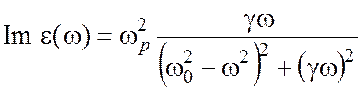 . (2.8)
. (2.8)
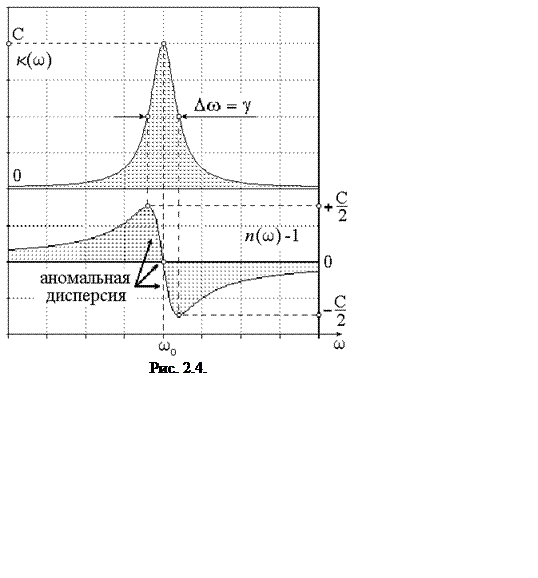
Анализ соотношений (2.7) и (2.8) упрощается, если
показатель преломления близок к 1, коэффициент поглощения мал, а частота света w близка к собственной частоте осциллятора w0, так что ![]() . Тогда
. Тогда
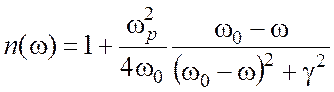 , (2.9)
, (2.9)
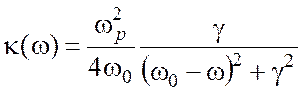 . (2.10)
. (2.10)
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.