Изучение классической теории дисперсии, страница 2

Экспериментально дисперсионную зависимость можно наблюдать с помощью метода скрещенных призм (рис. 2.5а). Первая призма (с вертикальным ребром) стеклянная, она разлагает проходящий через нее белый свет в спектральную полосу. Вторая призма (с горизонтальным ребром) изготавливается из исследуемого материала. Она смещает каждую точку спектра по вертикали, причем величина смещения зависит от показателя преломления на данной частоте. Таким образом, форма спектральной полосы на экране отражает зависимость показателя преломления от длины волны. На рисунке показан примерный вид спектра для случаев нормальной (НД) и аномальной (АД) дисперсии. Для более точного определения хода показателя преломления в области аномальной дисперсии, где велико поглощение, Д. С. Рождественским был предложен спектро-интерференционный метод "крюков", основанный на внесении дополнительной разности хода между опорным и измерительным пучками в двухлучевом интерферометре. В результате интерференционные полосы оказываются наклоненными, что позволяет количественно оценить параметры аномальной дисперсии (рис. 2.5б, дисперсия в парах натрия.).

1.4.  Дисперсия вдали от линий поглощения

Рассмотрим более подробно поведение показателя преломления прозрачных сред. При выполнении неравенства  дисперсионная формула (2.7) сводится к

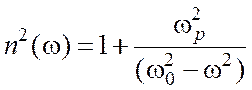.                                                (2.11)

При достаточно малой концентрации частиц N (газы) второе слагаемое в (2.11) мало и для показателя преломления получаем:

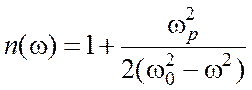.                                             (2.12)

Как следует из (2.12), при любых частотах в области прозрачности имеет место нормальная дисперсия (рис. 2.6). В реальных случаях собственные частоты w₀, как правило, лежат в ультрафиолетовом диапазоне. Поэтому для относительно низких частот (, видимая область) показатель преломления, как ему и 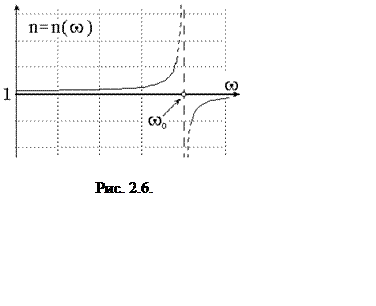положено, больше единицы. Напротив, в высокочастотной области (, рентгеновский диапазон) n < 1 и, следовательно, фазовая скорость волны больше скорости света в вакууме V > c. Как указывалось выше, это неравенство не противоречит теории относительности, поскольку монохроматическая волна является математической абстракцией. Из-за низкого показателя преломления в рентгеновской области может наблюдаться полное внутреннее отражение на переходе воздух – среда.

Предполагая, что w << w₀, дисперсионную формулу (2.11) можно разложить в ряд по степеням малого параметра w / w₀. Тогда

.

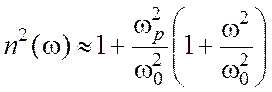Переходя от частоты к длине волны, получаем дисперсионную формулу Коши:

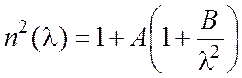,                                                 (2.13)

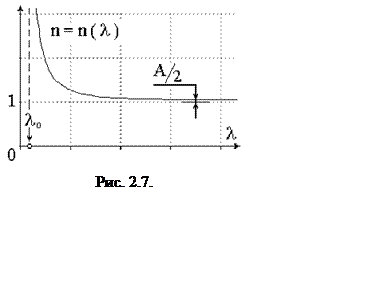
где  – коэффициент рефракции,  – коэффициент дисперсии (рис. 2.7). Несмотря на то, что формула Коши носит явно приближенный характер, она с удовлетворительной точностью описывает ход показателя преломления в области прозрачности. Так для водорода при нормальных условиях зависимость

n² = 1 + 2.72×10^-4 + (2.11×10^-6) / l²

оказывается справедлива для диапазона длин волн 0.4…9.0 мкм (для водорода l₀ » 90 нм).

Другой важный предельный случай дисперсии – w >> w₀. На практике он реализуется, например, при распространении электромагнитных волн в плазме, т. е. в среде, содержащей большое количество свободных зарядов, для которых вообще отсутствует квазиупругая сила (w₀ = 0). Из (2.11) в этом случае находим:

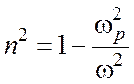.                                                                 (2.14)

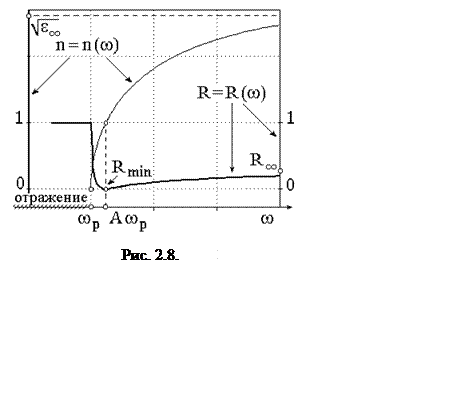Мало того, что показатель преломления меньше единицы, при w < w_p оказывается n² < 0, т. е. показатель преломления становится мнимым. Это означает, что при частотах излучения, меньших w_p, для любых углов падения наблюдается полное отражение (R = 1). Граничная частота 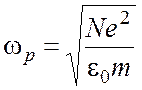 называется плазменной или лэнгмюровской частотой (рис. 2.8).

Описываемое явление проявляется, например, в отражении радиоволн от ионосферы. Концентрация заряженных частиц в ионосфере такова, что l_р лежит в области нескольких метров. Поэтому радиоволны коротковолнового диапазона с l > l_p отражаются от плазмы, обеспечивая дальнюю радиосвязь. Телевизионный же диапазон лежит по другую сторону плазменной частоты, поэтому прием телесигнала возможен только в зоне прямой видимости. В период магнитных бурь концентрация заряженных частиц резко возрастает, плазменная частота повышается, и складываются условия для сверхдальнего приема телевизионных передач метровых каналов.

Аналогично объясняется зеркальный блеск металлов, обусловленный плазмой свободных электронов.

Вблизи лэнгмюровской частоты наблюдается плазменный минимум отражения R_min, возникающий при переходе показателя преломления через 1.

Физический смысл плазменной частоты заключается в том, что это – частота собственных колебаний электронейтральной плазмы, состоящей из N частиц с зарядом ±e и массой m. Такие колебания могут возникнуть, например, при смещении заряженных частиц из положения равновесия. Тогда под действием кулоновских сил заряды противоположных знаков будут ускоренно двигаться навстречу друг другу, по инерции проскочат положение равновесия, затем начнут двигаться в обратном направлении и т. д.

Учтем теперь, что вклад в дисперсию дают колебания не только электронов, но и ионов. Поскольку масса ионов намного больше, соответствующие собственные частоты оказываются меньше. Ионные линии поглощения для веществ, прозрачных в видимой области, попадают в ИК-диапазон. Дисперсионная формула может быть записана в виде:

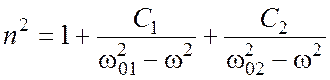.         (2.15)

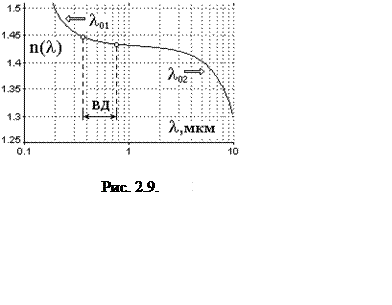
Например, для флюорита (CaF₂) длины волн, соответствующих электронным и ионным линиям поглощения равны соответственно l₀₁ = 0.094 мкм (УФ) и l₀₂ = 35 мкм (ИК) (рис. 2.9).

При переходе к очень низким частотам  основной вклад в показатель преломления дает именно ионная составляющая. Этим объясняется наблюдающееся у некоторых веществ кажущееся отличие измеряемой величины n от вычисленной по теории Максвелла: так для воды n = 1.33, а e = 81. Дело в том, что диэлектрическая проницаемость определяется для статического поля, а показатель преломления – в оптическом диапазоне. Между этими областями лежат инфракрасные ионные полосы поглощения.

Формулы (2.11), (2.15) были получены в предположении, что среда достаточно разреженная и взаимовлиянием поляризованных частиц можно пренебречь. В конденсированных средах (жидкости, твердые тела) локальное поле, действующее на рассматриваемый атом, обусловлено не только полем световой волны, но и соседними атомами. Г. Лоренц и Л. Лоренц показали, что в этом случае справедливо соотношение (формула Лоренц-Лоренца):

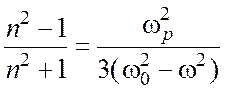.                                                    (2.16)

Если показатель преломления близок к единице, то n² + 1 » 3 и (2.16) переходит в (2.11). В правой части (2.16) величина пропорциональна концентрации атомов N, а, следовательно, и плотности вещества r. Поэтому во многих случаях справедлив закон постоянной удельной рефракции:

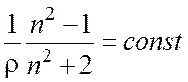.                                                         (2.17)

Например, для воздуха при увеличении давления в 200 раз удельная рефракция изменяется в пределах 10^-3.

Так же как и для классической теории излучения, классическая теория дисперсии требует уточнения с учетом квантовой природы вещества. Однако основные качественные (а во многих случаях и количественные) результаты остаются справедливыми. Так из квантовой теории следует, что дисперсионную формулу (2.11) следует заменить формулой Зельмейера

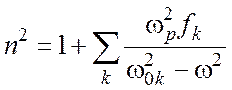,                                                   (2.18)

где  – частота, соответствующая одному из переходов между квантованными уровнями энергии атома, f_k – сила осциллятора, коэффициент, зависящий от квантовых чисел уровней.