



Отчёт по лабораторной работе №3
«Численные методы»
Вергентьева Тихона Юрьевича
2094/2
1. При интегрировании систем линейных уравнений на основе информации о значениях собственных чисел матрицы системы оценить максимальную величину шага устойчивого интегрирования и проверить эту оценку экспериментально.
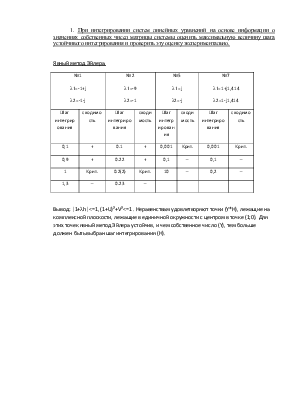
Явный метод Эйлера.
|
№1 l1=-1+j l2=-1-j |
№2 l1=-9 l2=-1 |
№5 l1=j l2=-j |
№7 l1=1+j1,414 l2=1-j1,414 |
||||
|
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
|
0,1 |
+ |
0.1 |
+ |
0,001 |
Крит. |
0,001 |
Крит. |
|
0,9 |
+ |
0.22 |
+ |
0,1 |
– |
0,1 |
– |
|
1 |
Крит. |
0.2(2) |
Крит. |
10 |
– |
0,2 |
– |
|
1,3 |
– |
0.23 |
– |
||||
Вывод: |1+lh|<=1, (1+U)²+V²<=1 . Неравенствам удовлетворяют точки (Y*H), лежащие на комплексной плоскости, лежащие в единичной окружности с центром в точке (1;0). Для этих точек явный метод Эйлера устойчив, и чем собственное число (Y), тем больше должен быть выбран шаг интегрирования (H).
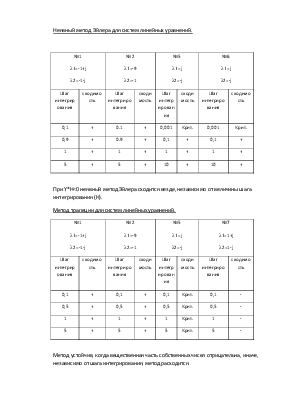
Неявный метод Эйлера для систем линейных уравнений.
|
№1 l1=-1+j l2=-1-j |
№2 l1=-9 l2=-1 |
№5 l1=j l2=-j |
№6 l1=j l2=-j |
||||
|
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
|
0,1 |
+ |
0.1 |
+ |
0,001 |
Крит. |
0,001 |
Крит. |
|
0,9 |
+ |
0.9 |
+ |
0,1 |
+ |
0,1 |
+ |
|
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
|
5 |
+ |
5 |
+ |
10 |
+ |
10 |
+ |
При Y*H<0 неявный метод Эйлера сходится везде, независимо от величины шага интегрирования (H).
Метод трапеции для систем линейных уравнений.
|
№1 l1=-1+j l2=-1-j |
№2 l1=-9 l2=-1 |
№5 l1=j l2=-j |
№7 l1=1+j l2=1-j |
||||
|
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
|
0,1 |
+ |
0,1 |
+ |
0,1 |
Крит. |
0,1 |
- |
|
0,5 |
+ |
0,5 |
+ |
0,5 |
Крит. |
0,5 |
- |
|
1 |
+ |
1 |
+ |
1 |
Крит. |
1 |
- |
|
5 |
+ |
5 |
+ |
5 |
Крит. |
5 |
- |
Метод устойчив, когда вещественная часть собственных чисел отрицательна, иначе, независимо от шага интегрирования, метод расходится.
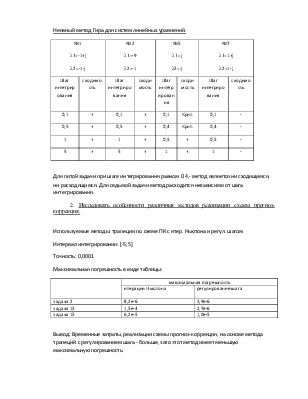
Неявный метод Гира для систем линейных уравнений.
|
№1 l1=-1+j l2=-1-j |
№2 l1=-9 l2=-1 |
№5 l1=j l2=-j |
№7 l1=1+j l2=1-j |
||||
|
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
Шаг интегрирования |
сходимость |
|
0,1 |
+ |
0,1 |
+ |
0,1 |
Крит. |
0,1 |
- |
|
0,5 |
+ |
0,5 |
+ |
0,4 |
Крит. |
0,4 |
- |
|
1 |
+ |
1 |
+ |
0,5 |
+ |
0,5 |
- |
|
5 |
+ |
5 |
+ |
1 |
+ |
1 |
- |
Для пятой задачи при шаге интегрирования равном 0.4,- метод является ни сходящимся, ни расходящимся. Для седьмой задачи метод расходится независимо от шага интегрирования.
2. Исследовать особенности различных методов реализации схемы прогноз-коррекция.
Используемые методы: трапеции по схеме ПК с итер. Ньютона и регул. шагом
Интервал интегрирования: [-5;5]
Точность: 0,0001
Максимальная погрешность в виде таблицы:
|
максимальная погрешность |
||
|
итерации Ньютона |
регулирование шага |
|
|
задача 2 |
8,2е-6 |
3,9е-6 |
|
задача 13 |
1,5е-4 |
2,7e-6 |
|
задача 15 |
6,2е-5 |
1,0e-5 |
Вывод: Временные затраты, реализации схемы прогноз-коррекция, на основе метода трапеций с регулированием шага - больше, зато этот метод имеет меньшую максимальную погрешность.
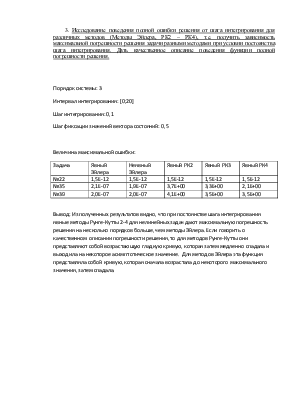
3. Исследование поведения полной ошибки решения от шага интегрирования для различных методов (Методы Эйлера, РК2 – РК4), т.е. получить зависимость максимальной погрешности решения задачи разными методами при условии постоянства шага интегрирования. Дать качественное описание поведения функции полной погрешности решения.
Порядок системы: 3
Интервал интегрирования: [0;20]
Шаг интегрирования: 0,1
Шаг фиксации значений вектора состояний: 0,5
Величина максимальной ошибки:
|
Задача |
Явный Эйлера |
Неявный Эйлера |
Явный РК2 |
Явный РК3 |
Явный РК4 |
|
№22 |
1,5E-12 |
1,5E-12 |
1,5E-12 |
1,5E-12 |
1,5E-12 |
|
№35 |
2,1E-07 |
1,9E-07 |
3,7E+00 |
3,3E+00 |
2,1E+00 |
|
№39 |
2,0E-07 |
2,0E-07 |
4,1E+00 |
3,5E+00 |
3,5E+00 |
Вывод: Из полученных результатов видно, что при постоянстве шага интегрирования явные методы Рунге-Кутты 2-4 для нелинейных задач дают максимальную погрешность решения на несколько порядков больше, чем методы Эйлера. Если говорить о качественном описании погрешности решения, то для методов Рунге-Кутты они представляют собой возрастающую гладкую кривую, которая затем медленно спадала и выходила на некоторое асимптотическое значение. Для методов Эйлера эта функция представляла собой кривую, которая сначала возрастала до некоторого максимального значения, затем спадала.
4. Сравнить оценки временных затрат при
интегрировании на [t![]() , t
, t![]() ] методами с регулированием шага и без регулирования. (сравнивать
следует методы одинакового порядка, например, РК4 и РКФ; трапеции, Гира).
] методами с регулированием шага и без регулирования. (сравнивать
следует методы одинакового порядка, например, РК4 и РКФ; трапеции, Гира).
Порядок системы: 3
Интервал интегрирования: [0;30]
Шаг интегрирования: 0,0001
Шаг фиксации значений вектора состояний: 0,5
Начальное состояние: 1,2,3
Время (в секундах):
|
Задача №25 |
Задача №28 |
Задача №32 |
|
|
Явный Эйлера |
4,056 |
4,061 |
3,035 |
|
РКФ |
0,052 |
0 |
0 |
|
Трапеции для линейных систем |
5,060 |
5,049 |
5,049 |
|
Трапеции с регулированием шага |
0 |
0,005 |
- |
|
Неявный Гира для линейных систем |
0 |
0 |
0 |
|
Неявный Гира с регулированным шагом |
0 |
0 |
- |
Вывод: Из результатов видно, что процесс интегрирования для методов с регулированным шагом, требуют меньше временных затрат, нежели методы с постоянным шагом. Неявный метод Гира производил интегрирование мгновенно для любого шага интегрирования.
5. При интегрировании жестких задач:
а) -получить экспериментальное подтверждение низкой эффективности (в смысле временных затрат) явных методов (методы РК4, РКФ)
Порядок системы: 3
Интервал интегрирования: [0;50]
Шаг интегрирования: 0,0001
Шаг фиксации значений вектора состояний: 0,5
Время (в секундах):
|
Задача №3 |
Задача №22 |
Задача №31 |
|
|
РК4 |
15 |
24 |
14 |
|
РКФ |
12 |
6 |
5 |
Вывод: При интегрировании жёстких задач, явные методы неэффективны, вплане временных затрат.
б) -установить возможность и условия интегрирования задачи неявными методами с большим и постоянным шагом; (метод трапеции)
Порядок системы: 3
Интервал интегрирования: [0;50]
Шаг фиксации значений вектора состояний: 0,5
|
Задача№2 (линейная) |
Задача№3 (жёсткая) |
Задача№13 (нелинейная) |
|
|
Шаг |
0,01 |
0,01 |
0,01 |
|
Погрешность |
3,0 |
Неуст. |
3,1 |
|
Шаг |
0,1 |
0.1 |
0,8 |
|
Погрешность |
2,7 |
Неуст. |
2,5 |
|
Шаг |
0,5 |
0,5 |
1,0 |
|
Погрешность |
Неуст. |
Неуст. |
Неуст. |
Вывод: Исследование, проведенное для установления возможности и условия интегрирования для жестких задач с большим и постоянным шагом, показывает, что для неявных методов условие устойчивости сохраняется до тех пор, пока величина λ*h принадлежит области его абсолютной устойчивости.
в) -сравнить эффективность применения метода Гира второго порядка с методом трапеции
Порядок системы: 3
Интервал интегрирования: [0;50]
Шаг интегрирования: 0,1
Шаг фиксации значений вектора состояний: 0,5
Начальное состояние: 1,2,3
Максимальная погрешность:
|
Метод Гира |
Метод трапеций |
|
|
Задача №3 |
20 |
5,3 |
|
Задача №12 |
5,9 |
5,9 |
|
Задача №22 |
18 |
8,5 |
|
Задача №31 |
3,7 |
0,45 |
Вывод: Из полученных результатов видно, что эффективность применения метода трапеций выше, нежели метод Гира 2 порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.