Коэффициенты квадратичного уравнения. Величина «звездного» плеча "a" и параметр "а". Проверка однородности построчных дисперсий при одинаковом числе

Курсовая  работа  по дисциплине "Исследование и планирование эксперимента в СЭС" для студентов заочной формы обучения

Задание:

Для условно однородной сети 10 кВ получить регрессионную зависимость потерь активной мощности (DP) от величины входной мощности (Р_A).

Исходные данные:

Расчетная схема (по вариантам : а, б, в) приведена на рис. 1, а исходные данные по вариантам  задания - в табл. 1.

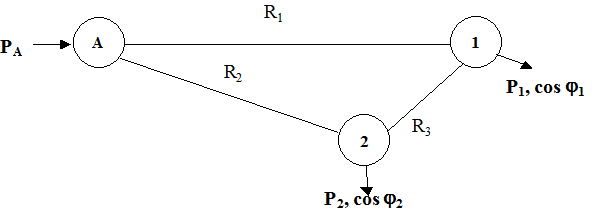         а) замкнутая схема («треугольник»)

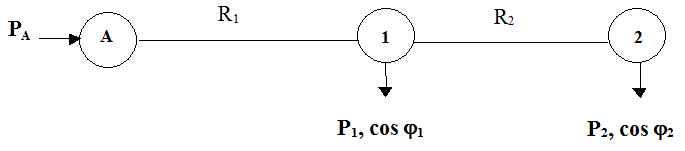
б) радиальная схема

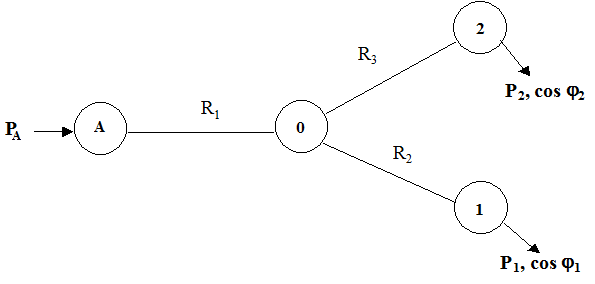
в)  схема в виде «звезды»

Рис.1. Расчетная схема (по вариантам: а, б, в )

Примечание: принять, что значения "Р" нагрузок узлов 1 и 2 лежат в диапазоне

(0,4 - 0,6)ЧP_A, а коэффициенты мощности ( cos j₁ и cos j₂) изменяются в пределах

0,8 - 0,95.

Таблица 1

Исходные данные по вариантам задания

Методические указания :

если считать, что Р1 = P_AЧK, тогда P2 =  P_A×(1-K) , где  0,4  Ј  K  Ј  0,6.       При условии cos j1= cos j2 переток мощности S_{i j} в произвольной ветви i-j схемы Чравен S_{i j}=P_AЧ(C_{i j}+Cў_{i j}K), где константы С_{i j}, и Cў_{i j} определяются значениями cos j и сопротивлениями ветвей. Если cos j₁№ cos j₂, то зависимости S_{i j} будут качественно теми же, хотя и более громоздкими. Потери активной мощности в ветви i-j определяются как DP_{i j}=(S_{i j}/U_ном)²ЧR_{i j}. Сказанное позволяет предположить, что  DP@P²_AЧ(b₀+b₁K+b₂K²),                                                           (1)

где b₀, b₁, b₂ - коэффициенты квадратичного уравнения.

Покажем это на примере радиальной схемы (вариант б) ). Пусть cos j1=

=cos j2=1. Если Р1 = P_AЧK и P2 =  P_A×(1-K),  то потоки мощностей по ветвям схемы будут Р₁₂= P_A×(1-K), Р_А1=Р_А. Потери активной мощности определятся как

.

Отсюда получаем, что     .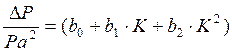

Из этого следует, что вначале можно получить уравнение регрессии вида

y = DP/P²_A = b₀+b₁K+b₂K², а затем перейти к модели (1). Тогда основная задача - построить квадратичную однофакторную модель y = b₀+b₁K+b₂K², например, на основе ОЦКП [1].

“Имитационные” опыты (расчеты) выполняют в следующем порядке.

1)  Задают Р_A (не важно какую, но одинаковую во всех опытах, например, равную значению в середине диапазона Р_А) и коэффициенты мощности (cos j1, cos j2 ) в различных сочетаниях, т.е.:  (0,8; 0,8), (0,8; 0,95), (0,95; 0,8), (0,95; 0,95). Таким образом, cosj1=(0,8; 0,8; 0,95; 0,95), а cosj2=(0,8; 0,95; 0,8; 0,95).

2)  В соответствии с планом эксперимента и кодированным значением х_j (табл. 2) определяют значение K_j в натуральных единицах, т.е. K_j=K₀+x_j×DK; (j=1,2, …,5)

3)  Находят сначала активные нагрузки узлов для j-го опыта:  Р1_j = P_A× K_j;  Р2_j = (1- K_j )×P_A ; а затем реактивные нагрузки узлов в соответствии с принятыми cos j1 и cos j2,  т.е.: 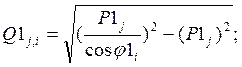 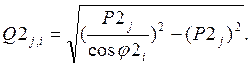(i=1,2,3,4). Далее определяют потоки мощностей по ветвям схемы  и вычисляют суммарные потери активной мощности (DР) для всей сети,  которые затем делят на Р_A ², т.е. находят y_{j k}=DР / Р_A ² (k=1..n). "Дублирующие" опыты (n=4) проводят в том же порядке, но для разных сочетаний cos j1 и cos j2 (см. п. 1). Заметим, что расчет DР для разных сочетаний cos j1 , cos j2 позволяет неявно учесть в регрессионной модели составляющую потерь от реактивной нагрузки.