Коэффициенты квадратичного уравнения. Величина «звездного» плеча "a" и параметр "а". Проверка однородности построчных дисперсий при одинаковом числе, страница 2

Все расчеты удобно оформлять в табличном виде, например, как это показано в  табл. 2.

Таблица 2

Информационная таблица

Величина «звездного» плеча "a" и параметр "а" определяются по формулам:

;  ;  где k = 1 -число факторов,

N = 2^k + 2Чk + 1 = 2¹ + 2Ч1 + 1 = 5  - общее число опытов.

Значение фактора K в натуральных единицах меняется в пределах  0,4 Ј K Ј 0,6. Вычислим основной (нулевой) уровень:  K₀=(K _max+K_min)/2=(0,6+0,4)/2=0,5 и диапазон DK=(K_max-K_min)/2=(0,6-0,4)/2=0,1. Кодированное значение фактора определяется как х=(K-K₀)/ DK. Например, для нижнего значения фактора равного K_min=0,4, кодированное значение будет х_min=(K-K₀)/ DK=(0,4-0,5)/0,1=-1. Cледовательно,  кодированное значение фактора х_max = +1, соответствует верхнему значению фактора в натуральных единицах K_max=0,6, а х=0 соответствует K₀=0,5.  Значение фактора  К для j-го опыта в зависимости от величины х_j определяют по формуле  K_j = K₀ + x_j·DK = 0,5 + x_j·0,1 .

Для каждой строки матрицы планирования эксперимента можно найти построчные дисперсии, которые характеризуют ошибку j–го опыта : 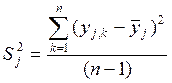,  где 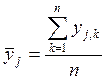 ,  (n=4).

Проверка однородности построчных дисперсий при одинаковом числе

дублирующих опытов выполняется по критерию Кохрена: 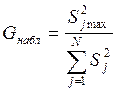,  а G_кр=G_{0.05,n-1, N(n-1)} определяется по таблицам, например в  [3]. Если G_набл<G_кр, то гипотеза об однородности дисперсий принимается.

То же самое можно выполнить и по критерию Фишер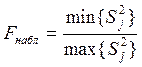а: ,  а

F_кр=F_{0.05,n1, ,n2} , где n1 = n-1 = 3, n2 = n-1 = 3 – число степеней свободы для числителя и знаменателя в формуле для  , также можно найти по таблицам [3]. Если F_набл<F_кр, то гипотеза об однородности дисперсий принимается.