Коэффициенты квадратичного уравнения. Величина «звездного» плеча "a" и параметр "а". Проверка однородности построчных дисперсий при одинаковом числе, страница 3

После этого вычисляется дисперсия ошибки всего эксперимента:   .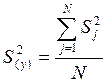

Коэффициенты уравнения регрессии  y  = DP/P²_A = bў_o+b₁x+b₂(x² - a) вычисляют обычным способом, т.е. или в матричном виде B=(x^T×x)^-1 ×x^T×Y_cp , или по простым формулам : 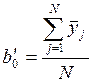,  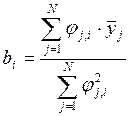;  где  i=1, 2;  j_j,i- j-й элемент i-го столбца матрицы плана эксперимента ( см. информац. табл. 2).

Поскольку уравнением регрессии вида y  = DP/P²_A = bў_o+b₁x+b₂(x² - a) пользоваться неудобно, то коэффициент bў_o пересчитывают по формуле

b_o= bў_o- aЧb₂  и уравнение регрессии приобретает вид y = DP/P²_A = b_o+b₁x+b₂x² , или y = DP = P²_A ×(b_o+b₁x+b₂x²). Кодированные значения "x" изменяются в пределах от –1 до +1.

Оценки дисперсий коэффициентов b_i (i = 0,1,2) уравнения регрессии можно найти как в матричном виде для общего случая, т. е. D = (x^T×p×x)^-1×S²_(y) , где р – диагональная матрица с числом дублирующих опытов (в ней на месте диагональных элементов стоят значения n (для нашего случая n=4), а остальные элементы равные нулю), так и в более простом виде для ортогональной матрицы  планирования (в нашем случае именно такая матрица), например, оценка дисперсии коэффициента b_oў найдется как: 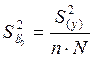 , а оценки дисперсии остальных коэффициентов: 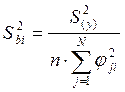, i=1, 2   (n=4 – число дублир. опытов).

Для пересчитанного коэффициента b_o оценка его дисперсии равна

S² _bo = S² _boў + a²Ч S² _b2.

Проверка значимости коэффициентов уравнения регрессии выполняется по условию  | b_i | і t_крЧS_bi, где  t_кр=t_{0.05, N(n-1)}=t_0.05,15 определяется по таблицам Стьюдента [4], а    - средние квадратичные ошибки коэффициентов b_i.

Для перехода от уравнения регрессии  y = DP = P²_A ×(b_o+b₁x+b₂x²) в кодированных значениях "x"  к уравнению y = DP = P²_A ×(b_o+b₁K+b₂K²) в натуральных значениях "K" достаточно заменить  в уравнении регрессии "x" на

x=(K-K_o)/ DK=(K-0,5)/0,1 . Здесь уже значения "K" изменяются в пределах  от 0,4 до 0,6.

Для наглядности можно построить зависимости   DP = f(K, P_A), например, для трех значений  K=0,4; K=0,5; K=0,6  и  Ра, изменяющуюся  в диапазоне от   Ра_мин до Ра_макс (из табл. 1). ).  Для случая, когда получается значимым только один коэффициент b₀ и уравнение регрессии приобретает вид  DP = P²_A ×b₀ , эта зависимость уже не зависит от "K" и получается только одна кривая. 

Примечание:записка к курсовому проекту кроме вычислительной части должна содержать и текстовую часть, в которой должен быть как теоретический материал, так и пояснения ко всем вычислениям. Особенно это относится к случаю, если проект выполняется с использованием математических пакетов MathCad, MathLab  и им подобных.

Литература

1.  Ф.Г. Гусейнов, О.С. Мамедяров. Планирование эксперимента в задачах электроэнергетики. -М.:  Энергоатомиздат, 1988. -151 с.

2.  Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. Планирование эксперимента при поиске оптимальных условий. -М.:. «Наука», 1978. -279 с. 

3.  Гмурман В. Е. Руководство к  решению задач по теории вероятностей и математической статистике.  -М.:  «Высш. школа», 1979. -400 с.