Теория телефонных сообщений. Потоки вызовов, нагрузка показатели качества обслуживания. Теория телефонных сообщений. Потоки вызовов, нагрузка показатели качества обслуживания, страница 6

 - эмпирический коэффициент, зависящий от средней длительности интервала между повторными вызовами S, вероятности потерь р и первичной поступающей нагрузки У_перв.

Далее число линий в пучке рассчитывает по известным формулам для модели простейшего потока вызова, в которые вместо поступающей нагрузки У подставляют значения приведённой нагрузки Z.

Второй учебный вопрос

Неполнодоступный неблокируемый пучок

Такие пучки относятся к тем системам распределения информации, аналитический расчет которых достаточно сложен.

Разработана несколько приближённых методов расчёта:

Формула Пальма – Якобеуса

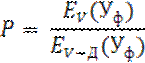
где У_ф – фиктивная нагрузка

У_ф = [1 - E_V(У_ф)] / (1- р) = У_р

В тех случаях когда требуется определить число линий в пучке с заданной фиксированной доступностью D удобно пользоваться формулой  основанной на теореме О`Дела. В соответствии с этой теорией следует, что нагрузка обслуживающаяся неполнодоступным пучком емкостью V определяется как сумма нагрузок обслуженных полнодоступных пучков содержащих D – линий и неполнодоступным пучком из V – D линий при условии, что все пучки работают при одной и той же вероятности Р. При фиксированных значениях D и р формула имеет вид линейной зависимости

 – коэффициенты, зависящие от доступности D и вероятности потерь р.

Значение этих коэффициентов табулировано.

Третий учебный вопрос

Блокируемые полнодоступные и неполнодоступные пучки

Расчёт числа линий при звеньевом включении производится с помощью формул, учитывающих потери, обусловленные отсутствием не только свободных линий, но так же внутренней структуры блока коммутации.

Задача расчета вероятности потерь в блокируемых пучках чаще всего связана  с коммутационными полями станций квазиэлектронной системы, хотя в цифровых АТС нередко встречаются многозвенные структуры, низкая стоимость электро коммутационных элементов позволяет конструировать оборудование с таки расчетом чтобы вероятность была мала. Приближенным методом расчета полнодоступных блокируемых пучков является метод Якобеуса.

Параметр двухзвенного блока работает в режиме группового искания (рис.8.1.2):

Рис.8.1.2. Двухзвенная ступень искания

К – число коммутаторов звена А; m и n – число входов и выходов коммутатора звена А; g – число выходов направлении каждого коммутатора звена В; n1 – число направлений связи, линий которых включаются в выходы звена В;

f – связность блока (число промежуточных линий) между каждым коммутатором звена А и В;

Расчёт звеньевых включений может быть произведён методом Якобеуса.

Для полнодоступных блокируемых пучков группового искания расчётная нагрузка У_р и число линий пучка V = mg определяется по формуле

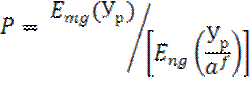
где У_р – расчётная величина нагрузки, поступающая от направления связи а – расчётная нагрузка, приходящаяся на один вход рассматриваемого блока

m,n,g,f – параметры блока

В числителе и знаменателе E означает величину потерь, определённую по формуле Эрланга для полнодоступного пучка, содержащего соответственно mg и ng линий.

Если в направлении число линий пучка V < m, то расчёт потерь по этой формуле производится при g = V/m. Полученное в результате число значение р сравнивается с заданной нормой потерь. При несоответствии этих величин расчёт повторяется при другом выбранном в направлении числе линий.

Если при звеньевом включении расчётная величина поступающей нагрузки в направлении превышает пропускную способность полнодоступного пучка в mg линий, то для повышения их использования при помощи неполнодоступного включений образуют пучки, содержащие число линий V > mg. При этом число линий не полнодоступного блокируемого пучка может быть определена при помощи формулы, предложенной ЛОНИИС

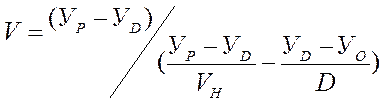
Где У_р – расчётная величина нагрузки, поступающая на рассматриваемый пучок линий

У_D – нагрузка, поступающая к полнодоступному неблокируемому пучку, содержащему D = mg, при условии, что потери равны заданной величине р.

У₀ – нагрузка поступающая через коммутационный блок к блокируемому полнодоступному пучку с Д = mg линий при условии, что потери равны р.

V_H – число линий неполнодоступного неблокируемого пучка при D = mg и допустимой величине потерь р.