2. Дисциплина без преоритетов при которой ни один из поступивших вызовов не имеет преимуществ перед другими (телефонная сеть общего пользования).
Функционирование систем с разными дисциплинами обслуживания характеризуется различными показателями.
В системах с потерями основным показателем качества обслуживания является вероятность потерь по вызовам (Р), равная математическому ожиданию отношения числа потерянных вызовов (Сп) к общему числу поступивших (С).
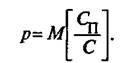
Иногда рассчитывают вероятность потерь по нагрузке и по времени

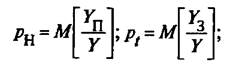
Yп – потерянная нагрузка
Y – поступающая нагрузка
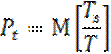
Тз – сумма длительности, в течении которой наблюдается занятость всех обслуживаемых устройств
Т – общее время наблюдения.
Для систем с ожиданием показателем качества обслуживания являются функция распределения длительности ожидания и среднее время ожидания.
Распределение длительностей ожидания характеризуется вероятностью Р>t того, что поступивший вызов будет обслужен после некоторого времени
ожидания ![]() ,
превышающие заданное значение t.
,
превышающие заданное значение t.
Функция распределения длительности ожидания даёт исчерпывающую информацию в качестве обслуживания. Однако в инженерных расчётах удобны дискретные характеристики: вероятность ожидания, средняя длительность ожидания.
Р>0 представляет значение функции Р>t при t = 0. Это вероятность задержки обслуживания вызова на время t > 0.
Средняя длительность ожидания характеризует время, на которое задерживается обслуживание вызовов. Различают:
- Средняя длительность ожидания для всех поступивших вызовов j.
- и только для тех вызовов обслуживание которых было задержано jож.
Качество обслуживания в комбинированных системах оцениваются показателями, свойственными системам с потерями и системам с ожиданием – вероятностями потерь, вероятностями ожидания и средняя длительность занятия..
Лекция 3
Расчет полнодоступных и неполнодоступных пучков
ВОПРОСЫ :
1. Полнодоступный неблокируемый пучок.
2. Неполнодоступный неблокируемый пучок.
3. Блокируемые полнодоступные и неполнодоступные пучки
Первый учебный вопрос
Полнодоступный неблокируемый пучок
Полнодоступный неблокируемый пучок часто встречается в практических задачах. Рассмотрим основные математические модели, которые используются для описания элементов сетей связи с потерями вызовов.
Для системы М|М|V|L (простейший поток вызовов, экспоненциальное распределения длительности обслуживания, пучок содержит произвольное число линий, система обслуживается с потерями), в случае простейшего потока зависимость потока между вероятность потерь, поступающей нагрузкой и числом линий пучком определяется по 1 – ой формуле Эрланга.
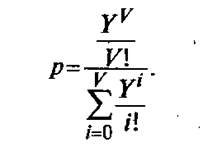
Где Yр – расчётная величина телефонной нагрузки, поступающей на приборы пучка
V – число приборов, линий
i – число занятых линий пучка
Существует упрощённая форма записи
![]()
Так как непосредственное вычисление величины Еv(Y) затруднительно, то обычно используют графики (рис.8.1.1) или таблицы.
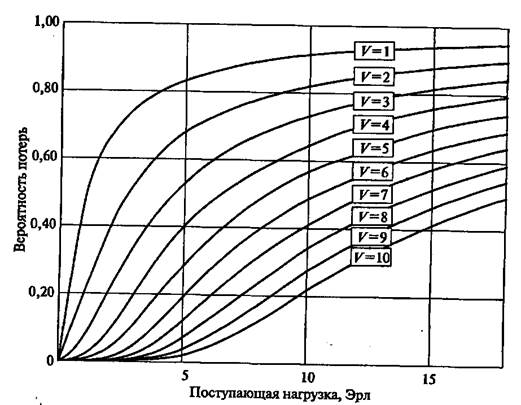
Рис.8.1.1. Графики вероятности потерь в системе М|М|V|L
Для системы G|M|V|L (G-поток имеет случайный характер…) и примитивного потока вызовов существует аналитическое решение: вероятности потерь по вызову, по времени и по нагрузке имеют различные значения. Эти формулы называются формулы Энгсета
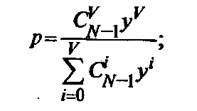
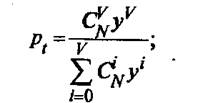
![]()
Где ![]() - число
сочетаний из N по V
- число
сочетаний из N по V
N – число источников вызовов
y = ![]() –
нагрузка, поступающая от одного источника, в момент, когда он свободен.
–
нагрузка, поступающая от одного источника, в момент, когда он свободен.
Математическую модель примитивного потока вызовов используют при ограниченном числе источников вызовов (когда N < 15V). При N → ∞ формулы Энгсета переходят в первую формулу Эрланга.
Для систем G|M|V|L и потока с повторными вызовами аналитическое решение затруднено тем, что число источников повторных вызовов неограниченно и может изменяться от 0 до бесконечности. Существует ряд приближенных методов расчёта для систем с повторными вызовами. Этот метод предложен С.Л. Дюфуром, используется для проектирования пучков междугородних линий сети телефонной связи ж.д. транспорта. Для учёта эффекта повторных попыток вычисляется так называемая приведённая поступающая нагрузка
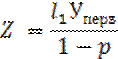
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.