Портфель ценных бумаг. Динамика (временной ряд) годовых доходностей по акциям заданных конкретных фирм, страница 2

[e2] 

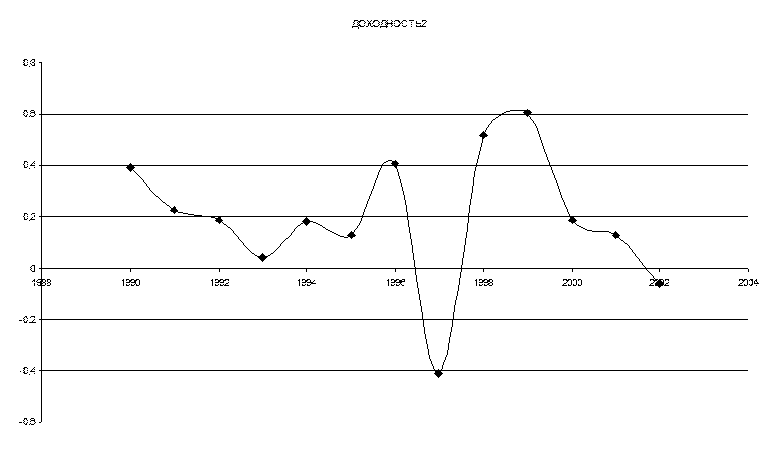
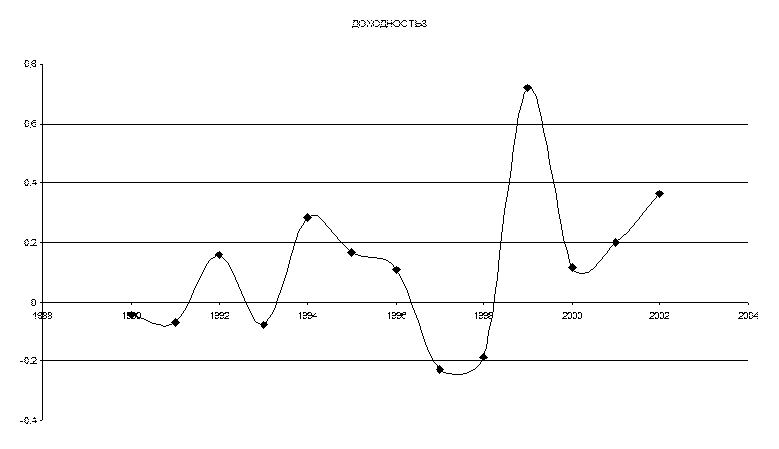
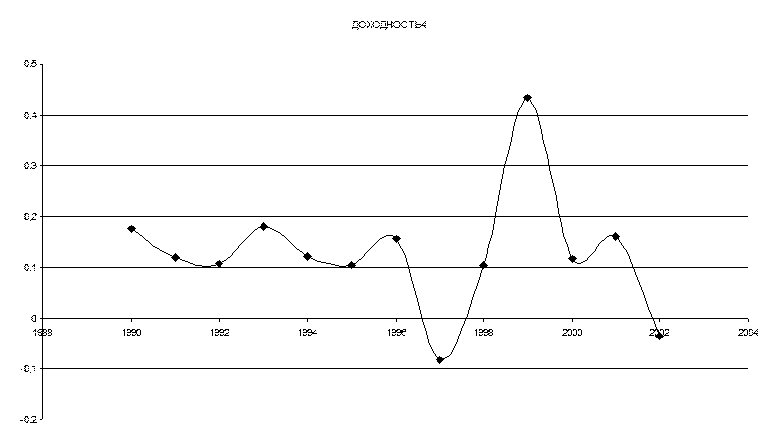
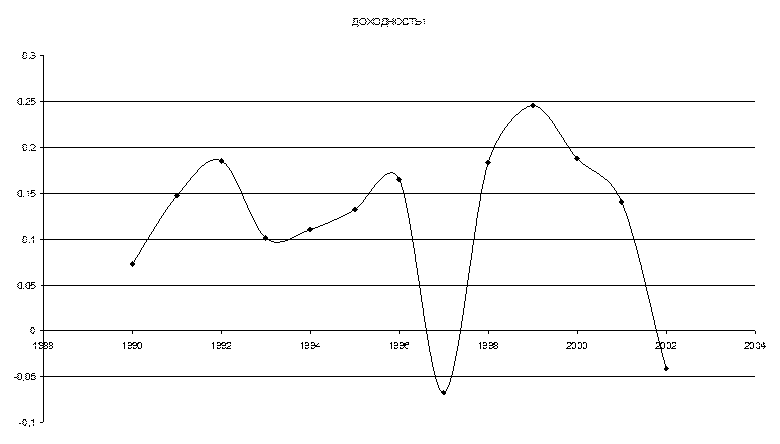
2. Средняя доходность каждого вида акции вычисляется по формуле

, , .

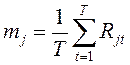Получим

Элементы ковариационной матрицы находятся как

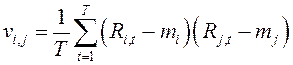
ковариационная матрица
	1	2	3	4
1	0,096901091
2	0,01756052[e5]	0.063343174
3	0,00689192	0.021004461	0.059234
4	0,00760311	0.022625121	0.015834	0.013286308

3. Вычислить математическое ожидание и дисперсию годовой доходности всего рынка.

Средняя доходность по всему рынку ценных бумаг при условии, что число бумаг каждого вида равно 1 вычисляется

,  .

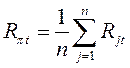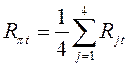Получим

	средняя доходность ()
1990	0,149393768[e6]
1991	0,106420638
1992	0,159982217
1993	0,060697553
1994	0,174511408
1995	0,132314205
1996	0,209079375
1997	-0,196440796
1998	0,155242703
1999	0,50115133
2000	0,153169255
2001	0,158373596
2002	0,057462176

Математическое ожидание доходности всего рынка

, .

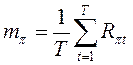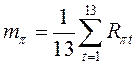Дисперсия доходности всего рынка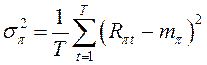

средняя доходность
Среднее	0,14010442[e7]
Дисперсия выборки	0,02039265[e8]

4. Построить параметрическую модель рынка ценных бумаг и найти коэффициенты «альфа» и «бета» для каждого вида акций.

Ковариационные моменты всего рынка и доходности -ой акции определим как . Получим

Тогда искомые коэффициенты

,[e10] 

[e11] .

0,518520	1,58720	1,208253	0,7275768[e12]

альфа
	0,0476029
	-0,0669586
	-0,0528316
	0,0263895[e13]

Вывод.

Для первого и четвертого вида акций коэффициент альфа положителен. Это значит, что темпы роста их курса за рассматриваемый период выше, чем в среднем по рынку. И наоборот, для второго и третьего вида акций темпы роста их курса за рассматриваемый период ниже чем в среднем по рынку. 

Для первого и четвертого вида акций бета-коэффициент меньше единицы. Значит, эти акции менее рискованны, чем в среднем на рынке. Для второго и третьего вида акций бета-коэффициент больше единицы. Значит, эти акции более рискованны, чем в среднем на рынке

Второе задание:

По результатам статистической обработки временных рядов цен и дивидендов акций четырех фирм, выполненных ранее, исследовать структуру оптимального инвестиционного портфеля акций в зависимости от задаваемой доходности портфеля.

1. Построить зависимость рационального риска (минимум среднеквадратического отклонения доходности) портфеля от желаемой доходности портфеля (например, 6%, 8%, 10%, 11%, 15%, 18%).[e14]