|
1) 0,51%; |
2) 0,38%; |
3) 0,54%; |
4) 0,63%; |
5) 0,75%. |
18. Определите максимальную доходность портфеля модели Блэка ![]() для двух
активов
для двух
активов ![]() и
и ![]() с
доходностями
с
доходностями ![]() и
и ![]() при
при ![]() .
.
|
1) 1; |
2) 0; |
3) |
4) |
5) -1. |
19. Определите максимальную доходность портфеля модели Блэка ![]() для двух
активов
для двух
активов ![]() и
и ![]() с
доходностями
с
доходностями ![]() и
и ![]() при
при ![]() .
.
|
1) 1; |
2) 0; |
3) |
4) |
5) -1. |
20. Определите максимальную доходность портфеля модели Блэка ![]() для двух
активов
для двух
активов ![]() и
и ![]() с
доходностями
с
доходностями ![]() и
и ![]() при
при ![]() .
.
|
1) 1; |
2) 0; |
3) |
4) |
5) -1. |
21. Портфель ценных бумаг – это:
1) две и более ценные бумаги;
2) два и более ценных актива;
3) объединение двух и более векселей;
4) объединение двух и более ценных бумаг и активов;
5) объединение наиболее выгодных ценных бумаг и активов.
22. Стандартный портфель подразумевает:
1) равные доли ценных бумаг и активов;
2) наличие только ценных бумаг;
3) неотрицательные равные доли всех активов;
4) неотрицательность всех долей активов;
5) положительные доли всех активов.
23. Если Si(0) – начальная цена единицы актива Ai , то инвестируемый в портфель капитал определяется как:
1) 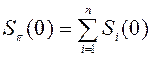 ; 2)
; 2) 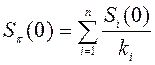 ; 3)
; 3)
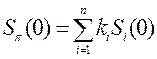 ;
;
4) 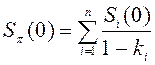 ; 5)
; 5) 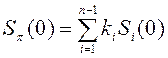 .
.
24. Относительный «вес» xi каждого актива в портфеле определяется как:
1) 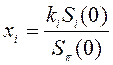 ;2)
;2)
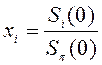 ; 3)
; 3) 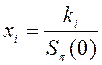 ; 4)
; 4) 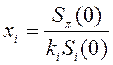 ; 5)
; 5) 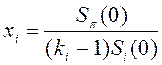 .
.
25. Доходность портфеля ![]() ценных
бумаг за период Т вычисляется по формуле:
ценных
бумаг за период Т вычисляется по формуле:
1) 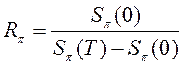 ; 2)
; 2) 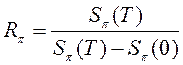 ; 3)
; 3) 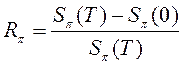 ;
;
4) 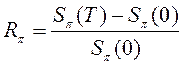 ;5)
;5)
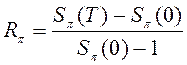 .
.
26. Бета i-го вклада относительно оптимального портфеля определяется формулой:
1)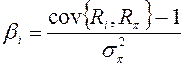 ; 2)
; 2)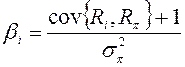 ; 3)
; 3)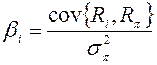 ;
;
4) 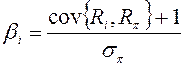 ; 5)
; 5) 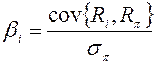 .
.
27. При оптимизации портфеля ценных бумаг выделяют основной подход к получению структуры портфеля:
1) максимальная доходность при заданной инвестором величине риска конечного портфеля;
2) минимальная величина риска при заданной инвестором доходности конечного портфеля;
3) максимальная доходность;
4) максимальная доходность и минимальная величина риска при заданной инвестором величине риска конечного портфеля;
5) минимальная величина риска.
28. Что является особенностью модели Марковица:
1) ограниченность доходности портфелей;
2) неограниченность доходности портфелей;
3) доходность любого стандартного портфеля превышает наибольшую доходность активов, из которых он построен;
4) максимальная доходность портфеля;
5) минимальный риск портфеля.
29. В модели Тобина-Шарпа-Литнера предполагается:
1) существование безрискового актива, доходность которого прямо пропорционально зависит от состояния рынка и имеет постоянное значение;
2) существование безрискового актива, доходность которого не зависит от состояния рынка и имеет переменное значение;
3) существование безрискового актива, доходность которого не зависит от состояния рынка и имеет постоянное значение;
4) существование безрискового актива, доходность которого зависит от состояния рынка и имеет переменное значение;
5) существование безрискового актива, доходность которого зависит от состояния рынка и имеет постоянное значение.
30. В модели Блэка допустимыми являются любые портфели, удовлетворяющие основному ограничению:
1) 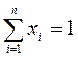 ; 2)
; 2) 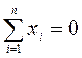 ; 3)
; 3) 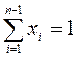 ; 4)
; 4) 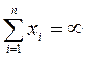 ; 5)
; 5) 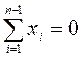 .
.
31. Каким уравнением изображается класс допустимых уравнений в модели Блэка для рынка из двух активов:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
32. Параметрическая модель рынка ценных бумаг определяется:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.