ЭДС ИНДУКЦИИ
Электромагнитная индукция: в замкнутом проводящем контуре при изменении магнитного потока (т.е. вектора B! ), охватываемого этим контуром, возникает электрический ток индукционный ток.
Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине его вызывающей.
Закон электромагнитной индукции: εi = − ddtΦ возникающая в контуре
ЭДС индукции.
![]() Если замкнутый
контур, в котором индуцируется ЭДС состоит не из одного витка, а из N витков и, если, магнитный
поток, охватываемый каждым витком одинаков и равен Φ1, то суммарный поток Φ
сквозь поверхность, натянутую на данный контур: Φ = NΦ1 полный магнитный поток
или потокосцепление. εi = −N ddtΦ1 .
Если замкнутый
контур, в котором индуцируется ЭДС состоит не из одного витка, а из N витков и, если, магнитный
поток, охватываемый каждым витком одинаков и равен Φ1, то суммарный поток Φ
сквозь поверхность, натянутую на данный контур: Φ = NΦ1 полный магнитный поток
или потокосцепление. εi = −N ddtΦ1 .
Изменение тока в контуре, которое ведет к возникновению ЭДС индукции в этом же контуре называется самоиндукцией.
Если в пространстве, где находится контур с током I , нет ферромагнетиков, то полный магнитный поток через контур пропорционален силе тока I : Φ = LI , где L коэффициент пропорциональности индуктивность контура.
Взаимная индукция:
Рассмотрим два неподвижных контура 1 и 2, расположенных достаточно близко друг к другу. Если в контуре 1 течет ток I1, то он создает через контур 2 полный магнитный поток Φ2, пропорциональный (при отсутствии ферромагнетиков) току I1: Φ =2 L I21 1.
Аналогично, если в контуре 2 течет ток I2, он создает через контур 1 полный магнитный поток: Φ =1 L I12 2.
Коэффициенты L12 и L21 называют взаимной индуктивностью контуров.
Теорема взаимности: при отсутствии ферромагнетиков коэффициенты L12 и L21 одинаковы: L12 = L21.
Взаимная индукция: при всяком изменении тока в одном из контуров в другом контуре возникает ЭДС индукции.
Согласно закону электромагнитной индукции, ЭДС, возникающие в контурах 1 и 2 равны, соответственно: ε1 = − ddtΦ1 = −L12 dIdt2 ,
![]() ε2 = − ddtΦ = −L21 dIdt1 .
ε2 = − ddtΦ = −L21 dIdt1 .
С учетом явления электромагнитной индукции, закон Ома для контура 1:
![]() R I1 1 =ε1 −
L1 dIdt1 −
L12 dIdt2 , где ε1 сторонняя ЭДС в контуре
1 (помимо индукционных ЭДС), L1 индуктивность контура
1.
R I1 1 =ε1 −
L1 dIdt1 −
L12 dIdt2 , где ε1 сторонняя ЭДС в контуре
1 (помимо индукционных ЭДС), L1 индуктивность контура
1.
Энергия магнитного поля:
Дополнительная работа, совершаемая сторонними силами против ЭДС самоиндукции в процессе установления тока: δAдоп = IdΦ .
При отсутствии ферромагнетиков контур с индуктивностью
L, по которому течет
ток I обладает энергией:
W =
12 LI2 =
12 IΦ = ![]() Φ2L2 магнитная
Φ2L2 магнитная
![]()
W ![]() dV энергия магнитного поля.
dV энергия магнитного поля.
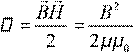 объемная плотность
магнитной энергии. Данное выражение справедливо лишь для случаев, когда
зависимость B H! !(
) линейная, т.е. для пара- и диамагнетиков.
объемная плотность
магнитной энергии. Данное выражение справедливо лишь для случаев, когда
зависимость B H! !(
) линейная, т.е. для пара- и диамагнетиков.
W = L I1 12 2 + L I2 22 2 + L I I12 1 2 магнитная энергия двух контуров с токами; первые два слагаемых собственная энергия, последнее слагаемое взаимная энергия.
W 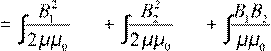 dV dV dV полевая трактовка энергии, где B1 магнитное поле тока I1, B2 магнитное поле тока I2.
dV dV dV полевая трактовка энергии, где B1 магнитное поле тока I1, B2 магнитное поле тока I2.
ЗАДАЧИ ЭДС индукции, ЭДС самоиндукции:
1. Провод, имеющий форму параболы y = kx2 , находится в однородном магнитном поле B! , перпендикулярном плоскости параболы. Из вершины параболы перемещают поступательно и без начальной скорости перемычку с постоянным ускорением a. Найти ЭДС индукции в образовавшемся контуре как функцию времени.
Решение:
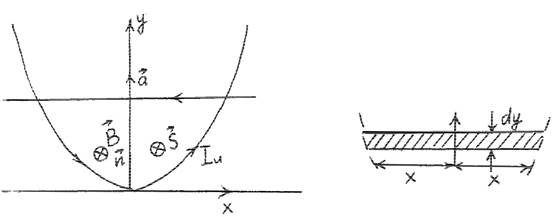
За время dt перемычка переместится на dy , и замкнутый контур получит приращение площади dS = 2xdy .
Если S! ↑↑ B! , то dΦ = BdS .
Поток Φ возрастает и индукционный ток Iи течет против часовой стрелки, порождая поле B!и ↑↓ B! компенсируя изменение Φ .
 Тогда εи = − ddtΦ = −B 2xdydt . Но dydt = v = at , x = ky = at2k2 .
Тогда εи = − ddtΦ = −B 2xdydt . Но dydt = v = at , x = ky = at2k2 .
![]()
![]() Поэтому εи =
−B⋅2at at2k2 =
−Ba 2kat2.
Поэтому εи =
−B⋅2at at2k2 =
−Ba 2kat2.
Ответ:  Ba
Ba ![]() t2.
t2.
2. Плоская спираль с большим числом N витков, плотно прилегающих друг к другу, находится в однородном магнитном поле, перпендикулярном в плоскости спирали. Наружный радиус спирали равен a. Магнитное поле изменяется со временем по закону B = B0 sinωt . Найти амплитудное значение ЭДС индукции, наведенной в спирали.
Решение:
Выделим участок спирали толщиной dr . В нем dN = Na dr витков по форме совпадающих с окружностью радиуса r .
Полный магнитный поток через этот участок спирали равен dΦ = B r dNπ 2 = B Nπa r dr2 .
Полный магнитный поток через всю спираль равен
Φ = ∫0a dΦ = B Nπa r33 ![]() 0a=πNa3 2 B0 sinωt.
0a=πNa3 2 B0 sinωt.
Тогда ![]()
![]() B t и амплитуда εи0 =
−πNa3 2ωB0.
B t и амплитуда εи0 =
−πNa3 2ωB0.
Ответ: εи0 = −πNa3 2ωB0.
3.
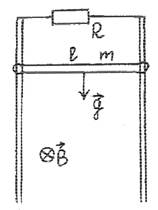 По двум металлическим
столбам, поставленным вертикально
По двум металлическим
столбам, поставленным вертикально
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.