Электрическое поле в вакууме. Основные определения и формулы. Электрический заряд. Принцип суперпозиции

Линии вектора _E^! выходят из источников поля и заканчиваются в местах стоков.

Теорема      о        циркуляции:         циркуляция          вектора       _E^! в        любом электростатическом поле равна нулю: "∫ Edl^! = 0.

Потенциал  это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля: ϕ( )r  потенциал.

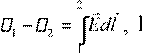 и 2  точки между которыми перемещается заряд.

Потенциал поля точечного заряда:ϕ⁼ _4πεε¹ 0 ^q_r .

Потенциал поля системы зарядов: ϕ= _4λεε¹ 0 _∑ ^q_riⁱ , где r_i  расстояние от точечного заряда q_i до интересующей нас точки поля.

Если заряды распределены непрерывно: ϕ= _4πεε¹ 0 _∫^ρdV_r     .

Связь напряженности и потенциала: E^! = −∇^!ϕ.

Эквипотенциальная поверхность  поверхность во всех точках которой потенциал ϕ имеет одно и то же значение.

Электрический диполь:

Электрический диполь  это система из двух одинаковых по модулю разноименных точечных зарядов +q и −q, находящихся на некотором расстоянии l друг от друга.

ϕ= 4πεε1 0  rq+ − rq−  = 4πεε1 0 q r( )( )(r+⁻ −rr−⁺) . ϕ= 1 pcos₂ ϑ, где p^! = ql^!  электрический момент диполя.

        4λεε₀       r

Сила, действующая на диполь: F^! = p^{! ∂}_∂^E_l! .

Момент сил, действующих на диполь: M^! = _p E^!, ^!_ .

Этот момент сил стремится повернуть диполь так, чтобы его электрический момент _p^! установился по направлению внешнего поля _E^! . Энергия поля в диполе: W = −pE^!! .

ЗАДАЧИ

Дискретный заряд

1. Четыре свободных электрических заряда +q, +q, −Q,  и  −Q неподвижно  лежат на горизонтальной поверхности, удерживаемые в положении неустойчивого равновесия силами Кулона. Определить наибольший угол четырехугольника, образованного этими зарядами.

Решение:

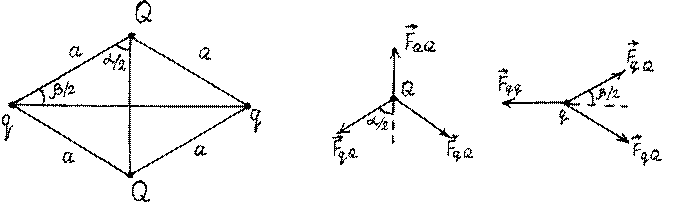
Запишем условие равновесия сил, действующих на заряды q и Q:

FQQ = 2FqQ cosα2 

Fqq = 2FqQ cos β2  или

4πε1 0 2acosQ2 α = 2 qQ 2 cosα2 

2

                                     4πε0a

1               q          = 2          2             2

4πε0 2acos2 β22 2 4πεqQa cos β

                                           0

 или

Q = 8qcos3 α2  , q = 8Qcos³ β2 _

Получаем 64cosα β2 cos 2 3 =1, но так как cos β2 = cosπ α2 − 2  = sinα2 , то 

8 2^ cos^{α α}2 sin 2 ^_³ =1 или sin³α= ¹₈ , sinα= ¹₂ , т.е. α= 30^# , β=180^# −α=150^# .

Ответ: больший угол равен 150°

2. Два точечных положительных заряда q ₁ = 1,2^. 10 ⁷ Кл, q ₂ = 3^. 10 ⁸ Кл закреплены на противоположных концах деревянного стержня длины b = 8,1 м. Найти минимум потенциала, созданного этими зарядами в точках стержня.

Решение:

 

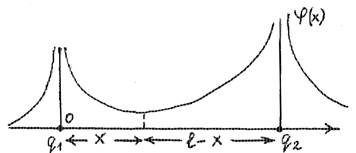
Согласно принципу суперпозиции ϕ= _4πε¹ 0 ^_ ^q_x¹ + _l^q₋²_x ^_,

Условие минимума ∂∂ϕx = − xq12 + (l −q2x)2  = 0, т.е. q1 (l − x) =                                                    q x2                                   , т.о.

x = 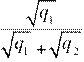l .

Чтобы убедиться, что это действительно минимум находим вторую производную ^∂_x²    , если ^∂_x²          0  минимум, если ^∂_x²         0  максимум.

Тогда ϕmin = 4πε1 0 ^ q1 ( ql1 + q2 )+ q2 ( ql1 +  q2 ⁾^ ₌ ( q14πε+ 0q2 )² _{= 300В}.

                                                                                        

Ответ: ϕ_min = 300В

3.  Точечные заряды q ₁ = 2,7^. 10 ⁸ Кл  и q ₂ = 6,4^. 10 ⁸ Кл закреплены на противоположных концах диаметра окружности с радиусом R = 15 м.

Найти минимальное значение величины напряженности электростатического поля, созданного этими зарядами в точках окружности.

Решение:

В подобных задачах брать производную легче по угловой переменной α, чем по переменным x = 2Rcosα, y = 2Rsinα.

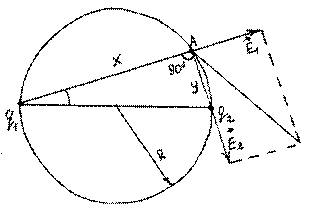
В точке А имеем

E

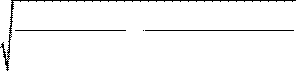
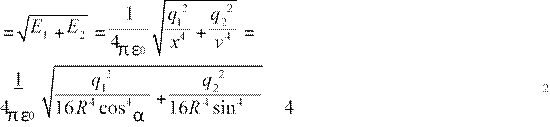                                                                                1               q12             2 +      2         q 2     2           ²

=                                              =

                                                                         ^{α πε}₀ (4R2 cos2α)      (4R (1−cos α))

Условие экстремума: ,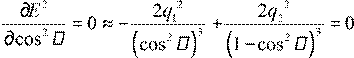 

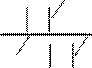
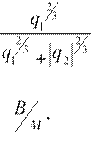
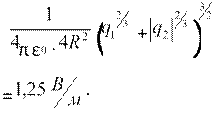т.е. 1−cos2α=  qq21 23 cos2α, ⇒ cos2α=, sin2α= q123q+2 2q32 23 .



Тогда E_min ==1,25

Ответ: E_min

Равномерно распределенный заряд

4.  В какой точке на оси тонкого кольца, заряженного равномерно, на точечный заряд q₀ будет действовать максимальная сила? Радиус кольца равен R.

Решение:

Любой непрерывно распределенный заряд надо разбивать на «точечные» заряды dq, для которых можно использовать закон Кулона: dF^! = _4πε¹ 0 ^{q dq}_r⁰ ₂ , осталось только взять интеграл по всем dq.

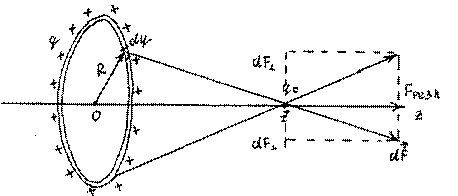
Используем симметрию задачи: _F^!_рез направлена по оси 0z, поэтому надо суммировать только проекции _dF^! на ось z:

F_рез dF   dq.

r² = z² + R² и cosθ =     z₂ ^z_{+ R}2 , 

Т.о. F_рез ⁼ ₄^{q q}_πε⁰ 0 _(R2 ₊^z_z2 ₎32  сила, действующая на точечный заряд q₀ на оси равномерно заряженного кольца на расстоянии z от его центра 0. Этот же результат можно получить проще, через потенциальную энергию взаимодействия зарядов:

W = ∫ 4πε1 0 dq qr⋅ 0 = 4πε0 qqR02 + z2 .

F_рез = −gradW  направлена по оси 0z, т.е.: 

Fрез = − dzd W = − 4qqπε00 dzd  R21+ z2  = 4qqπε00 (R2 +zz2 )32 .

Теперь находим максимум F_рез :

                        (R2 + z2 )32 − z⋅ 3 (R2 + z2 )12 ⋅2z          или R² + z² −3z² = 0, 2z2 = R2 ,

z = ^R  в этой точке F_рез будет максимальной и равной  2

Fрезmax = 4q qπε0 0  32RR2 2_32 = 6 3q qπε0   0R2 .

Ответ: Fрезmax = 6 3q qπε0     ₀R2 .

5. Тонкое кольцо радиуса R заряжено равномерно и имеет положительный заряд q. Вдоль оси кольца расположен тонкий стержень длины 3R, равномерно заряженный с той же плотностью, что и кольцо. Плоскость кольца делит стержень в пропорции 1:2, найти силу, действующую на стержень.

Решение:

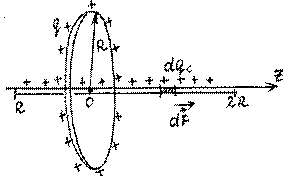
Разбиваем стержень на малые точечные заряды dq_c = λdz , где λ  линейная плотность заряда λ= q2πR. Из задачи 4 возьмем выражение для силы, действующей на этот заряд: .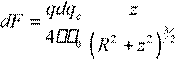

Полная сила, действующая на стержень:

F = ∫dF = −∫R 4πεqλ0 (z2 +zdzR2 )32 = 16πεq22 0R 4R∫R22 (z2 +dzR22 )32 , 2R

совершаем замену переменной: x = z² + R² ,

получаем F = _16πεq22 _R 5R22 x−32dx =        q22 R (−2x−12 ) 52RR22 = 8πεq2 20R     21R2 − 51R2 или ∫

                                               0      2R                          16πε0

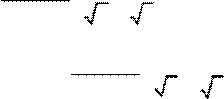F = 8πε2q²₀R2 _ 12 ₋ 15 _ . Ответ: F =   2q2 R2  12 − 15  .

8πε0

6. Диск радиуса R заряжен равномерно с поверхностной плотностью заряда σ. Найти потенциал  и напряженность поля на оси диска.

Решение:

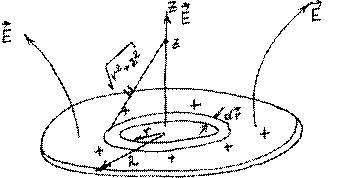
Разбиваем диск на тонкие кольца радиуса r и толщины dr с зарядом