Построение функции одномерной полезности. Построение функции полезности, получение ее аналитического и графического вида

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

теория выбора и принятия решений

Лабораторная работа № 2

построение функции одномерной полезности

Выполнил: ст. гр.                                                              

Проверил:                                                                                        

Тула 2005

ЦЕЛЬ

Закрепление теоретических знаний по теории одномерной полезности, изучение методики практического построения функции одномерной полезности.

ЗАДАНИЕ

1.  Изучить основные положения теории одномерной полезности и методику построения функции одномерной полезности.

2.  Согласно методике провести опрос лица, принимающего решение в заданной области.

3.  Провести построение функции полезности, получить ее аналитический и графический вид.

4.  Проанализировать полученные результаты.

ВЫПОЛНЕНИЕ

1.  Описание ситуации

Пусть в жилом квартале города организуется новый универсальный магазин самообслуживания. Необходимо определить количество касс на выходе их торгового зала, в которых покупатели будут рассчитываться за покупки с целью снизить время, которое им придется отстоять в очереди. Торговый зал способен вместить до 200 покупателей одновременно, на расчет с одним покупателем обычно тратится 30 секунд.

2. Протокол диалогового опроса лица, принимающего решение и построение функции полезности

В качестве альтернатив (возможных вариантов действий) выступают решения, связанные с возможным количеством касс , устанавливаемых в торговом зале.

Для каждой альтернативы можно определить множество исходов, характеризующих число пришедших покупателей .

Для того чтобы характеризовать каждую альтернативу одним числом, введем оценочную функцию вида . Пусть таким критерием принятия решения служит число секунд, простаиваемое покупателем в очереди торгового зала, вычисляемое по формуле .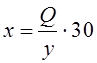

Ограничим область исследуемых предпочтений. Будем рассматривать .

При опросе лица, принимающего решения, получены следующие сведения.

Если , всегда ли  предпочтительнее  ? Нет.

Если , всегда ли  предпочтительнее  ? Да.

Отсюда можно сделать вывод, что исследуемая функция полезности монотонно убывает.

Исследуем склонность лица, принимающего решения к риску.

Предпочтительнее ли лотерея , чем ожидаемый выигрыш  при любых  и ? Нет.

Отсюда можно сделать вывод о несклонности лица, принимающего решения к риску.

Определим тип монотонности отношения к риску.

Известно, что принимающий решение обладает убывающей несклонностью к риску, если 1) он несклонен к риску; 2) надбавка за риск  в любой лотерее для него уменьшается при увеличении опорной суммы .

Для монотонно убывающих функций полезности надбавка за риск вычисляется по формуле

, где  — детерминированный эквивалент,  — ожидаемый выигрыш.

Пусть для лица, принимающего решения, одинаково предпочтительны возможности:

1) 50% вероятности того, что покупатели простоят в очереди 100 и 140 секунд и гарантированная возможность прохождения очереди за 135 секунд, ;

2)  50% вероятности того, что покупатели простоят в очереди 140 и 250 секунд и гарантированная возможность прохождения очереди за 195 секунд, ;

3) 50% вероятности того, что покупатели простоят в очереди 100 и 200 секунд и гарантированная возможность прохождения очереди за 155 секунд, .

Делаем вывод о том, что принимающий решение обладает убывающей несклонностью к риску.

Вид функции полезности ищем в виде , .

Пусть лицо, принимающее решение, присвоило следующие значения полезности:

, , .

Тогда, решив систему трех нелинейных уравнений, найдем неизвестные коэффициенты:

> solve({a+5*b+5^2*c=400,a+300*b+300^2*c=5,a+150*b+150^2*c=300},{a,b,c});

> evalf(%);

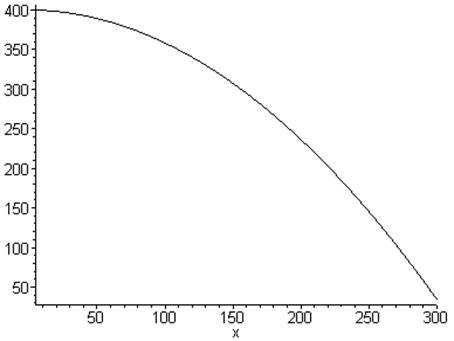
> plot(400.201-0.019*x-0.004*x^2,x=5..300,color=black);