Построение функции одномерной полезности. Закрепление теоретических знаний по теории одномерной полезности, изучение методики практического построения функции одномерной полезности

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

ТЕОРИЯ  ВЫБОРА  И  ПРИНЯТИЯ  РЕШЕНИЙ

Лабораторная  работа  №2

«Построение  функции  одномерной  полезности»

Выполнил студент группы                            

Принял                                                                         

Тула - 2005

Цель работы

Закрепление теоретических знаний по теории одномерной полезности, изучение методики практического построения функции одномерной полезности.

Постановка задачи

Пусть в жилом районе города организуется новый универсальный магазин самообслуживания ( по аналогии с супермаркетами). Необходимо определить количество кассовых пунктов на выходе из торгового зала, в которых покупатели будут рассчитываться за покупки с целью снизить время, которое им придётся отстоять в очереди. Торговый зал в силах вместить до 200 покупателей одновременно, на расчёт с одним покупателем обычно тратится 30 секунд.

Выполнение

Имеем задачу выбора в условиях риска. Критерием принятия решения служит время, которое покупатель простоит в очереди.

Пусть минимальное значение кассовых пунктов равно 5, тогда время обслуживания 200 покупателей составит 20 минут. Максимальное значение составляет 15 пунктов, время – 6,6 минут. Имеем границы изменения времени [6,6;20].

Так как нам необходимо уменьшить время обслуживания, то меньшее значение времени будет предпочтительнее большего. Это свидетельствует о монотонном убывании функции полезности. Из того, что лицо принимающее решение предпочитает ожидаемый выигрыш, следует его несклонность к риску.

Диалоговый опрос исследуемого лица дал следующие результаты:

1) для него одинаково предпочтительны возможности 50%-ой вероятности ожидания покупателя 7 минут и 12 минут и гарантированного ожидания 10 минут;

2) для него одинаково предпочтительны возможности 50%-ой вероятности ожидания покупателя 10 минут и 15 минут и гарантированного ожидания 13 минут;

3) для него одинаково предпочтительны возможности 50%-ой вероятности ожидания покупателя 13 минут и 20 минут и гарантированного ожидания 16 минут.

Детерминированные эквиваленты следующие:

[7;12]        x_d=8,5;

[10;15]      x_d=11;

[13;20]      x_d=14,5.

Определим надбавку за риск:

8,5-9,5=-1;

11-12,5=-1,5;

14,5-16,5=-2.

Полученные данные показывают, что склонность к риску имеет убывающую тенденцию.

Будем искать функцию полезности в экспоненциальной форме

.

Присвоим значениям критерия x=6,8,10,14,18 значения полезности U(x)=10,8,6,4,3 соответственно.

Тогда неизвестные параметры функции найдём из системы нелинейных уравнений

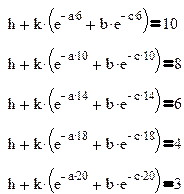Получаем функцию полезности в виде

.

Графический вид функции полезности следующий.

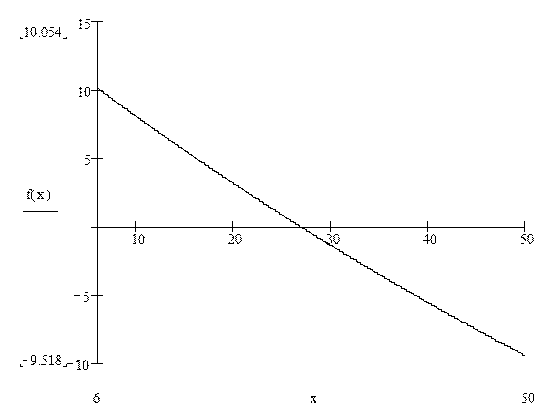Таким образом видим, что максимальное значение полезности достигается при x=6 минут (20 кассовых пунктов). Решением задачи в данном случае будет 15<x<20.