Основные критерии принятия решений. Минимаксный критерий (ММ). Критерий Гермейера (G). Таблица потерь прибыли

Цель работы

Изучить основные критерии принятия решений.

Постановка задачи

1. Необходимо применить критерии принятия решения к задаче.

Пусть некоторую машину требуется проверить с приостановкой её эксплуатации. Из-за этого приостанавливается выпуск продукции. Если же неисправность не обнаружить, то это приведёт не только к приостановке, но и к поломке машины, а значит – к ещё большим потерям.

Варианты решения таковы:

Е₁ – полная проверка;

Е₂ – минимальная проверка;

Е₃ – отказ от проверки.

Машина может находиться в следующих состояниях:

F₁ – неисправностей нет;

F₂ – имеется незначительная неисправность;

F₃ – имеется серьёзная неисправность.

	F1	F2	F3
Е1	-20	-22	-25
Е2	-14	-23	-31
Е3	0	-24	-40

Результаты e_ij являются затратами, связанными с проверкой и потерями продукции.

Произвести сравнение результатов полученных по различным критериям и дать заключение о применимости критериев к данной задаче.

2. Разработать задачу принятия решения (матрица решения n x m, причём n, m  5). Выбрать и обосновать использование критерия для её решения.

Выполнение

Опишем критерии, которые будем использовать при решении задач, минимаксный и Гермейера.

Минимаксный критерий (ММ).

Этот критерий соответствует позиции крайней осторожности.

Оценочная функция

,

.

Таким образом, при выборе оптимального решения  справедливо соотношение

.

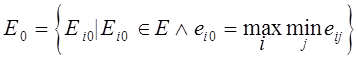Критерий Гермейера (G).

Этот критерий ориентирован на величины потерь, т. е. на отрицательные значения всех .

Оценочная функция

,

.

Оптимальное решение

.

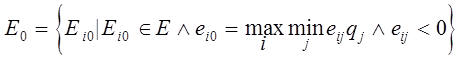В случае, когда встречаются >0, то переходят к строго отрицательным значениям с помощью преоьразования -а (однако, следует иметь в виду, что оптимальный вариант решения будет зависеть от а).

G-критерий обобщает ММ-критерий. В случае равномерного распределения  они становятся идентичными.

Условия применимости критерия:

-вероятности появления состояния  известны;

-с появлением тех или иных состояний отдельно или в комплексе необходимо считаться;

-допускается некоторый риск;

-решение может реализоваться один или много раз.

1. Применим к задаче ММ-критерий.

Получаем Z_мм=-25. Таким образом, по данному критерию следует выбрать Решение Е₁ (полная проверка).

Добавим следующее распределение вероятностей состояний q_j:

F₁-0.3; F₂-0.6; F₃-0.1.

Применим G-критерий. Получим Z_G=-13.2 и решение Е₁.

Таким образом, результаты решения задачи по двум критериям совпадают и имеем решение, которое предполагает полную проверку оборудования.

2. Применим заданные критерии к разработанной задаче.

Пусть имеется некоторая партия товара с ограниченным сроком хранения,.которую необходимо реализовать. С течением времени срок хранения уменьшается, спрос на товар падает и партия реализуется не полностью. Продавец принимает решение снижать цену на товар с течением времени для поддержания спроса, что также приводит к потерям в прибыли.

Варианты решения таковы:

Е₁ – цена 100%;

Е₂ – снижена на 5%;

Е₃ – снижена на 7%;

Е₄ – снижена на 10%;

Е₅ – снижена на 15%.

Товар может находиться в следующих состояниях:

F₁ – срок хранения полный;

F₂ – осталось 10 дней;

F₃ – осталось 8 дней;

F₄ – осталось 5 дней;

F₅ – осталось 2 дня.

Таблица потерь прибыли.

	F1	F2	F3	F4	F5
Е1	0	-2	-3	-7	-15
Е2	-3	-1	-2	-9	-16
Е3	-6	-4	-5	-8	-19
Е4	-11	-8	-6	-3	-10
Е5	-20	-15	-10	-6	-1

Вероятности реализации товара при различном сроке хранения таковы:

(0.34; 0.29; 0.18; 0.11; 0.08).

Имеем решение.

ММ-критерий: Z_MM=-10; решение Е₃.

G-критерий: Z_G=-1.2; решение Е₁.

Результаты не совпадают. Но, так как G-критерий учитывает вероятности наступления состояний, то за результат примем решение Е₁- цена не снижается.