



анализируемой случайной величины (t), произведенных в последовательные моменты времени t1,t2,...,tN, называется временным рядом. Определение временного ряда опирается на понятие случайной величины (t), зависящей от параметра t, интерпретируемого как время. Это значит, что закон распределения вероятностей этих случайных величин, и в частности, их первые и вторые моменты, также, вообще говоря, могут зависеть от времени t.
Взаимозависимость
членов временного ряда создает свою специфическую базу для построения
прогнозных значений анализируемого показателя (т.е. для построения оценок ![]() для неизвестных
значений
для неизвестных
значений ![]() ) по
наблюденным значениям x(1),x(2),...,x(N). Или временной ряд удобнее представлять в
виде:
) по
наблюденным значениям x(1),x(2),...,x(N). Или временной ряд удобнее представлять в
виде:
![]() (1)
(1)
где x(t) — значение анализируемого показателя, зарегистрированное в t-м такте времени (t = 1,2,..., N).
Стационарные временные ряды и их основные характеристики.
Поиск модели, адекватно описывающей поведение случайных остатков ε(t) анализируемого временного ряда x(t), производят, как правило, в рамках некоторого специального класса случайных временных последовательностей – класса стационарных временных рядов. На интуитивном уровне стационарность временного ряда мы связываем с требованием, чтобы он имел постоянное среднее значение и колебался вокруг этого среднего с постоянной дисперсией. В некоторых случаях временные последовательности этого класса могут воспроизводить и поведение самого анализируемого временного ряда x(t).
Ряд x(t) называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей m наблюдений x(t1),x(t2),...,x(tm) такое же, как и для m наблюдений x(t1+τ),x(t2+τ),...,x(tm+τ), при любых m, t1,t2,...,tm и τ.
Свойства строго стационарного временного ряда не меняются при изменении начала отсчета времени. В частности, при m = 1, из предположения о строгой стационарности временного ряда x(t) следует, что закон распределения вероятностей случайной величины x(t) не зависит от t, а значит, не зависят от t и все его основные числовые характеристики, в том числе: среднее значение Ex(t) = a и дисперсия Dx(t) = E(x(t) - а)2 = σ2.
Значение а определяет постоянный уровень, относительно которого флуктуирует анализируемый временной ряд x(t), а постоянная величина а характеризует размах этой флуктуации. Поскольку закон распределения вероятностей случайной величины x(t) одинаков при всех t, то он сам и его основные числовые характеристики могут быть оценены по наблюдениям x(1),x(2),...,x(N). В частности:
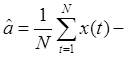 оценка среднего значения,
оценка среднего значения,
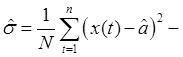 оценка дисперсии.
оценка дисперсии.
Автоковариационная функцияγ(r). Из предположения о строгой стационарности временного ряда x(t) при m = 2 следует, что совместные двумерные распределения для пар случайных величин (x(t1), x(t2)), (x(0), x(t2 – t1)), (x(τ), x(t – t + τ)) совпадают при любых t1, t2 и τ и зависят только от разности t2 – t1. Соответственно, ковариация между значениями x(t) и x(t ± τ) будет зависеть только от величины «сдвига по времени» τ (и не будет зависеть от t). Эта ковариация называется автоковариацией (поскольку измеряет ковариацию для различных значений одного и того же временного ряда x(t)) и определяется соотношением:
![]() .
.
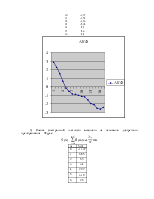
Значения автоковариационной функции могут быть статистически оценены по имеющимся наблюдениям временного ряда (1) по формуле
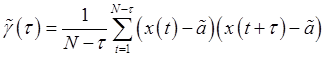 , где r = 1, 2, ... , N – 1.
, где r = 1, 2, ... , N – 1.
Спектральная плотность p(ω). Определим спектральную плотность стационарного временного ряда x(t) через его автокорреляционную функцию r(τ) соотношением вида:
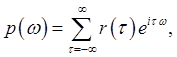
где i = ![]() (мнимая единица). Благодаря
тому, что r(τ) = r(–τ),
спектральная плотность р(ω) может быть записана в виде:
(мнимая единица). Благодаря
тому, что r(τ) = r(–τ),
спектральная плотность р(ω) может быть записана в виде:
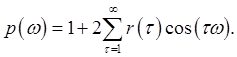
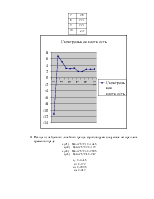
Функция является гармонической и имеет период 2π. Поскольку cos [(2π — ω)τ] = cos(ωτ), то график спектральной плотности р(ω), называемый спектром, симметричен относительно ω= π. Поэтому при анализе поведения функции р(ω) ограничиваются значениями ω, лежащими между 0 и π. Расчет по формуле:
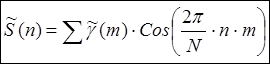
Прогноз. Проблема прогнозирования – это кратко-
и среднесрочный прогноз, поскольку построение долгосрочного прогноза
подразумевает обязательное использование методов организации и статистического
анализа специальных экспертных оценок. Тем не менее, использование
доступных к моменту времени t = N наблюдений временного ряда (1) для прогнозирования значения x(t) на один или
несколько временных тактов вперед (т. е. – для прогнозной оценки значений ![]() , l = 1,2,3) может явиться основой для:
, l = 1,2,3) может явиться основой для:
ü планирования в экономике, производстве, торговле;
ü управления и оптимизации протекающих в обществе социально-экономических процессов;
ü частичного управления важными параметрами демографических процессов и экологической ниши общества;
ü принятия оптимальных решений в бизнесе.
На
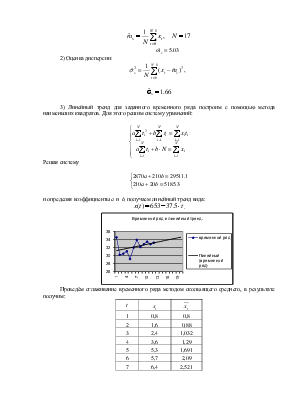
основе визуального анализа графика делается вывод о форме аналитической кривой,
способной наилучшим образом аппроксимировать ломанную на графике. В данном
случае такой кривой является парабола ![]() .
Для определения исходно неизвестных параметров параболы
.
Для определения исходно неизвестных параметров параболы ![]() , согласно
, согласно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.