Приобретение навыков расчета характеристик временных рядов и построение прогноза.
Дан временной ряд естественного движения всего (сельского и городского) населения
|
Годы t |
Число разводов на 1000 населения Xt |
|
1980 |
4.8 |
|
1985 |
4.8 |
|
1990 |
4.3 |
|
1995 |
5.0 |
|
1996 |
3.9 |
|
1997 |
3.6 |
|
1998 |
3.6 |
|
1999 |
3.8 |
|
2000 |
4,5 |
|
2001 |
5.3 |
Необходимо :
1) найти оценку математического ожидания;
2) найти оценку дисперсии;
3) построить линейный тренд;
4) найти оценку корреляционного момента;
5) найти оценку спектральной плотности;
6) спрогнозировать следующие члены данного временного ряда.
1) Оценка математического ожидания:
![]()
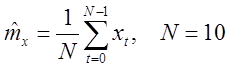
![]()
2) Оценка дисперсии:
![]()
![]()
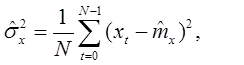
![]()
3) Линейный тренд для заданного временного ряда построим с помощью метода наименьших квадратов. Для этого решим систему уравнений:
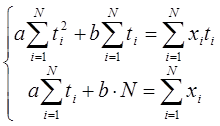
Решая эту систему и определяя коэффициенты a и b, получаем линейный тренд вида:
![]()
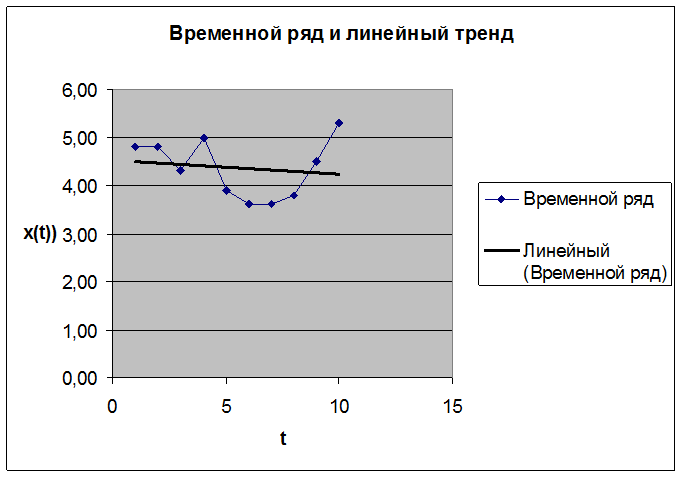
Проведём сглаживание временного ряда методом скользящего среднего, в результате получим:
|
t |
|
|
|
1 |
4.8 |
4,8 |
|
2 |
4.8 |
4,8 |
|
3 |
4.3 |
4,63 |
|
4 |
5.0 |
4,7 |
|
5 |
3.9 |
4,4 |
|
6 |
3.6 |
4,17 |
|
7 |
3.6 |
3,7 |
|
8 |
3.8 |
3,67 |
|
9 |
4,5 |
3,97 |
|
10 |
5.3 |
4,53 |
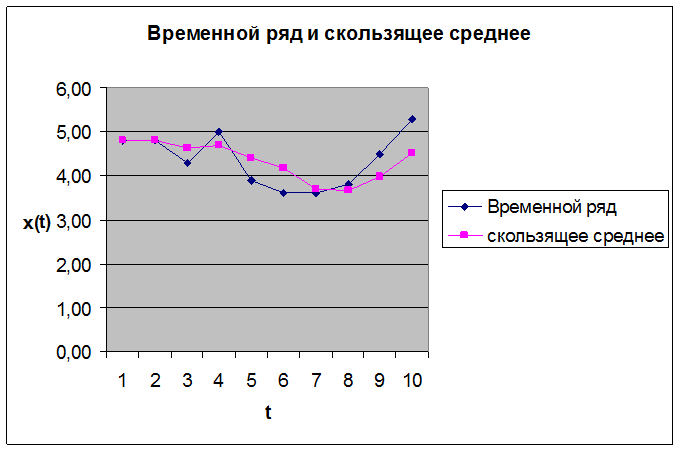
4) Оценка автокорреляционной функции:
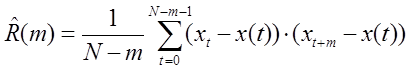 .
.
|
m |
|
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
.24 |
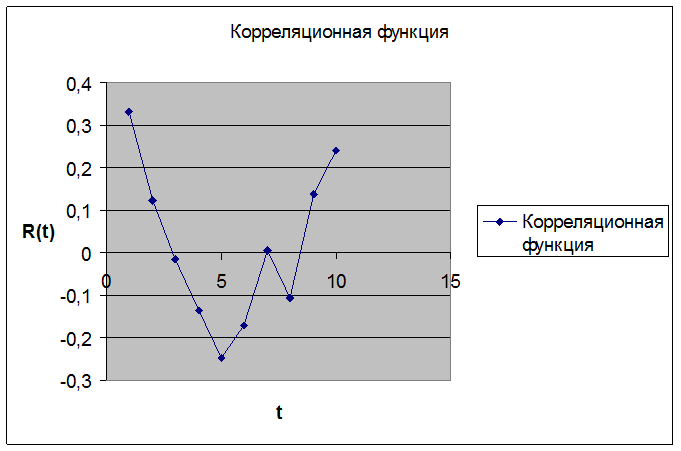
5) Оценка спектральной плотности мощности на основании дискретного преобразования Фурье:
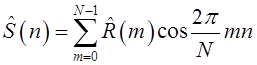 .
.
|
m |
|
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
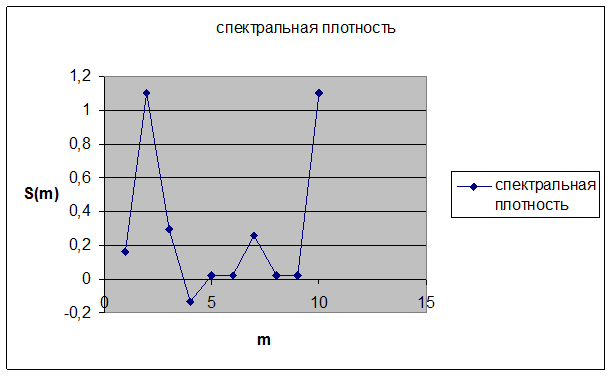
7) Исходя из найденного линейного тренда, спрогнозируем следующие четыре члена временного ряда:
x10 =4,2
x11=-4,17
x12 =-4,14
x13 =-4,11.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.