Временной ряд на основе статистических данных по среднегодовым ценам на акции некоторой фирмы

Министерство образования и науки Российской Федерации

Тульский государственный университет

Кафедра ПМиИ

Прикладной анализ временных рядов

Расчётная работа

Выполнил: ст. гр.                                                                  

Проверил:                                                                                           В

.

Тула-2004.

Рассмотрим временной ряд на основе статистических данных по среднегодовым ценам на акции некоторой фирмы.

годы	1990	1991	1992	1993	1994	1995	1996
цена	47.6	49.6	53.6	55.6	58.6	59.6	63.6
годы	1997	1998	1999	2000	2001	2002	2003
цена	64.6	56.6	60.6	76.3	86.6	96.3	66.6

1.  Основные характеристики ряда:

Математическое ожидание: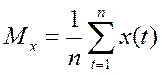                

Дисперсия: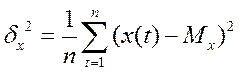                             

Среднеквадратическое отклонение:                             

Коэффициенты автоковариации:

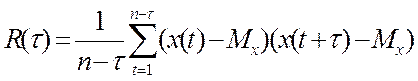
Коэффициенты автокорреляции найдем по формуле:

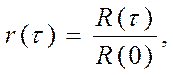
0	177.231	1
1	124.227	0.701
2	56.101	0.316
3	5.217	0.029
4	-3.355	-0.019
5	9.89	0.056
6	-9.222	-0.052
7	-33.777	-0.19
8	-55.551	-0.313
9	-128.319	-0.724
10	-221.158	-1.247
11	-287.522	-1.621
12	-283.551	-1.599
13	-42.837	-0.242

Графическое представление временного ряда:

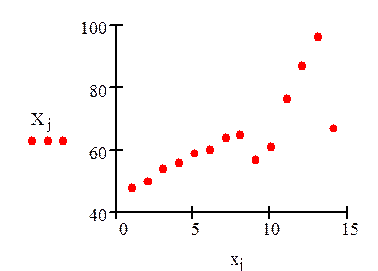
Коррелограмма временного ряда:

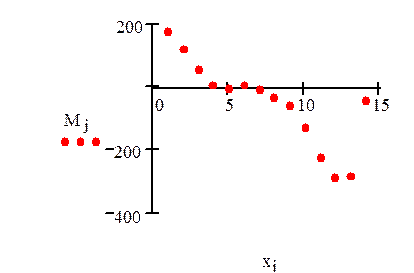
2.  Проведём сглаживание временного ряда методом скользящего среднего.

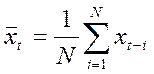,  - число предшествующих периодов

В результате получим:

t	1	2	3	4	5	6	7
	47.6	49.6	53.6	55.6	58.6	59.6	63.6
	47.6	48.6	50.3	51.6	53	54.1	55.5
t	8	9	10	11	12	13	14
	64.6	56.6	60.6	76.3	86.6	96.3	66.6
	56.6	56.6	57	58.8	61.1	63.8	64

Графическое представление сглаженного временного ряда

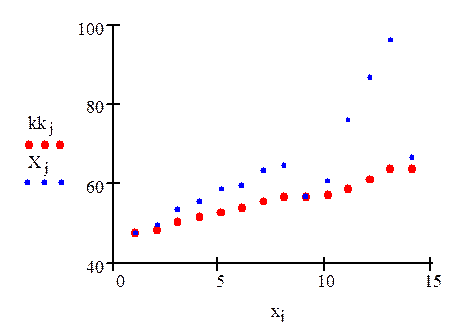
Проведём экспоненциальное сглаживание временного ряда:

где возьмем α=0,5

t	1	2	3	4	5	6	7
	47.6	48.6	53.6	55.6	58.6	59.6	63.6
	47.6	48.6	51.6	54.6	57.1	59.1	61.6
t	8	9	10	11	12	13	14
	64.6	56.6	60.6	76.3	86.6	96.3	66.6
	64.1	60.6	58.6	68.5	81.5	91.5	81.5

Экспоненциальное сглаживание:

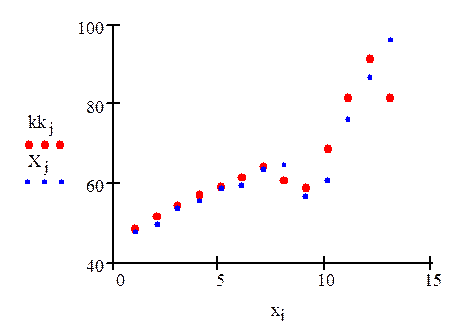
3. Линейный тренд построим с помощью метода наименьших квадратов

                

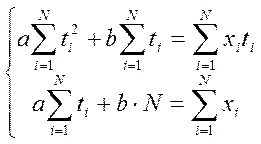
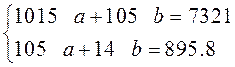
Решив эту систему, получаем линейный тренд вида:

Графическое представление:

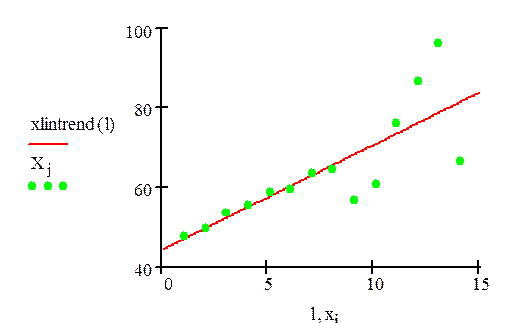
1	2	3	4	5	6	7
46.8	49.4	52.1	54.7	57.4	60.0	62.7
8	9	10	11	12	13	14
65.3	68.0	70.6	73.3	75.9	78.6	81.2

4. Вычтем тренд из временного ряда. Получаем следующие остатки:

1	2	3	4	5	6	7
0.8	0.2	1.5	0.9	1.2	-0.4	0.9
8	9	10	11	12	13	14
-0.7	-11.4	-10.0	3.0	10.7	17.7	-14.4

Графическое представление остатков исходного ряда:

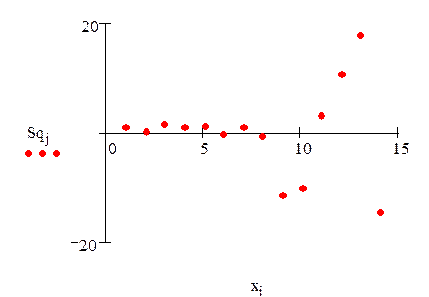
Основные характеристики для остатков:

Математическое ожидание:                        

Дисперсия:                                                   

Среднеквадратическое отклонение:             

5.Произведем сглаживание остатков временного ряда:

Методом скользящего среднего:

1	2	3	4	5	6	7
0.83	0.5	0.85	0.86	0.93	0.71	0.74
8	9	10	11	12	13	14
0.56	-0.76	-1.69	-1.26	-0.26	1.13	0.002714

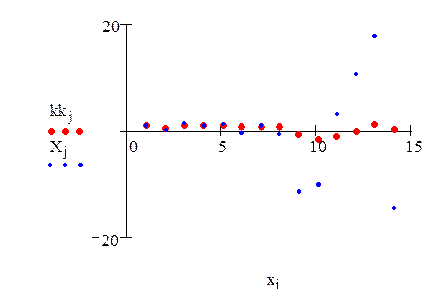
Экспоненциальное сглаживание:

1	2	3	4	5	6	7
	0.5	0.86	1.21	1.06	0.41	0.27
8	9	10	11	12	13	14
0.12	-6.03	-10.68	-3.48	6.88	14.23	1.58

6. Оценка спектральной плотности мощности на основании дискретного преобразования     Фурье:

.

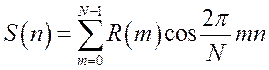1	2	3	4	5	6	7
-692.54	261.95	687.5	377.88	135.48	92.16	26
8	9	10	11	12	13	14
13.71	26	92.16	135.48	377.88	687.5	261.95

Графическое представление спектральной плотности:

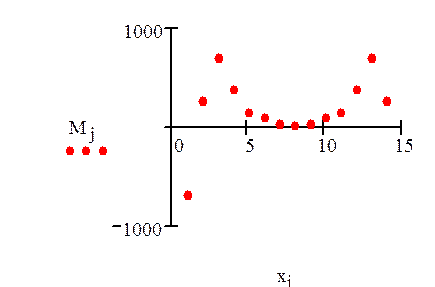
7.Исходя из найденного линейного тренда, спрогнозируем следующие три члена временного ряда:

x₁₅ =83.8;

x₁₆ =86.5;

x₁₇ =89.1.