Прикладной анализ временных рядов. Посевная площадь Тульской области. Изучение методов анализа временных рядов

Министерство образования РФ

Тульский Государственный Университет

Кафедра Прикладной Математики и Информатики

ПРИКЛАДНОЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

Контрольно-курсовая работа

Выполнил: студент гр.                                                         

Принял:                                                                                                       

Тула – 2003

ЦЕЛЬ РАБОТЫ

Изучение методов анализа временных рядов.

ИСХОДНЫЕ ДАННЫЕ

Дан временной ряд

                                 Таблица 1. Посевная площадь Тульской  области

ЗАДАНИЕ

  найти оценку математического ожидания;

  найти оценку дисперсии;

  построить тренд;

  найти оценку корреляционного момента;

  найти оценку спектральной плотности;

  спрогнозировать следующие члены данного временного ряда.

ВЫПОЛНЕНИЕ

1) Оценка математического ожидания ищется по формуле:

.

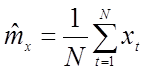1239,87.

2) Оценка дисперсии:

.

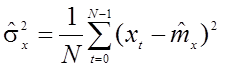   223,85.

3)  Для расчета тренда рассмотрим заданный ряд.

Рис. 1 Временной ряд изменения количества  посевных площадей Тульской области

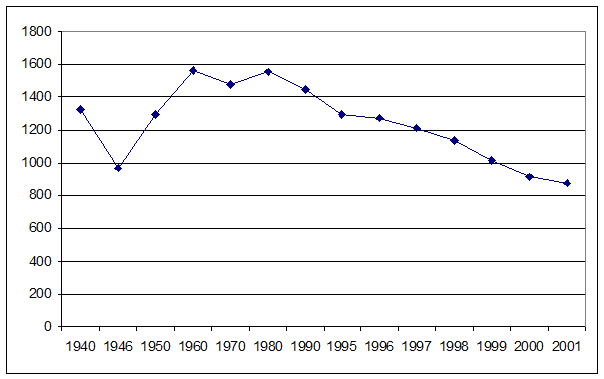
Исходя из внешнего вида временной зависимости, будем рассчитывать  тренд в виде полинома .

Воспользуемся методом наименьших квадратов:

.

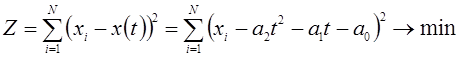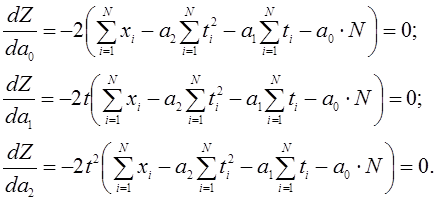
Получим систему линейных уравнений

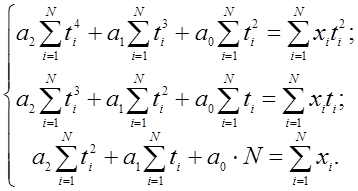
Решая систему

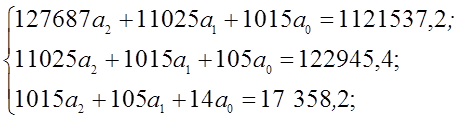
получим значения коэффициентов :

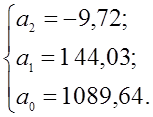
Получим полиномиальный тренд вида

.

Рис.2 Временной ряд и полиномиальный тренд

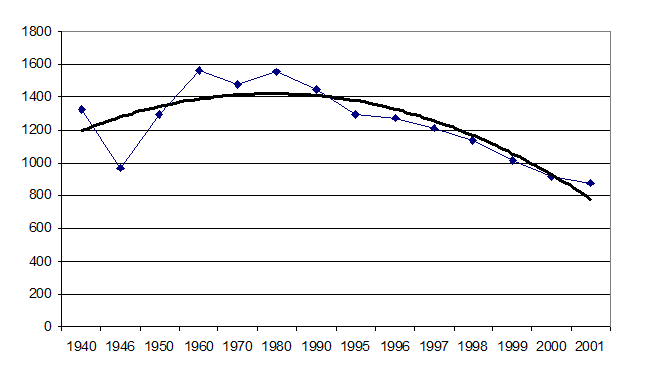
Проведем сглаживание ряда методом скользящего среднего:

Таблица 2. Сглаживание ряда методом скользящего среднего

Рис. 3 Исходный ряд и ряд, сглаженный методом скользящего среднего

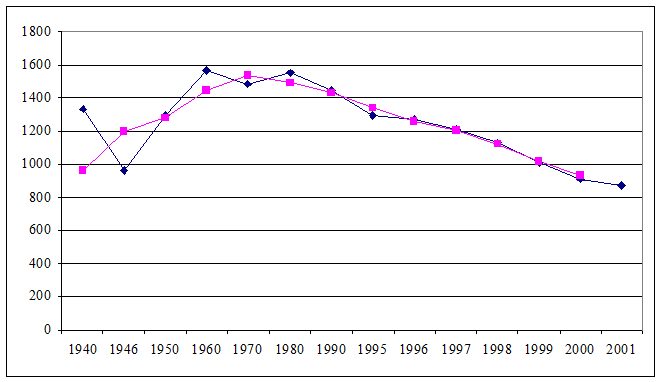4) Оценка автокорреляционной функции.

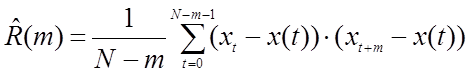
Таблица 3. Таблица значений автокорреляционной функции

Рис. 4 Автоковариационная функция

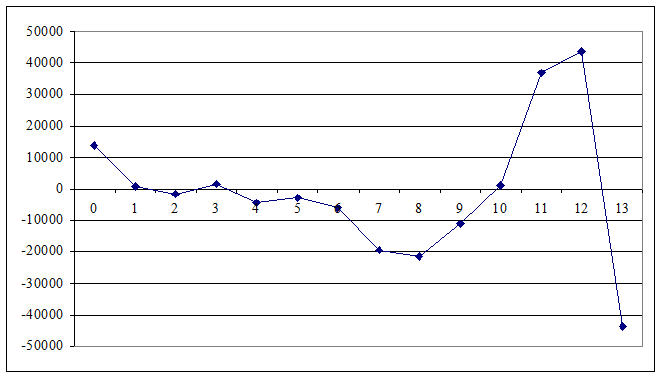
5) Оценим спектральную плотность мощности на основании дискретного преобразования     Фурье:

.

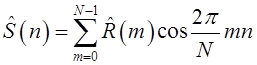Таблица 4. Спектральная плотность

Рис. 5 Спектральная плотность

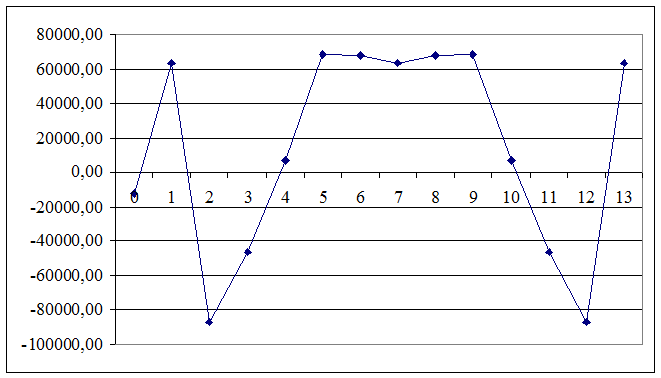
6)  Исходя из найденного тренда, спрогнозируем следующие три члена временного ряда:

.

.

.

.